55

8. Рациональные неравенства.

Всякое рациональное неравенство с параметрами , и переменной имеет область допустимых значений параметров как некоторую часть координатной плоскости. На каждой из них исходное неравенство равносильно неравенству , для некоторых многочленов и с параметрами , и переменной . Пусть -

- разложение этих многочленов в произведение множителей не выше первой и не выше второй степеней. Нулями функции являются общие решения уравнений , точками разрыва - общие решения уравнений .

На множестве всех нулей и точек разрыва функции каждым фиксированным значениям параметров , соответствует некоторое размещение или перестановка. Согласно теореме 13 классификация всех частных рациональных неравенств осуществляется выделением множеств значений параметров для определённой перестановки или размещения нулей и точек разрыва и использования на выделенных множествах метода интервалов.

Общая схема решения.

1. Выделяются критические значения параметров, для которых соответствующие частные неравенства не определены.

2. На области допустимых значений параметров исходное рациональное неравенство приводится к виду , многочлены и разлагаются в произведение сомножителей не выше первой и не выше второй степеней относительно .

3. Осуществляется решение каждого из уравнений , находятся нули функции на множестве . Осуществляется решение каждого из уравнений , находятся точки разрыва функции на множестве .

4. На множестве 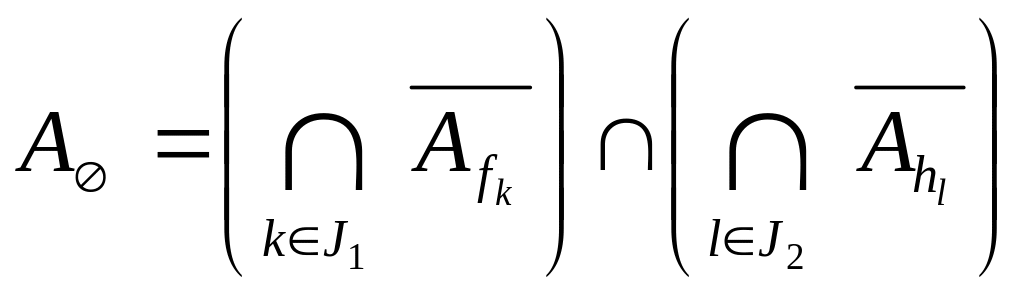всех значений параметров, для которых уравнения и не имеют решений, определяются знаки сомножителей и , множество решений исходного рационального неравенства.

5. Находятся все критические значения параметров, для которых нули (точки разрыва) совпадают с нулями (точками разрыва), то есть обращаются в нуль выражения , , для некоторых общих решений уравнений и 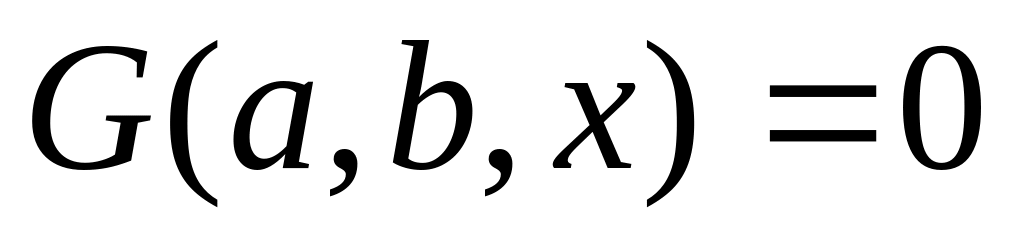. Полученным значениям параметров соответствуют определённые размещения нулей и точек разрыва функции . На каждом из таких множеств осуществляется решение неравенства методом интервалов.

6. На каждом из подмножеств и выделяются фиксированные значения параметров , , для которых , , . Для , определяется перестановка нулей и точек разрыва частной функции . Находится множество значений полученной перестановки как решение системы соответствующих неравенств для нулей и точек разрыва. На выделенных множествах методом интервалов осуществляется поиск общих решений отдельного типа частных неравенств.

9. Иррациональные уравнения.

На области допустимых значений параметров иррациональные уравнения методом равносильных преобразований можно привести к уравнению вида

(1),

которое равносильно системе

(2).

Общая схема решения.

1. На координатной плоскости (числовой прямой, если параметр один) определяется область допустимых значений параметров. Выделяется область определения из условий положительности всех выражений под корнями чётных степеней. Дальнейшее решение осуществляется в этой области.

2. Исходное иррациональное уравнение при помощи равносильных преобразований приводится к виду (1), которое равносильно системе (2).

3. На области допустимых значений параметров исходного иррационального уравнения осуществляется решение уравнения системы (2) по ранее изложенной схеме. Для каждого общего решения уравнения устанавливается множество значений параметров.

4. На множестве находятся все значения параметров, для которых удовлетворяет неравенству , и лежащих в области допустимых значений параметров. На множестве найденных значений параметров является общим решением исходного иррационального уравнения.

5. Для всех общих решений уравнения системы (2) пересечениями множеств и их дополнений определяются все типы частных уравнений.