3. Спектрально-кореляційна теорія стаціонарних дискретних випадкових сигналів

Як випливає із попередніх підрозділів, при дослідженні як в теоретичному, так і в практичному плані дискретних випадкових сигналів бажано знати їх повний теоретико-ймовірнісний опис, тобто випадковий дискретний сигнал буде повністю заданий, якщо відома послідовність його -вимірних розподілів, де , тобто область визначення сигналу містить моментів часу. Але на практиці, не кажучи про великі обсяги обчислень, досить складно не тільки отримати таку послідовність для реальних випадкових сигналів, а навіть аналітично її описати, за винятком, можливо, гауссівської випадкової послідовності. Більше того, для низки практичних задач такий повний вичерпний опис буває і не потрібний. Тому часто обмежуються розглядом частинних характеристик дискретних випадкових сигналів, а саме, початкових та центральних змішаних моментних функцій різних порядків. Так в практиці обробки випадкових сигналів, у тому числі і дискретних, широке застосування отримали моментні функції перших двох порядків: математичне сподівання або середнє випадкового сигналу, дисперсія та кореляційна функція. Як буде показано далі, на основі кореляційної функції стаціонарних випадкових сигналів можна отримати їх енергетичні спектри. Тому аналіз випадкових процесів, в тому числі дискретних, в рамках перших двох моментів отримав назву енергетичної або спектрально-кореляційної теорії випадкових сигналів.

Оскільки в попередніх підрозділах було розглянуто означення математичного сподівання, дисперсії і кореляційної функції і, окрім того, враховуючи, що для практики обробки випадкових сигналів середнє не відіграє у більшості випадків надто великого значення, а дисперсія є частинним випадком кореляційної функції при зсуві , то далі ми будемо розглянемо основні властивості останньої і саме для стаціонарних випадкових дискретних сигналів. Більше того, із двох дискретних сигналів детально зупинимось на спектрально-кореляційному аналізі дискретної випадкової послідовності, оскільки її реалізації можуть розглядатися як цифрові сигнали.

Отже нехай маємо стаціонарну дискретну випадкову послідовність

, , (2.55)

де будемо вважати, що , а кожній точці часової вісі ми маємо одну і ту ж дискретну випадкову величину, яка може набувати можливих значень .

Одновимірний розподіл стаціонарної дискретної послідовності (2.55), потрібний для визначення її середнього і дисперсії, не залежить від часу (див. формулу (2.47)) і задається лише однією табл. 2.3. Тому математичне сподівання, так само як і дисперсія, стаціонарної дискретної послідовності характеризуються одним числовим значенням, тобто математичне сподівання - і дисперсія .

Двовимірний розподіл ймовірностей послідовності (2.55), потрібний для визначення кореляційної функції, залежить від різниці моментів часу (див. формулу (2.50)) і потребує для його опису цілої низки таблиць. Позначимо кількість таких таблиць . Оскільки область визначення дискретної випадкової послідовності (2.55) складається з різних часових точок , то із них можна вибрати

.

різних пар , де . Значить існує і різниць моментів часу . Але оскільки серед цієї множини різниць моментів часу можуть бути і такі, що співпадають за своїм значенням, то для стаціонарної дискретної випадкової послідовності (2.55) існує всього двовимірних розподілів ймовірностей виду (2.50), або, що теж саме, таблиць, подібних до табл. 2.4.

Таблиця 2.4

			…
			…
			…
…	…	…	…	…
			…

Кожна така таблиця дозволяє найти одне із значень кореляційної функції стаціонарної дискретної випадкової послідовності (2.55) за наступною формулою

(2.56)

В формулі (2.56) всі можливі різниці моментів часу із області визначення послідовності (2.55) можна розділити на дві групи. В першу групу включимо ті, для

для яких . В цьому випадку , тобто додатні різниці часу. До другої групи відносяться різниці моментів часу, для яких . В цьому випадку , тобто від’ємні різниці часу. Оскільки в правій частині (2.56) при перестановці співмножників і їх добуток не міняється, а -вимірні розподіли ймовірностей, в тому числі і двовимірні, дискретної випадкової послідовності задовольняють умові симетрії, тобто , то значення кореляційної функції для різних за знаком але однакових за модулем значень її аргументу співпадають, тобто

. (2.57)

Зауважимо тепер, що при формула (2.56) співпадає з формулою для визначення дисперсії, тобто

. (2.58)

Отже, об’єднавши (2.57) і (2.58) та упорядкувавши значення у порядку зростання різниць моментів часу , отримаємо кореляційну функцію стаціонарної дискретної випадкової послідовності

, (2.59)

яка представляє собою дискретну парну, тобто симетричну відносно вісі ординат, функцію, що задовольняє умові

.

На рис. 2.6 зображено один із можливих видів кореляційної функції для деякої стаціонарної дискретної випадкової послідовності , .

Слід зазначити, що згідно з формулою (2.59), у загальному випадку кількість дискретних значень кореляційної функції дорівнює

.

Але така кількість значень буде, коли серед всіх можливих різниць моментів часу

(2.60)

немає однакових. Якщо ж в області визначення стаціонарної дискретно випадкової послідовності зустрічаються такі моменти часу , що, наприклад, , то для них значення кореляційної функції співпадають, тобто . Отже у цьому випадку по суті ми маємо одне значення кореляційної функції і тоді загальна кількість значень кореляційної функції буде меншою числа . Чим більше такого роду співпадань,

Рис. 2.6. Кореляційна функція стаціонарної дискретної

випадкової послідовності

тим меншою буде кількість різних значень дискретної кореляційної функції у порівнянні з кількістю . Позначимо через максимальне значення різниці моментів часу серед усіх можливих різниць (2.60). Тоді всі різні можливі ненульові значення кореляційної функції (2.59) будуть розташовані в межах інтервалу (див. рис. 2.6). Отже «тривалість» кореляційної функції стаціонарної дискретної випадкової послідовності , дорівнює .

Зазначимо ще, що оскільки кореляційна функція стаціонарної випадкової послідовності є парною функцією, то при зображенні її або аналітичному описі досить розглядати лише значення, наприклад, на додатній вісі. На від’ємній ці значення симетрично відносно вісі ординат повторюються (рис. 2.6). Більше того, з практичної точки зору краще розглядати нормовану кореляційну функцію яка носить назву коефіцієнта кореляції, і максимальне значення якої дорівнює 1 при (див рис. 2.7)

Рис. 2.7. Нормована кореляційна функція стаціонарної дискретної

випадкової послідовності

Ми розглянули кореляційну функцію стаціонарної дискретної випадкової послідовності (2.55). Розглядати детально кореляційну функцію стаціонарної випадкової послідовності ми не будемо, оскільки всі її властивості в цілому подібні до розглянутих вище для стаціонарної дискретної випадкової послідовності. Різниця полягає лише в визначенні кореляційної функції стаціонарної випадкової послідовності. Справа в тому, що в цьому випадку розглядається стаціонарна послідовність неперервних випадкових величин , , які описуються щільностями розподілу ймовірностей. Для визначення кореляційної функції потрібна двовимірна щільність

.

І тоді кореляційна функція стаціонарної випадкової послідовності ,

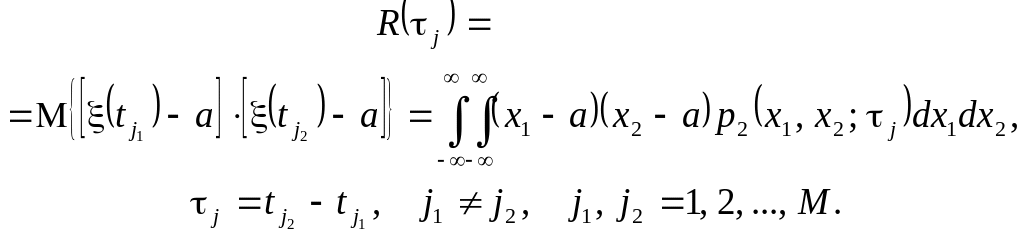
(2.61)

Всі властивості та висновки, особливості зображення кореляційної функції (2.61) співпадають з властивостями та висновками, особливостями зображення кореляційної функції (2.56) повністю співпадають. Тому далі будемо розглядати просто дискретну кореляційну функцію

, (2.62)

не акцентуючи увагу на тому, чи відповідає вона випадковій послідовності, чи дискретній випадковій. При цьому для останніх будемо використовувати, коли це не викличе непорозумінь, загальну назву – дискретний випадковий процес.

Кореляційну функцію (2.62) можна розглядати як дискретну детерміновану функцію, представлену у часовій області. Тоді, згідно з результатами розділу 1, на основі дискретного перетворення Фур’є можна перейти до її зображення у частотній області. Тим самим ми отримаємо спектр відповідного стаціонарного дискретного випадкового процесу. Але оскільки перетворенню Фур’є підлягають не окремі реалізації дискретного випадкового процесу, а кореляційна функція, то ми отримаємо не амплітудний спектр гармонічних складових, спектр потужності, тобто розподіл середньої потужності дискретного випадкового процесу по дискретних частотах.

Перш ніж перейти до розгляду спектру потужності дискретного випадкового процесу, зробимо одно зауваження відносно кореляційної функції (2.62), як деякої дискретної функції. Справа в тому, що ДПФ, яке розглядалось у першому розділі для дискретних сигналів, передбачало, що відліки останнього розташовані еквідістантно. При визначенні ж кореляційної функції (2.62) ми не накладали подібного роду обмежень на розташування відліків на вісі часу. Тому для ДПФ кореляційної функції традиційна форма запису повинна бути дещо змінена. Зупинимось на цьому питанні детальніше.

Нехай маємо дві дискретні послідовності (рис. 2.8), одна з яких

Рис. 2.8. Еквідістантна а) і нееквілістантна б) детерміновані

часові послідовності

є еквідістантною (рис. 2.8, а)

, (2.62)

а інша – нееквідістантна (рис. 2.8, б)

, (2.63)

де - послідовність часових інтервалів, на які зсунуті відповідні відліки еквідістантної послідовності (2.62). Такі зсуви можуть бути додатні (зсув вправо), від’ємні (зсув вліво) або нульові (зсув відсутній). (УТОЧНИТИ ПОДАЛЬШИЙ РОЗГЛЯД ПРИ НЕУКВІДІСТАНТНИХ ВІДЛІКАХ) ?

Розглянемо випадок, коли дискретна кореляційна функція має еквідістантні відліки, тобто

. (2.64)

Знайдемо дискретне перетворення Фур’є кореляційної функції (2.64). Оскільки кореляційна функція є парною функцією, то, по-перше, перетворення Фур’є є дійсною функцією дискретної частоти, а по-друге, двохстороннє перетворення

,

можна записати у вигляді одностороннього ДПФ:

, . (2.65)

Обернене до (2.65) перетворення Фур’є запишемо так:

, . (2.66)

Таким чином, двійка ДПФ (2.65) і (2.66) пов’язують між собою кореляційну функцію і спектр потужності стаціонарного дискретного випадкового сигналу , .????

Дисперсія стаціонарного дискретного випадкового сигнал , тому на основі співвідношення (2.66) отримуємо

.

Це означає, що дисперсія дискретного процесу дорівнює сумі потужностей всіх складових його дискретного спектру.

Оскільки кореляційна функція і спектр потужності пов’язані двійкою перетворень Фур’є (2.65) і (2.66), то для них є характерним обернене ний зв’язок між «швидкостями» спадання значень складових кореляційної функції і спектру потужності з ростом їх номера. Так, чим повільніше спадають значення кореляційної функції, тим швидше спадають складові спектру потужності, і навпаки.

52