
2. Випадкові дискретні сигнали
В попередньому розділі ми розглянули детерміновані дискретні сигнали та їх перетворення. Але слід зауважити, що реальні сигнали в системах обробки інформації взагалі і в системах ЦОС зокрема мають випадковий характер. Дійсно, по-перше, сигнал, що містить в собі інформацію, повинен мати в тій чи іншій мірі деяку степінь невизначеності, тобто випадковості. Сигнал, про який все відомо, не несе в собі ніякої корисної інформації. По-друге, на корисні сигнали завжди накладаються різноманітного роду завади та шуми, які теж є випадковими.
Математичною моделлю випадкових сигналів є випадкові процеси. Тому в цьому розділі розглядаються загальне означення випадкових процесів, їх класифікація. Описуються теоретико-ймовірнісні характеристики дискретних випадкових процесів, а саме розподіли ймовірностей, функції розподілу та щільності розподілу ймовірностей, числові характеристики, зокрема, математичне сподівання, дисперсія, кореляційна функція. Більш детально розглядаються дискретні стаціонарні випадкові процеси та їх спектрально-кореляційна теорія.
2.1. Означення випадкових процесів та їх класифікація
На
відміну від випадкової величини
![]() ,
яка є функцією одної змінної
,
яка є функцією одної змінної
![]() ,
де
,
де
![]() - простір елементарних подій, випадковий
процес
- простір елементарних подій, випадковий
процес
![]() є функцією двох змінних: елементарної
події
і дійсної змінної
є функцією двох змінних: елементарної
події
і дійсної змінної
![]() ,
де
,
де
![]() - область визначення процесу, яку частіш
за все на практиці інтерпретують як
час. Іншими словами, випадковий процес
можна розглядати як випадкову величину,
яка «розвивається» у часі.
- область визначення процесу, яку частіш
за все на практиці інтерпретують як
час. Іншими словами, випадковий процес
можна розглядати як випадкову величину,
яка «розвивається» у часі.
Кожна змінна випадкового процесу відіграє свою роль. Елементарна подія визначає випадковий характер процесу, вірніше, та ймовірність, яка приписується елементарній події. Часова змінна, яку часто вважають параметром, визначає характер розвитку процесу у часі.
Якщо
зафіксувати деякий момент часу
![]()
![]() ,
то ми отримаємо переріз
або
значення
випадкового процесу
,
то ми отримаємо переріз
або
значення
випадкового процесу
![]() в момент часу
в момент часу
![]() .
Оскільки час зафіксовано, то часова
змінна як би зникає і переріз випадкового
процесу буде представляти собою випадкову
величину
.
Оскільки час зафіксовано, то часова
змінна як би зникає і переріз випадкового
процесу буде представляти собою випадкову
величину
![]() .
Звідси можна дати інше означення.
Випадковий процес
- це упорядковане за параметром
сімейство випадкових величин
.
Звідси можна дати інше означення.
Випадковий процес
- це упорядковане за параметром
сімейство випадкових величин
![]() .
.
Якщо ж
зафіксувати елементарну подію
![]() ,
то «зникає» випадковість і ми отримаємо
детерміновану функцію часу
,
то «зникає» випадковість і ми отримаємо
детерміновану функцію часу
![]() ,
яка носить назву реалізації
(траєкторії)
випадкового процесу.
На цій основі можна дати ще одне означення
випадкового процесу: це деяка множина
функцій часу
,
яка носить назву реалізації
(траєкторії)
випадкового процесу.
На цій основі можна дати ще одне означення
випадкового процесу: це деяка множина
функцій часу
![]() (2.1)
(2.1)
з заданою на ній імовірнісною мірою.
В
співвідношенні (2.1) елементарна подія
![]() ,
записана у вигляді індексу, може
розглядатися як деякий „номер”
реалізації випадкового процесу. В
залежності від виду простору елементарних
подій
,
„номер” реалізації випадкового процесу,
а значить і кількість його реалізацій,
може набувати скінченої, зліченої або
континуальної множини значень. На рис.
2.1. зображено три реалізації
,
записана у вигляді індексу, може
розглядатися як деякий „номер”
реалізації випадкового процесу. В
залежності від виду простору елементарних
подій
,
„номер” реалізації випадкового процесу,
а значить і кількість його реалізацій,
може набувати скінченої, зліченої або
континуальної множини значень. На рис.
2.1. зображено три реалізації
![]() випадкового процесу
випадкового процесу
![]() .
Зазначимо, що, на відміну від випадкового
процесу, будь-який детермінований процес
.
Зазначимо, що, на відміну від випадкового
процесу, будь-який детермінований процес
![]() має лише одну реалізацію. Для останнього
його розвиток у часі апріорі визначений
однозначно, тобто у будь-який момент
часу
ми можемо однозначно вказати значення,
якого набуде детермінований процес
має лише одну реалізацію. Для останнього
його розвиток у часі апріорі визначений
однозначно, тобто у будь-який момент
часу
ми можемо однозначно вказати значення,
якого набуде детермінований процес
![]() .
Для випадкового ж процесу визначити
апріорі конкретне значення, якого він
набуде у момент часу
неможливо. Можна лише вказати імовірність
того,
.
Для випадкового ж процесу визначити
апріорі конкретне значення, якого він
набуде у момент часу
неможливо. Можна лише вказати імовірність
того,
що в момент часу реалізація процесу буде лежати, в
T![]()

Рис. 3.1. Реалізації випадкового процесу
межах
від
![]() до
до
![]() ,
тобто
,
тобто
![]() ,
де
,
де
![]() позначає ймовірність випадкової події,
вказаної в фігурних дужках.
позначає ймовірність випадкової події,
вказаної в фігурних дужках.
Приклад 3.1. Наведемо декілька прикладів випадкових процесів.
Зміна у часі температури повітря у фіксованій точці навколишнього середовища протягом доби.
Зміна висоти польоту літака за час його прольоту над деякими точками
 і
і
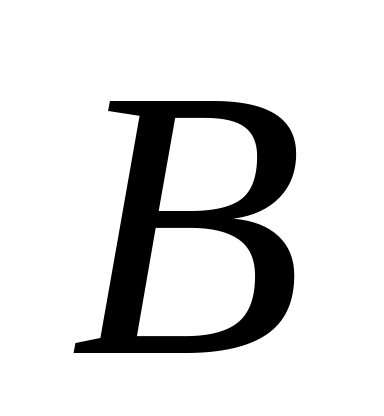 ,
що розташовані на поверхні землі.
,
що розташовані на поверхні землі.Залежність напруги на виході приймальної антени від часу за деякий фіксований його проміжок.
Кількість заявок, що надходять на станцію технічного обслуговування за одну годину, на протязі доби.
Кількість пшениці, що збирається кожен рік в Україні, в залежності від області.
Зміна у часі однієї із координат броунівської частинки при її переміщенні у розчині за фіксований інтервал часу.
Артеріальний тиск у людини на протязі доби.∙
Далі,
для спрощення записів, ми будемо позначати
випадковий процес символом
![]() ,
не вказуючи залежність його від
елементарної події
,
але маючи це на увазі. Окрім того
зазначимо, що значення (або реалізації)
випадкової величини
позначають літерою
,
не вказуючи залежність його від
елементарної події
,
але маючи це на увазі. Окрім того
зазначимо, що значення (або реалізації)
випадкової величини
позначають літерою
![]() (з індексом або без нього). Для збереження
аналогії далі будемо позначати реалізації
випадкового процесу
(з індексом або без нього). Для збереження
аналогії далі будемо позначати реалізації
випадкового процесу
![]() функцією
функцією
![]() з відповідним індексом, що вказує номер
реалізації, або без нього, якщо в цьому
не буде потреби.
з відповідним індексом, що вказує номер
реалізації, або без нього, якщо в цьому
не буде потреби.
Множину
значень
часової змінної
![]() називають областю
означення
випадкового процесу
.
називають областю
означення
випадкового процесу
.
Множина
![]() усіх тих значень, яких можуть набувати
реалізації випадкового процесу
,
називається простором
значень процесу
або його фазовим
простором.
усіх тих значень, яких можуть набувати
реалізації випадкового процесу
,
називається простором
значень процесу
або його фазовим
простором.
Одну із можливих класифікацій випадкових процесів можна здійснити на основі того, який характер носять область означення та фазовий простір випадкового процесу.
Дискретна випадкова послідовність (дискретний процес з дискретним часом). Це випадковий процес , у якого і фазовий простір , і область означення є дискретними (скінченими або зліченими) множинами:
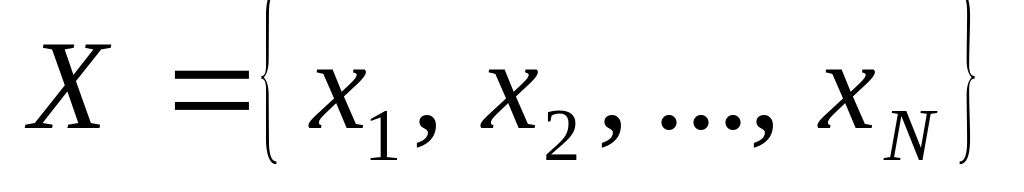 ,
,
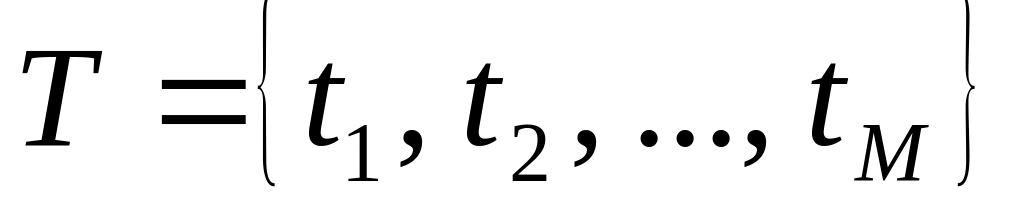 ,
де
,
де
 і
і
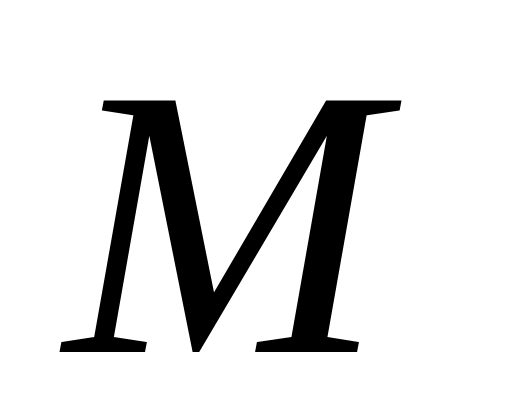 обидва,
або один із них, можуть прямувати і до
обидва,
або один із них, можуть прямувати і до
 Такий випадковий процес є найпростішим
процесом. Його можна розглядати як
випадкову
-вимірну
векторну величину
Такий випадковий процес є найпростішим
процесом. Його можна розглядати як
випадкову
-вимірну
векторну величину
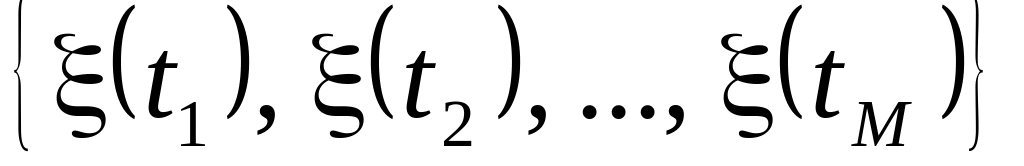 ,
компоненти якої є дискретними випадковими
величинами і можуть набувати значень
із
,
компоненти якої є дискретними випадковими
величинами і можуть набувати значень
із
 .
Такий процес повністю можна описати
за допомогою
-вимірного
розподілу імовірностей або
-вимірної
дискретної сумісної функції розподілу
ймовірностей, що буде розглянуто у
підрозділі 2.2. Для реальних дискретних
випадкових послідовностей фазовий
простір
і область означення
є скінченими множинами. При цьому перша
множина може містити як додатні, так і
від’ємні числа, а друга – лише невід’мні.
Кількість реалізацій такого процесу
обмежена і дорівнює добутку
.
Такий процес повністю можна описати
за допомогою
-вимірного
розподілу імовірностей або
-вимірної
дискретної сумісної функції розподілу
ймовірностей, що буде розглянуто у
підрозділі 2.2. Для реальних дискретних
випадкових послідовностей фазовий
простір
і область означення
є скінченими множинами. При цьому перша
множина може містити як додатні, так і
від’ємні числа, а друга – лише невід’мні.
Кількість реалізацій такого процесу
обмежена і дорівнює добутку
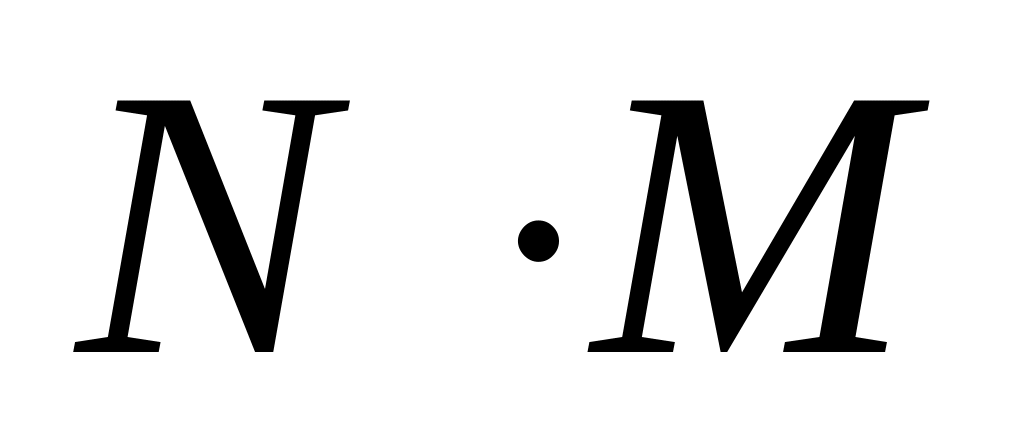 .
Це означає, що ймовірність появи кожної
з таких реалізацій задовольняє нерівності
.
Це означає, що ймовірність появи кожної
з таких реалізацій задовольняє нерівності
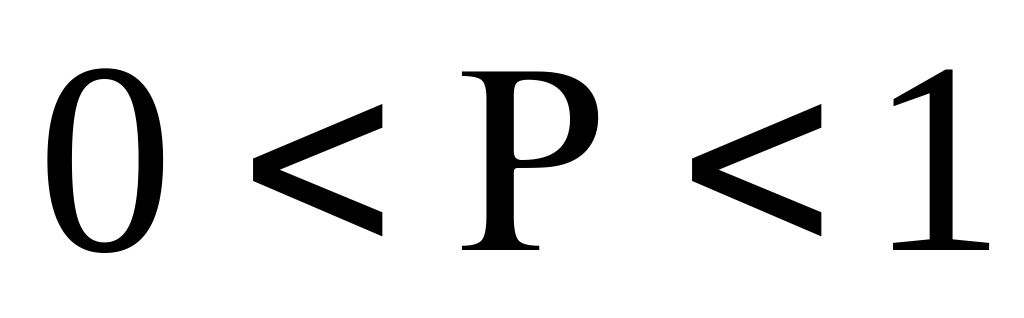 ,
тобто є ненульовою.
,
тобто є ненульовою.
Одна із
можливих реалізацій
![]() такого процесу зображена на рис. 2.2.
такого процесу зображена на рис. 2.2.
0
…
…
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 2.2. Реалізація дискретної випадкової послідовності
Випадкова послідовність (неперервний процес з дискретним часом). Для такого процесу фазовий простір є деяким відрізком числової вісі (континуум), тобто
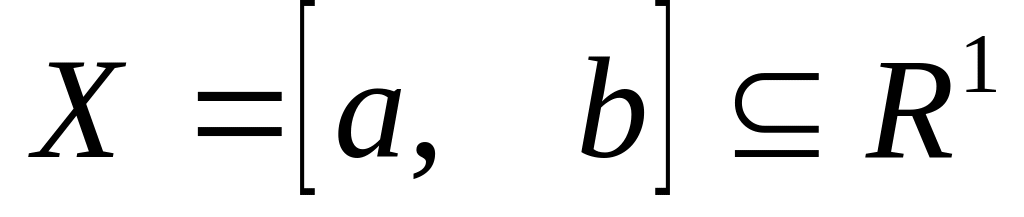 ,
а область означення – дискретна множина
,
де
може бути скінченим, а може прямувати
і до
,
а область означення – дискретна множина
,
де
може бути скінченим, а може прямувати
і до
 .
Цей процес теж можна розглядати як
-вимірний
випадковий вектор
,
у якого складові є неперервними
випадковими величинами. Імовірнісні
властивості таких процесів повністю
характеризуються відповідними
-вимірними
сумісними функціями або щільностями
розподілу ймовірностей, що буде
детальніше розглянуто в підрозділі
2.3. Отже, для випадкових послідовностей
область означення подібна до області
означення дискретних випадкових
послідовностей. Фазовий же простір
представляє собою незлічену множину.
Тому множина реалізацій будь-якої
випадкової послідовності теж представляє
собою незлічену множину. А це в свою
чергу означає, що ймовірність появи
конкретної реалізації дорівнює нулеві.
.
Цей процес теж можна розглядати як
-вимірний
випадковий вектор
,
у якого складові є неперервними
випадковими величинами. Імовірнісні
властивості таких процесів повністю
характеризуються відповідними
-вимірними
сумісними функціями або щільностями
розподілу ймовірностей, що буде
детальніше розглянуто в підрозділі
2.3. Отже, для випадкових послідовностей
область означення подібна до області
означення дискретних випадкових
послідовностей. Фазовий же простір
представляє собою незлічену множину.
Тому множина реалізацій будь-якої
випадкової послідовності теж представляє
собою незлічену множину. А це в свою
чергу означає, що ймовірність появи
конкретної реалізації дорівнює нулеві.
Реалізація одного з таких процесів зображена на рис. 2.3.
0
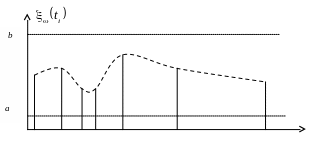

![]() . . .
t
. . .
t
Рис. 2.3. Реалізація випадкової послідовності
Дискретний (розривний) випадковий процес (дискретний процес з неперервним часом). Для цього процесу фазовий простір є дискретною множиною
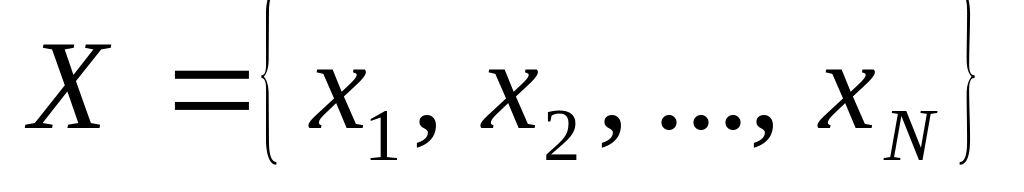 ,
де
може прямувати і до нескінченності, а
область означення – неперервна
(континуальна) множина
,
де
може прямувати і до нескінченності, а
область означення – неперервна
(континуальна) множина
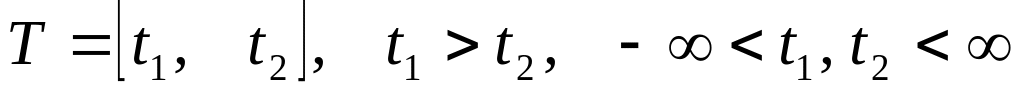 .
Такі процеси можна описувати за допомогою
багатовимірних розподілів або
багатовимірних дискретних функцій
розподілу імовірностей, але цей опис
буде неповний. Можна лише стверджувати,
що чим більша розмірність розподілу,
тим детальніший буде опис. Причина цієї
проблеми полягає в тому, що область
означення
.
Такі процеси можна описувати за допомогою
багатовимірних розподілів або
багатовимірних дискретних функцій
розподілу імовірностей, але цей опис
буде неповний. Можна лише стверджувати,
що чим більша розмірність розподілу,
тим детальніший буде опис. Причина цієї
проблеми полягає в тому, що область
означення
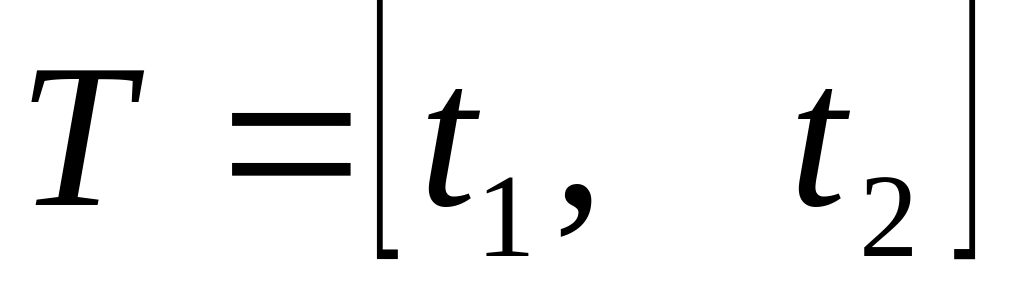 процесу є незліченою множиною і навіть
нескінченновимірний розподіл не
охарактеризує поведінку процесу у всіх
точках інтервалу
.
Винятком для таких процесів є так звані
сепарабельні процеси, для яких у
континуальній множині
існує злічена кругом щільна підмножина
процесу є незліченою множиною і навіть
нескінченновимірний розподіл не
охарактеризує поведінку процесу у всіх
точках інтервалу
.
Винятком для таких процесів є так звані
сепарабельні процеси, для яких у
континуальній множині
існує злічена кругом щільна підмножина
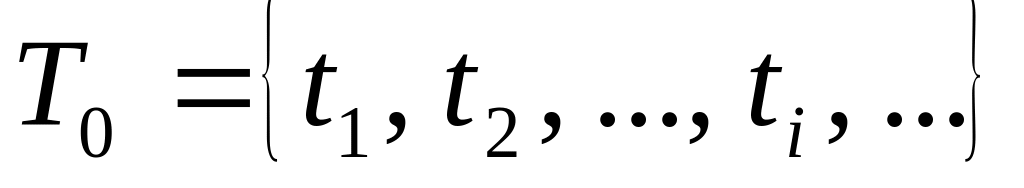 ,
в точках якої значення процесу повністю
його характеризують. Тобто, іншими
словами, сепарабельний випадковий
процес може бути повністю відновлений
на всій континуальній множині
за його значеннями на зліченій множині
.
,
в точках якої значення процесу повністю
його характеризують. Тобто, іншими
словами, сепарабельний випадковий
процес може бути повністю відновлений
на всій континуальній множині
за його значеннями на зліченій множині
.
Приклад реалізації дискретного випадкового процесу наведено на рис. 2.4.

Рис. 2.4. Реалізація дискретного випадкового процесу
4. Неперервний випадковий процес. Для такого процесу неперервними є і його фазовий простір , і область визначення , тобто , а . Відносно теоретико-імовірнісного опису таких процесів можна сказати те ж саме, що і для дискретних випадкових процесів, які розглядалися у п. 3. Відмінністю є лише те, що неперервні випадкові процеси описуються неперервними багатовимірними функціями розподілу, а значить для них існують і багатовимірні сумісні щільності розподілу імовірностей. Одна з можливих реалізацій неперервного випадкового процесу наведена на рис. 2.5.

Рис. 2.5. Реалізація неперервного випадкового процесу
Наведена класифікація випадкових процесів звичайно далеко не вичерпує всіх можливих способів їх класифікації і існуючих класів. Так, можна класифікувати процеси за видами розподілів, якими описуються їх теоретико-імовірнісні характеристики. Відомий, наприклад, широкий клас гауссівських процесів, які описуються нормальними розподілами. В залежності від виду стохастичної залежності значень випадкових процесів останні поділяються на корельовано і некорельовані процеси, процеси типу білого шуму, процеси з незалежними приростами, марківські процеси, мартінгали. Поділяють також процеси за особливостями залежності параметрів та послідовностей розподілів імовірностей випадкових процесів від часу на нестаціонарні і стаціонарні. Останні, в свою чергу, можна розділити за видом їх енергетичних спектрів на широкосмужні і вузькосмужні. Останнім часом все більш широкого застосування в практиці статистичної обробки сигналів знаходять так звані безмежно подільні випадкові процеси і їх підклас – лінійні випадкові процеси. Це широкий клас процесів, які описуються граничними або безмежно подільними розподілами. Сюди відносяться і такі, добре відомі розподіли, як нормальний, логарифмічно-нормальний, пуассонівський, гамма-розподіл, розподіл Коші та інші. Деякі з видів вказаних типів процесів будуть розглянуті детальніше в подальших підрозділах книги.
Оскільки в системах ЦОС використовуються сигнали з дискретним часом, то далі розглянемо більш детальний теоретико-ймовірнісний опис процесів двох перших класів: дискретні випадкові послідовності (дискретні процеси з дискретним часом) і випадкові послідовності (неперервні процеси з дискретним часом).
