3. Стаціонарні дискретні випадкові сигнали

Як було зазначено на початку цього розділу, математичною моделлю випадкових сигналів є випадкові процеси. Серед випадкових процесів, в тому числі і дискретних випадкових процесів, виділяють клас стаціонарних процесів, які служать математичною моделлю стаціонарних випадкових сигналів. Теоретико-ймовірнісні характеристики стаціонарних процесів інваріантні відносно зсуву реалізацій у часі. Іншими словами, для таких процесів точка початку координат на часовій вісі може бути вибрана довільно. Це не впливає на значення параметрів стаціонарних процесів.

Серед основних причин, які обумовлюють виділення класу стаціонарних процесів можна вказати такі:

1. Теоретико-ймовірнісний аналіз як власне стаціонарних сигналів, так і їх перетворень різного типу системами обробки інформації значно простіший у порівнянні з аналізом нестаціонарних процесів, що буде зрозуміло із подальшого розгляду.

2. До стаціонарних процесів можуть бути застосовані методи спектрального аналізу, подібно до того, як це було розглянуто в розділі 1 для детермінованих сигналів.

3. Серед реальні сигнали, що використовуються в системах ЦОС, значна їх кількість може бути досить адекватно описана за допомогою класу стаціонарних процесів.

4. Дослідження статистичних даних, отриманих в рамках моделі стаціонарних випадкових сигналів виконуються з меншими затратами як часових ресурсів, так і фінансових.

Розглянемо означення та основні характеристики стаціонарних дискретних процесів. Почнемо розгляд з дискретної випадкової послідовності, яка представляє собою упорядковану у часі послідовність дискретних випадкових величин

, (2.43)

заданих на одному і тому ж просторі елементарних подій і які мають один і той же фазовий простір .

Якщо для будь-якого цілого додатного , будь-яких моментів часу із області визначення дискретної випадкової послідовності (2.43) і будь-якого для -вимірної сумісної функції розподілу послідовності (2.43) виконується співвідношення

(2.44)

то дискретна випадкова послідовність називається стаціонарною (або стаціонарною у вузькому розумінні).

Рівність (2.44) є необхідною і достатньою умовою стаціонарності дискретної випадкової послідовності, тобто, для того, щоб послідовність (2.43) була стаціонарною, необхідно виконання умови (2.44). І навпаки, якщо умова (2.44) виконується, то послідовність (2.43) є стаціонарною.

Для стаціонарної у вузькому розумінні дискретної випадкової послідовності рівність, подібна до (2.44) , виконується і для розподілу ймовірностей, а саме

,

, (2.45)

де - кількість можливих значень дискретних випадкових величин послідовності (2.43), яка може прямувати і до нескінченності.

Оскільки за означенням значення може бути вибрано довільно, то поклавши його в (2.44) (або в (2.45)) рівним , отримаємо

(2.46)

де

.

Таким чином, із (2.46) випливає, що для стаціонарного процесу -вимірна функція розподілу залежить не від моментів часу, від -1.

Аналогічний результат можна отримати і для розподілу ймовірностей

,

,

Зокрема, якщо , то для одновимірних розподілів ймовірностей маємо

. (2.47)

Отже, одновимірний розподіл ймовірностей для стаціонарної дискретної випадкової послідовності не залежить від часу, а це означає, що всі випадкові величини в послідовності (2.43) мають один і той же розподіл. І тоді табл. 2.1 набуває простого вигляду

Таблиця 2.3

			…
			…

Звичайно, для розподілу (2.47) виконується умова

.

Від часового параметра не буде залежати і одновимірна функція розподілу стаціонарного процесу

. (2.48)

На відміну від співвідношень (2.44) і (2.45), співвідношення (2.47) і (2.48) є необхідними але не достатніми для стаціонарності дискретної випадкової послідовності у вузькому розумінні. Тобто виконання останніх співвідношень не гарантує стаціонарності послідовності.

Оскільки на основі одновимірного розподілу ймовірностей знаходяться математичне сподівання і дисперсія дискретної випадкової послідовності, то для стаціонарного процесу вони теж не будуть залежати від часу, тобто

і

Для випадку, коли =2, співвідношення (2.46) запишеться у такому вигляді:

(2.49)

Таким чином, двовимірна функція розподілу стаціонарної дискретної випадкової послідовності залежить не від двох моментів часу і , а від їх різниці .

Аналогічна властивість буде виконуватися і для двовимірного розподілу ймовірностей, тобто

, ,

(2.50)

Звідси кореляційна функція (2.13) стаціонарної дискретної випадкової послідовності теж залежить не від двох моментів часу і , а від їх різниці , а саме

Співвідношення (2.49) і (2.50) теж є необхідними але не достатніми для стаціонарності дискретної випадкової послідовності у вузькому розумінні.

Окрім розглянутого класу стаціонарних у вузькому розумінні дискретних випадкових послідовностей у практиці ЦОС розглядається більш широкий клас слабо стаціонарних (або стаціонарних у широкому розумінні) дискретних випадкових послідовностей.

Дискретних випадкова послідовність , називається слабо стаціонарною або стаціонарною у широкому розумінні якщо її математичне сподівання не залежить від часу

а кореляційна функція залежить від різниці моментів часу

Тут слід зауважити, що із стаціонарності дискретної випадкової послідовності випливає її стаціонарність у широкому розумінні. Обернене твердження у загальному випадку невірне.

Окрім того, із означення випливає, що для стаціонарності у широкому розумінні необхідною і достатньою умовою є виконання співвідношень (2.47) і (2.49) або, що є еквівалентним, співвідношень (2.48) і (2.49). На відміну від необхідних і достатніх умов стаціонарності у вузькому розумінні (2.44) (або (2.45)), справедливість яких на практиці перевірити у більшості випадків неможливо, виконання необхідних і достатніх умов для стаціонарності у широкому розумінні може бути встановлено для реальних дискретних випадкових сигналів. Все це обумовлює той факт. Що на практиці більш широко застосовується поняття слабкої стаціонарності дискретної випадкової послідовності. Тому в подальшому, якщо не буде оговорено окремо, ми під словом стаціонарність будемо розуміти стаціонарність у широкому розумінні.

В цьому підрозділі ми розглянули стаціонарні дискретні випадкові послідовності, задані в дискретні моменти часу на всій числовій вісі, тобто Але в системах ЦОС розглядаються дискретні випадкові послідовності, задані на обмеженому інтервалі часу: , . Для таких послідовностей, строго кажучи, означення стаціонарності (див. формули (2.44), (2.45)) не може бути застосоване. Тому будемо вважати, що дискретна випадкова послідовність , є відрізком стаціонарної дискретної випадкової послідовності , якщо їх значення в моменти часу співпадають. Таку дискретну випадкову послідовність вважатимемо стаціонарною, для якої виконуються усі розглянуті вище властивості. Таке означення є виправданим, якщо врахувати, що стаціонарна дискретна випадкова послідовність представляє собою по суті послідовність , яка складається із однієї і тієї ж випадкової величини, яка розглядається у різні моменти дискретного часу. Такі ж зауваження можуть бути зроблені і відносно стаціонарності дискретної випадкової послідовності , у широкому розумінні. Зокрема, для такої послідовності кореляційна функція, записана в матричному вигляді буде мати такий вид:

,

де і враховано, що .

Нормована кореляційна функція або коефіцієнт кореляції для дискретної випадкової послідовності , запишеться так

.

Звідси випливає, що між нормованою кореляційною матрицею

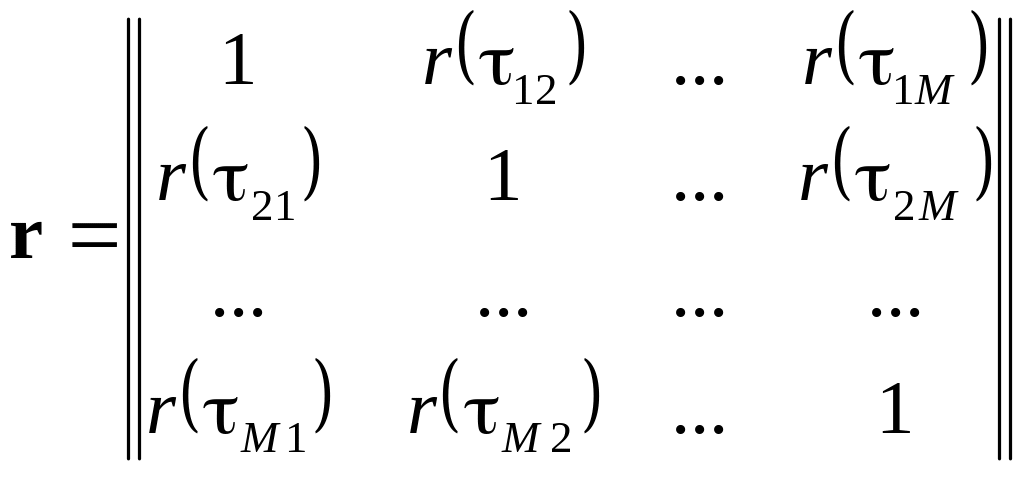
і кореляційною матрицею існує співвідношення

.

Властивість стаціонарності дискретної випадкової послідовності обумовлює певні особливості і для дискретних ланцюгів Маркова. Справа в тому, що для стаціонарної дискретної випадкової послідовності умовна ймовірність

Таким чином, для стаціонарної дискретної випадкової послідовності умовні ймовірності залежать не від двох моментів часу і , а від їх різниці . Тоді для ланцюга Маркова, в основі якого лежить стаціонарна дискретна випадкова послідовність перехідні ймовірності теж будуть залежати лише від різниці моментів часу, а саме, між майбутнім моментом часу і теперішнім часом , тобто

,

.

Розглянемо тепер стаціонарні випадкові послідовності. Різниця між дискретною випадковою послідовністю

(2.51)

і випадковою послідовністю

(2.52)

полягає в тому, що в (2.51) розглядається послідовність дискретних випадкових величин, а в (2.52) – послідовність неперервних випадкових величин. Різниця між дискретними і неперервними випадковими величинами полягає в тому, для перших їх можливі значення утворюють скінчену або зліченну множину, а для других – континуальну множину. Тому дискретні випадкові величини характеризують розподілом ймовірностей або функцією розподілу ймовірностей, а неперервні випадкові величини щільністю розподілу ймовірностей або функцією розподілу ймовірностей. Отже означення стаціонарності в рамках функцій розподілу будуть формально співпадати для (2.51) і (2.52). Тому розглянемо означення стаціонарної випадкової послідовності в рамках щільності розподілу.

Отже випадкова послідовність (2.52) називається стаціонарною у вузькому розумінні, якщо для будь-якого цілого додатного , будь-яких моментів часу із області її визначення і будь-якого для -вимірної сумісної щільності розподілу ймовірностей виконується тотожність

(2.53)

.

З означення (2.53) випливає, що для стаціонарної випадкової послідовності -вимірна щільність розподілу залежить лише від моментів часу

(2.54)

.

Якщо в (2.54) покласти , то отримаємо співвідношення для одновимірної щільності розподілу

,

Отже одновимірна щільність розподілу стаціонарної випадкової послідовності не залежить від часу. А це означає що стаціонарна послідовність (2.52) складається з однієї і тієї ж випадкової величини. Значить від часу не будуть залежати і математичне сподівання і дисперсія стаціонарної випадкової послідовності.

Співвідношення (2.54) для виглядає так

Тобто, двовимірна щільність розподілу ймовірностей стаціонарної випадкової послідовності залежить не від двох моментів часу і , а від їх різниці . Наслідком цього є те, що кореляційна функція стаціонарної випадкової послідовності теж залежить лише від різниці , тобто

Означення слабо стаціонарної або стаціонарної в широкому розумінні випадкової послідовності співпадає з аналогічним означенням для дискретної випадкової послідовності. Формальна різниця полягає лише в тому, що в визначенні математичного сподівання і кореляційної функції для випадкової послідовності використовуються одновимірна і двовимірна щільності розподілу ймовірностей відповідно.

При визначенні дискретного процесу Маркова на основі стаціонарної випадкової послідовності перехідні щільності розподілу ймовірностей теж будуть залежати лише від різниці моментів часу

.

Звідси рівнянню Колмогорова-Чепмена для трьох значень випадкової послідовності , , , де і запишеться у такому вигляді

Для повного теоретико-ймовірнісного опису відрізку стаціонарного дискретного процесу Маркова потрібні перехідні щільності ймовірностей , що залежать лише від різниці моментів часу, і початкова щільность ймовірностей , яка не залежить від часу. Отже -вимірна щільність ймовірностей

.

Іншими словами, для такого дискретного процесу Маркова ймовірність переходу із деякого інтервалу станів в момент часу в інтервал станів в момент часу залежить не від місця розташування цих часових моментів на вісі часу, а від різниці між ними . Це означає, що вибір початку координат на вісі часу для стаціонарного дискретного процесу Маркова не має значення.