Переформулировка в терминах пси-функции Чебышева

Общим начальным этапом рассуждений является переформулировка закона распределения простых чисел в терминах пси-функции Чебышева (англ.), определяемой как

иными словами, пси-функция Чебышева это сумма функции Мангольдта (англ.):

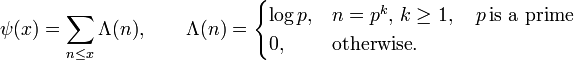
А именно, оказывается, что асимптотический закон распределения простых чисел равносилен тому, что

Это происходит из-за того, что логарифм «почти постоянен» на большей части отрезка  , а вклад квадратов, кубов, и т. д. в сумму (*) пренебрежимо мал; поэтому практически все складываемые логарифмы   примерно равны  , и функция   асимптотически ведёт себя так же, как  .

Проблема о простых числах «близнецах». А. А. Русаков, мггу им. М.А. Шолохова

 Нет ничего сильнее жажды познания, силы сомнения...

В.И.Вернадский

Напомним, натуральное число p , называется простым, если оно имеет ровно два натуральных делителя. Первое простое число 2.

Теорема. Существует бесконечно много простых чисел.

Существует несколько доказательств данной теоремы. Приведём доказательство Евклида.

Доказательство. (Евклид). Допустим, что 2, 3, 4,…, p – множество всех простых чисел и p – наибольшее из них. Рассмотрим целое число (число Евклида)

q = ( ) + 1

Это число не делится ни на одно простое число до p включительно. Но q > 1 и тогда q или само простое число, большее p , или оно делится на простое число, большее p . В обоих случаях существует простое число, большее p . Противоречие, наше предположение неверно. Следовательно, простых чисел бесконечно много.

Если p и p +2 ,- простые числа, то пару чисел ( p ; p +2 ) называют парой простых чисел близнецов.

Упражнение. Первые две пары простых чисел близнецов

(3; 5) и (5; 7) имеют общий элемент (5).

«Расстояние» между второй и третьей парой простых чисел близнецов

(11; 13) равно 11 – 7 = 4.

«Расстояние» между третьей и четвертой (17;19)

17 – 13 = 4,

между четвертой и пятой (29; 31)

29 – 19 = 10.

Теорема Дирихле о простых числах в арифметической прогрессии

Теорема Дирихле о простых числах в арифметической прогрессии гласит:

Каждая арифметическая прогрессия, первый член и разность которой — натуральные взаимно простые числа, содержит бесконечное число простых чисел.

Фактически Дирихле доказал в 1839 году, что при любых фиксированных натуральных взаимно простых числах   и  :

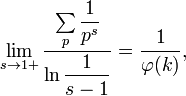
где суммирование ведётся по всем простым числам   с условием  , а   — функция Эйлера.

Это соотношение можно интерпретировать как закон равномерного распределения простых чисел по классам вычетов  , поскольку

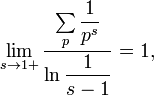
если суммирование ведётся по всем простым числам.