15. Модель емкости с изменяющимся уровнем

Пусть требуется построить модель для емкости, в которую подается жидкость и из которой вытекает жидкость. Входной переменной пусть будет расход на входе, а выходной уровень жидкости в емкости.

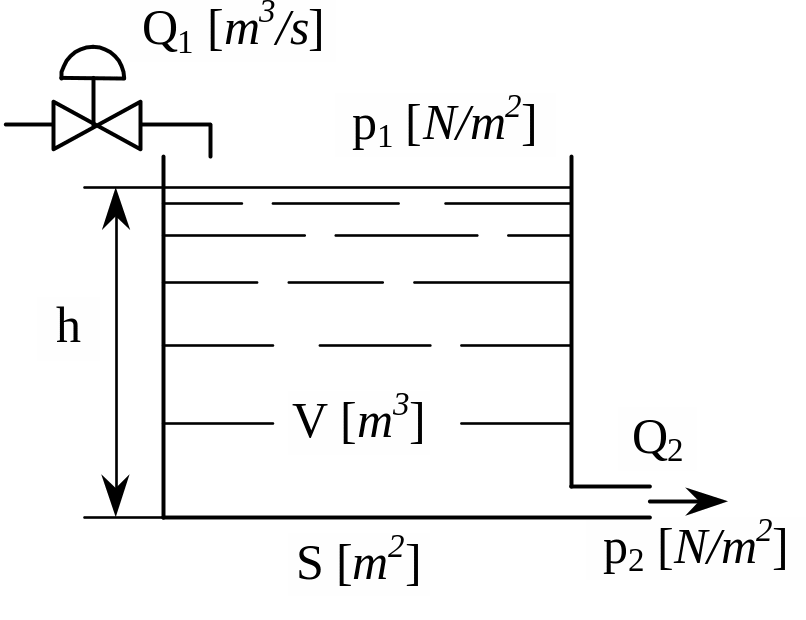
Рис. 15. Емкость с меняющимся уровнем

Материальный баланс в данном случае может быть сведен к следующему:

изменение объема жидкости за время dt равно разности объемов втекающей и вытекающей жидкости, т.е.

dV = Q₁ dt  Q₂ dt

или

dV/dt = Q₁  Q₂.

Объем жидкости в емкости V = S h; откуда

Истечение жидкости из емкости описывается уравнением Бернулли:

где

v  скорость истечения из сливного отверстия,

v₀  скорость изменения уровня в резервуаре,

h  h₀  перепад высот,

p₁, p₂  давление над жидкостью и за сливным отверстием,

  удельный вес.

При v >> v₀; h₀ = 0 и p₁ = p₂ имеем:

Пусть S₀  сечение сливного отверстия, тогда в идеальном случае

Q₂ = v S₀.

Реально последнее выражение записывается с некоторым коэффициентом , отражающим зависимость расхода Q₂ от неравномерности скорости v, от качества обработки отверстия, от его формы и т.д.

В результате получаем модель

Пример наглядно показывает, что даже в простой ситуации модель получается в виде нелинейного дифференциального уравнения.

16. Метод наименьших квадратов в одномерном случае

Метод наименьших квадратов известен давно и применяется весьма широко и повсеместно.

Преимущество метода  простые вычисления для определения степенной аппроксимации.

Рассмотрим простейший случай.

Рис. 16. Одномерная система

Проводим эксперимент N раз и получаем пары чисел

x_i, y_i; i = 1, 2, ..., N

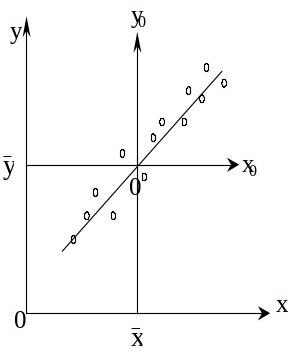
Рис. 17. Экспериментальные данные

1) Делается допущение, что y зависит от x линейно, а несоответствие линейной зависимости обуславливается случайными факторами.

Т.о. ставится произвольно задача найти линейную зависимость

с постоянными коэффициентами a₀, a₁, которые позволят для любого экспериментального значения x_i вычислить некоторую оценку , которая нас удовлетворит в каком-либо смысле.

2) Второе допущение состоит в том, что положительные и отрицательные отклонения должны компенсировать друг друга и искомая зависимость должна проходить через точку с координатами, равными средним значениям

т.е. искомое уравнение должно удовлетворять соотношению

(*)

3) Следующее допущение касается аддитивности ошибки, т.е. мы принимаем, что

(**)

Перенесем начало координат в точку и введем новые (центрированные) значения переменных

Вычитая теперь из (**) уравнение (*), получим

Обратим внимание на то, что все отмеченные выше допущения принимаются как аксиомы и направлены на то, чтобы получить ошибку как линейную функцию неизвестных коэффициентов аппроксимирующей зависимости

_i = f(a₁).

4) Наконец, самое основное допущение касается критерия оптимизации, который принимается в виде

Принятие критерия в таком виде (который дает имя методу) позволяет однозначно и легко вычислить искомый коэффициент известным методом поиска экстремума функции одной переменной:

Далее из (*) находится а₀: