
10546
.pdf
1 y′ = v′lnu + v 1 u′
yu
и отсюда
y′ = uv (v′lnu + v 1 u′) = uv lnuv′ + vuv−1u′. u
Этот прием, называемый логарифмическим дифференцированием, применим также для упрощения нахождения производных. Например,
|
(x +1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y = |
|
x −1 |
, |
|
ln y = 2ln(x +1)+ |
1 |
ln(x −1)− 3ln(x + 4)− x, |
|||||||||||||||||
(x + 4)3 ex |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
1 |
y′ |
2 |
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
= |
|
|
|
+ |
|
|
− |
|
|
−1, |
|
|
|
||||||||
|
|
y |
x +1 |
2(x −1) |
x + 4 |
|
|
|
||||||||||||||||
|
(x +1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y′ = |
|
|
x −1 |
|
2 |
+ |
|
1 |
|
− |
|
|
3 |
−1 |
||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
(x +1) |
|
2(x −1) |
|
|
||||||||||||||
|
(x + 4)3 ex |
|
|
|
|
|
|
|
x |
+ 4 |
|
|||||||||||||
19.5. Сводка формул производных и правил дифференцирования.
Сведём в одном месте формулы производных элементарных функций
(x |
α |
)′ = αx |
α−1 |
, |
1 |
′ |
||
|
|
|
|
|
|
|||
|
|
|
||||||
|
|
|
|
|
x |
|
||
|
|
(sin x)′ = cos x, |
||||||
|
|
(tgx)′ = |
|
1 |
|
|
, |
|
|
|
cos2 x |
||||||
|
|
|
|
|
||||
= − |
1 |
|
( |
|
|
)′ = |
1 |
|
|
|
, |
|
x |
|
|||||||
2 |
|
|
|
|
||||||
2 x |
|
|||||||||
|
x |
|
|
|
|
|
||||
(cos x)′ |
= −sin x |
|
||||||||
(ctgx)′ = − |
|
1 |
|
|
|
|
||||
|
sin2 x |
|
||||||||
|
|
|
|
|
|
|||||
(arcsin x )′ = |
1 |
|
|
|
|
, |
|
|
|
(arccos x)′ = − |
1 |
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1− x2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
1 − |
x |
2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(arctgx)′ = |
|
1 |
|
|
|
|
, (arcctgx)′ = − |
|
|
1 |
, |
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
+ x2 |
|
|
|||||||||||||||||
|
1 |
|
|
|
1+ x |
|
|
|||||||||||||
(loga x)′ = |
1 |
|
|
|
1 |
, |
(ln x)′ = |
1 |
|
, |
|
|
|
|
||||||
lna |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|||||
141

(a x )′ = a x ln a, |
(ex )′ = ex , |
а также формулы, выражающие правила дифференцирования:
(u ± v)′ = u′ ± v′,
|
|
′ |
|
′ |
|
′ |
|
u |
= |
u v − v u |
|||||
|
|
|
|
|
|
, |
|
|
v |
2 |
|
||||
v |
|
|
|
|
|||
′ |
′ |
|
′ |
′ |
′ |
c = const, |
||
(u v) |
= u v |
+ v u , |
(c f ) |
= cf , |
||||
|
' |
|
|
x = x(t) |
|
y′ |
||
[ f (u(x))]x |
= fu′u′x , |
|
|
y′x = |
t |
. |
||
|
|
|||||||
|
|
|
|
y = y(t) |
|
xt′ |
||
19.6. Производные высших порядков. Выше речь шла о понятии производной или первой производной функции. Производные высших порядков определяются по индукции.
Производной n-го порядка называется производная от (n −1) -ой производной. Так, вторая производная функции y = f (x) равна
f ′′(x) = ( f ′(x))′ .
Отметим физический смысл второй производной в случае, когда задан закон изменения пути как функция времени, т.е. s = s(t). Тогда s′(t) есть скорость, а s′′(t) – ускорение в момент времени t .
Если функция задана явно, то вычисление ее высших производных сводится к повторному дифференцированию. Если функция y задана не-
явно F (x, y) = 0 , то для отыскания её n-ой производной нужно соответст-
вующее число раз продифференцировать определяющее ее уравнение, помня, что y и все её производные есть функции независимой переменной x . Например,
x2 + y2 =1 2x + 2yy′ = 0 y′ = − x .
|
|
y |
||
Дифференцируя второй раз, получим |
|
|
|
|
2 + 2y′ y′ + 2y y′′ = 0 y′′ = − |
1+ y′2 |
= − |
x2 + y2 |
. |
|
|
|||
|
y |
|
y3 |
|
x = x(t)
В случае параметрического задания функции ,α ≤ t ≤ β
y = y(t)
142
первая производная равна y′ |
= |
y′(t) |
.Для нахождения второй производной |
|
|||
x |
|
x′(t) |
|
продифференцируем это равенство по x , имея ввиду, что t есть функция x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
' |
|
|
|
|
′ |
(t) |
' |
|
|
|
1 |
|
|
|
ɺɺɺ |
ɺɺ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
yx − xy |
|
||||||
|
|
|
|
|
|
y"xx |
= (y′x )t |
tx' = |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
, |
|||||||||||
|
|
|
|
|
|
|
′ |
(t) |
|
|
′ |
|
|
ɺ3 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
t |
|
|
x (t) |
|
|
|
|
x |
|
|||||
где точка сверху обозначает производную поt . |
|
|
|
|
|
|
||||||||||||||||||||||||||||
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x = acost |
|
|
|
|
|
yx' |
= |
|
bcost |
= − |
b |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgt , |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
−asint |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
y |
= bsint |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
'' |
|
b |
' |
|
1 |
|
|
|
|
b |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
||||
yxx |
= − |
|
ctgt |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
. |
|
|
|||
|
|
ɺ |
asin |
2 |
|
|
|
|
|
|
a |
2 |
sin |
3 |
t |
|
|
|||||||||||||||||
|
|
a |
t |
|
|
x |
|
|
t |
−asint |
|
|
|
|
|
|
|
|||||||||||||||||
Аналогично можно найти производные более высоких порядков.
143
Лекция 20. Вектор-функция
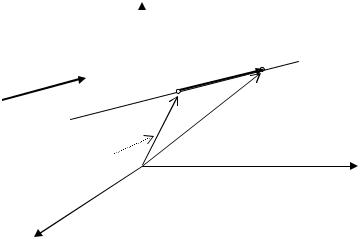
20.1. Вектор-функция и её задание. К понятию вектор-функции
или векторной функции скалярного аргумента мы приходим, изучая переменный вектор. С переменным вектором мы уже имели дело, когда записывали уравнение прямой в пространстве в векторной форме (см. рис. 20.1)
|
z |
|
s = { m,n, p} |
|
t s M |
|
M |
|
s |
0 |
|
r(t) = { x(t), y(t), z(t)}
r0
y
x |
|
|
|
|
Рис. 20.1 |
|
|
r(t) = r0 + t s = (x0 |
+ tm)i + (y0 |
|
− ∞ < t < +∞ . |
+ tn) j + (z0 + t p)k, |
|||
|
|
|
|
Суть в том, что координаты радиус-вектора r(t) есть некоторые функции переменного t . Поэтому естественно следующее определение векторфункции: если каждому значению вещественного переменного t из некоторого промежутка по определённому закону поставлен в соответствие вектор
|
|
|
|
r(t) = x(t)i + y(t) j + z(t)k, |
|
то будем говорить, что в промежутке |
α ≤ t ≤ β задана вектор-функция |
r(t) . |
|
Вектор r(t) будем считать выходящим из начала координат, т.е. это |
|
радиус-вектор. При этом конец вектора |
M(x(t), y(t),z(t)) будет описывать |
некоторую линию L(годограф), параметрические уравнения которой да- |
|
ются формулами |
|
x = x(t), |
|
|
α ≤ t ≤ β |
y = y(t), |
|
z = z(t),
144
Таким образом, задание вектор-функции эквивалентно заданию трёх скалярных функций, являющихся координатами её радиус-вектора. Название
– годограф происходит от греческих слов hodos – путь и grapho – пишу. Началом всех векторов для построения годографа может служить любая фиксированная точка плоскости.
20.2. Предел, непрерывность и производная вектор-функции. Понятия предела, непрерывности и производной вектор-функции введём «покоординатно»,а именно: вектор-функция
r(t) = x(t)i + y(t) j + z(t)k
в некоторой точке t0 имеет предел, непрерывна, дифференцируема, если соответственно имеют предел, непрерывны и дифференцируемы в этой точке функции x(t), y(t), z(t). При этом полагают
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ lim x(t) k |
|||
limr(t) = lim x(t) i |
+ lim y(t) j |
||||||||||
t→t0 |
|
t→t0 |
t→t0 |
|
|
t→t0 |
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
d r |
= d x i + d y j + d z k . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
dt |
dt |
|
|
||
Производной вектор-функции |
r(t) в точке t0 называется предел |
||||||||||
отношения приращения |
r к приращению |
t , когда последнее стремит- |
|||||||||
ся к нулю. В математической символике это определение записывается известным образом:
r′(t0 ) = lim |
r |
= lim |
r(t0 + |
t) − r(t0 ) |
= |
dr |
. |
t |
|
t |
|
||||
t→0 |
t→0 |
|
dt |
||||
Геометрический смысл производной векторной функции скалярного аргумента близок к геометрическому смыслу производной числовой функции. Будем предполагать, что годограф вектор-функции в точке
M0 (x0 , y0 , z0 ) = M0 (x(t0 ), y(t0 ), z(t0 ))
имеет касательную, определяемую как предельное положение секущей M0M . Направление движения точки соответствующее возрастанию параметра t обозначим на рисунке стрелкой (см. рис. 20.2). Рассмотрим два случая, когда значение аргумента t0 получает как положительное, так и от-
рицательное приращение t . Вектор r = r(t0 + t) − r(t0 )– |
это хорда |
(греч.χορδη – струна). В случае положительного приращения |
t > 0он на- |
145 |
|
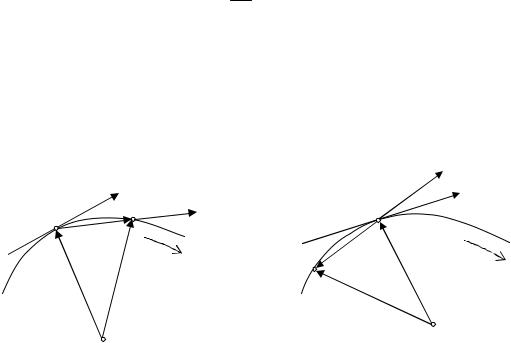
правлен по секущей в сторону, соответствующую возрастанию аргумента
t0 , а в случае t < 0 |
r |
в противоположном направлении. Вектор же |
|
|
t |
будучи коллинеарным вектору r в любом случае будет направлен вдоль секущей в сторону, соответствующую возрастанию параметраt .Поскольку секущая при t → 0примет положение касательной к годографу, то вектор
dr = lim r dt t→0 t
будет касательным вектором к годографу в данной точке. Итак, производная вектор-функции в данной точке – это вектор касательный к её годографу и направленный в сторону возрастания параметра.
|
|
|
|
∆ |
|
∆ |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∆ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
∆ |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
∆ |
(t |
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
∆ |
(t ∆t) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ 0 |
||
∆ 0 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 20.2
Пример. Годограф вектор-функции
r(t) = (t − sint) i + (1− cost) j
это циклоида, т.е. траектория фиксированной точки окружности единичного радиуса, катящейся по оси Ox без скольжения. Пусть t – время и окружность делает полный оборот за 2π секунд. Тогда вектор-функция
r(t) = (t − sint) i + (1− cost) j
задаёт не только траекторию движения точки, но и закон движения.
На рис.20.3 в точках траектории через каждые 2π/10 сек. построены векторы скорости точки
146
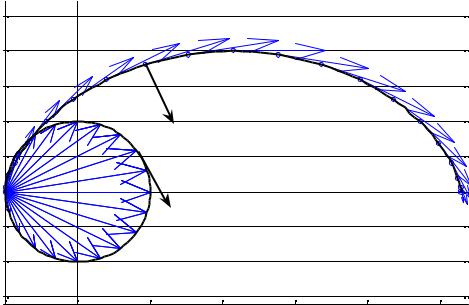
|
|
r′(t) = |
|
|
|
|
|
|
(1− cost) i |
+ sint j . |
|
|
|
Самая большая скорость точки будет в момент времени |
t = π. Построен |
|||||
также годограф скорости точки. В одной из точек построен вектор ускоре- |
||||||
ния. Это вектор касательный к годографу скорости в соответствующей |
||||||
точке. |
|
|
|
|
|
|
2.5 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1.5 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
-0.5 |
|
|
|
|
|
|
-1 |
|
|
|
|
|
|
-1.5 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Рис.20.3
20.3. Уравнения касательной и нормальной плоскости к пространственной кривой. Пусть криваяLзадана параметрическими уравнениями
x = x(t), |
|
|
α ≤ t ≤ β |
y = y(t), |
|
|
|
z = z(t), |
|
и имеет в рассматриваемой точкеM0 (x0 , y0 , z0 ) = M0 (x(t0 ), y(t0 ), z(t0 )) касательную. Это значит, что у вектор-функции
r(t) = x(t)i + y(t) j + z(t)k
существует производная в этой точке
|
dr |
= { x′(t0 ), y′(t0 ),z′(t0 )}. |
||
r′(t0 ) = |
|
|
||
|
||||
|
dt |
0 |
|
|
|
|
|
|
147 |
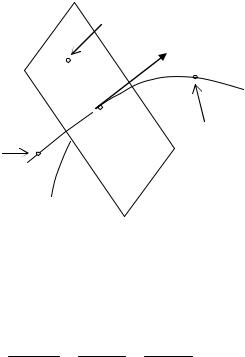
Нормальной плоскостью к данной кривой L в точке |
M0 называют |
|
плоскость, проходящую через точку M0 перпендикулярно |
касательной к |
|
кривой в этой точке (см. рис. 20.4). |
|
|
Пусть |
K(X,Y,Z) – произвольная точка касательной к кривой L в |
|
точке M0 , |
а N(u,v,w) – точка нормальной плоскости к кривой в этой же |
|
точке. |
|
|
N(u,v,w)
r′(t0 )
 M0
M0
K(X,Y,Z)
M(x, y, z)
Рис.20.4
У нас есть все данные, чтобы написать уравнения касательной, например в
канонической форме
X − x0 = Y − x0 = Z − x0 . x′(t0 ) y′(t0 ) z′(t0 )
Соответственно, уравнение нормальной плоскости будет иметь вид
x′(t0 )(u − x0 ) + y′(t0 )(v − x0 ) + z′(t0 )(w − x0 ) = 0
Пример. Написать уравнения касательной к кривой
x
y
z
= cost, |
|
|
|
( 0,1, π) |
= sint, 0 ≤ t ≤ π |
в точке |
M |
0 |
|
= t /2, |
|
|
4 |
|
|
|
|
Точке M0 соответствует значение параметра |
t0 = π/ 2. Для вектор- |
функции |
|
r(t) = cost i + sint j + t k |
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
148 |
|
|
|

|
|
|
|
|
|
|
|
|
1 |
|
|
вычисляем касательный вектор |
r′(t) = −sint i |
+ cost j |
+ |
k, |
|||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
r′(t0 ) = r′(π/ 2) = { −1, 0, 0.5} |
|
|
|
|
|||||||
Записываем уравнения касательной в канонической форме |
|
|
|
||||||||
|
x − 0 |
= |
y −1 |
= |
z − π/4 |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|||
|
0 |
0.5 |
|
|
|
|
|
||||
|
|
|
|
y =1, |
|
|
|
|
|
||
или в виде пересечения двух плоскостей |
|
. |
|
|
|
||||||
|
|
|
|
2x + z − π = |
0 |
|
|
|
|||
Уравнение нормальной плоскости
−1(x − 0) + 0(y −1) + 0.5(z − π/4) = 0
или 8x − 4z + π = 0 (см.рис. 20.5)
Рис. 20.5
149

Лекция 21. Дифференциал
21.1. Дифференциал. Прежде, чем ввести понятие дифференциала, рассмотрим следующую задачу: пусть скорость велосипедиста в данный момент
v =12 |
км |
= |
10 |
м |
|
. |
|
сек |
|||||
0 |
час |
3 |
|
|
||
|
|
|
|
|
|
|
Какое расстояние он проедет за следующие 30 секунд? Ответ, очевидно, не однозначный:
1)если он продолжает двигаться с той же скоростью, то пройденный путь
S= v0 t =100м;
2)если он «ускорился» (или движется под гору), то расстояние
S> 100м;
3)если устал (или движется в гору), то пройденное им расстояние
S< 100м.
Самый реальный прогноз (лучше иметь какую-то информацию, чем неопределённость)
S = v0 t = S′(t0 ) t ,
причём этот прогноз тем точнее, чем меньше промежуток времени t
.Например, за время t = 3cek. велосипедист проедет расстояние S =10м,и эта величина «почти» точная, даже если велосипедист созна-
тельно начнёт менять скорость своего движения.
Теперь рассмотрим математическую задачу. Пусть задана некоторая
функция |
y = f (x), и мы умеем вычислять её значение в точке |
x0 , т.е. |
||
f (x0 ) известно, а требуется найти её значение в точке x0 + x |
при за- |
|||
данном |
x. Допустим, что процедура «прямого» вычисления значения |
|||
функции |
f ( x0 + x) |
нам недоступна. Например, нужно |
найти |
|
arctg1.02, зная значение |
arctg1= π |
≈ 0.7854. Возникает естественное же- |
||
|
|
4 |
|
|
лание: в равенстве |
|
|
|
|
|
|
150 |
|
|
