10546

Лекция 24. Кривизна. Приближённое решение уравнений

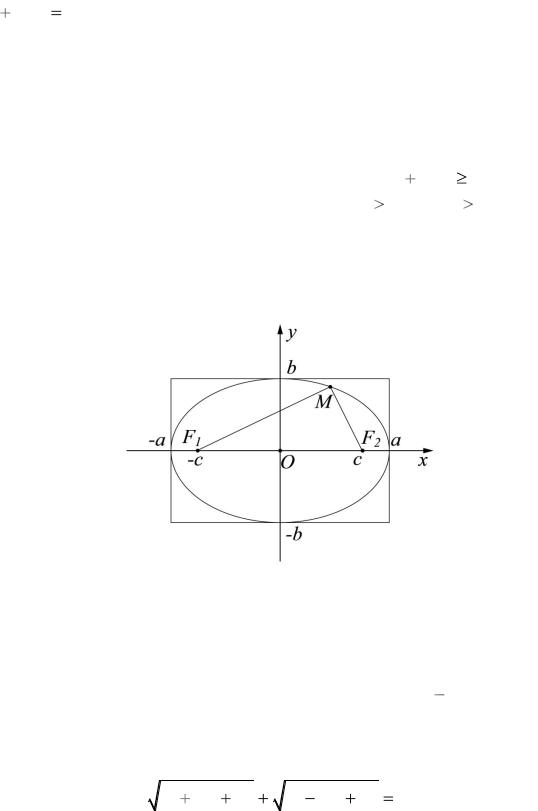
24.1.Понятие кривизны. Одна и та же кривая в разных точках искривлена по-разному. Например, синусоида в точках пересечения с осью абсцисс почти прямая, а в вершинах дуг наиболее искривлена. Более того, на различных участках она искривлена в разном направлении. Нельзя ли как-то определить кривизну в данной точке кривой? Оказывается можно. Для этого определим сначала среднюю кривизну некоторого участка кривой.

Пусть при перемещении точки по кривой из положения M1 в положение M2 касательный вектор повернётся на угол Δα. Обозначим прой-

Δα = 0. Таким образом, средняя кривизна любого участка прямой линии равна нулю, что не противоречит здравому смыслу.

Пусть теперь точка «прошла» некоторую дугу sокружности радиуса R . Поскольку длина дуги окружности с центральным углом Δα равна

s = RΔα, то средняя кривизна любой части окружности равна

171

Естественно теперь ввести понятие кривизны в данной точке как предел средней кривизны, когда длина участка s стремится к нулю

k = lim Δα = dα , s→0 s ds

т.е. кривизна равна производной угла поворота касательного вектора по длине кривой.

24.2. Вычисление кривизны плоской кривой. Для вывода формулы кривизны кривой y = f (x)продифференцируем по переменнойsравенство, выражающее геометрический смысл ее производной

α(s) = arctg y′x .

Пользуясь правилом дифференцирования сложной функции, получим

эта формула показывает, что кривая имеет положительную кривизну для выпуклых функций.

Пример. Найдем кривизну параболы y = x2

2

k = (1+ 4x2 )32 .

Из этой формулы видно, что при больших значениях x кривизна параболы близка к нулю, т.е. парабола «выпрямляется», а наибольшая кривизна будет в начале координат и равна 2.

24.3. Геометрический смысл кривизны. Назовем радиусом кривиз-

ны для кривой в заданной точке величину R = 1 . Используя формулу кри- k

визны k = 1 для окружности радиуса R , дадим следующую геометриче-

R

скую интерпретацию радиуса кривизны произвольной кривой. Пусть кривизна в данной точке равна k . Через эту точку проведем окружность той же кривизны с центром на нормали к кривой в этой точке. Радиус этой окружности R =1/ k и принимается за радиус кривизны кривой в этой точке.

На следующем рисунке приведён график функции y = cosx и соответствующая окружность. Кривизна в любой точке вычисляется по формуле

Рис. 24.3

В начале координат k(0) = −1. Кривизна отрицательна, так как кривая выпукла вверх. Радиус окружности кривизны R =1/ −1 =1. Центр окружности расположен в начале координат.

173

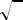
Свойство кривизны изменять своё значение вдоль кривой используется, например, при сопряжении прямолинейных участков железнодорожных путей с закруглениями. Допустим, что прямолинейный участок примыкает к участку, имеющему вид дуги окружности. Причем они в точке соединения имеют общую касательную, т. е. соединение гладкое. Но при движении поезда в этой точке мгновенно возникнет центробежная сила, создавая резкий толчок, что нежелательно. Поэтому такие участки соединяют с помощью некоторой переходной кривой. Вдоль неё кривизна постепенно нарастает от нулевого значения до величины обратной радиусу закругления. Аналогичная ситуация наблюдается при конструировании различного рода зубчатых зацеплений.

ма. Например, написав для уравнения x2 − 2 = 0 формулу для одного из его корней x1 = 2 , мы только указали математическую операцию, с помощью которой этот корень можно вычислить. Поэтому возникает необходимость приближённого вычисления корня данной функции. Обычно задают допустимую погрешность ε , с которой этот корень нужно вычислить. Это значит нужно найти такой промежуток [a,b], содержащий ко-

убеждаемся, что в промежутке [ 0,1] есть, по крайней мере, один корень нашего уравнения. Покажем, что других корней в этом промежутке нет. Производная функции f ′(x) = 3x2 +1 > 0 положительна, поэтому график функции один раз пересечёт ось Ox, переходя от отрицательного значения к положительному значению. Иногда эту процедуру «отделения» корня

Абсцисса точки их пересечения и есть искомый корень (см. рис. 24.4). В нашем случае из рисунка видно, что корень расположен в промежутке 0,6 < ξ < 0,8, т. е. мы ещё сузили промежуток, где находится корень. Далее применим так называемый метод деления отрезка. Вычисляем значение функции в средине отрезка f (0,7) = 0,343− 0,300 = 0,043 > 0 и на одном

174

из его концов, например, f (0,6) = 0,36 0,6− 0,4 = −0,184 < 0. Следовательно, корень находится в промежутке 0,6 < ξ < 0,7, т. е. корень вычислен с точностью до 0,1. Ясно, что эту процедуру уточнения значения корня можно продолжить, но она требует слишком большого количества вычислений.

Рис. 24.4

Познакомимся с методами, которые быстрее ведут к цели. Но для их применения нужна дополнительная информация о поведении функции в промежутке, на котором изолирован корень. Заметим, что вторая производная функции f ′′(x) = 6x > 0 положительна, следовательно, график функции в промежутке0,6 < x < 0,7 имеет вид (см. рис. 24.5)

B

хорда

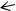f (b) = 0.043

a = 0.6

b = 0.7

f (x)

f (a) = −0.184

касательная

A

Рис. 24.5

175

Если провести хорду АВ, то точка a1 пересечения хорды с осью Ox даст очередное приближение к искомому корню слева. Приближение справа можно получить, найдя точку пересечения b1 касательной (проходящей через точку В ) с осью Ox. Запишем уравнение хорды АВ как уравнение прямой, проходящей через две точки

Отсюда при y = 0 получаем a1 ≈ 0,681. Уравнение касательной в точке В имеет вид

y − f (b) = f ′(b)(x − b)

или

y − 0,043 = 2,47(x − 0,7).

Полагая y = 0, получаем b1 ≈ 0,683. Проверим, не «потеряли ли» мы ко-

Значения функции на концах промежутка [0,681; 0,683] оказались разных знаков. Значит, мы вычислили корень с точностью ε = 0,002. Если же в качестве приближённого значения корня взять среднее арифметическое

ξ = (a1 + b1)/ 2 = 0,682, то корень будет вычислен с точностью ε = 0,001.

176

ba

f ′ < 0

f ′ > 0 f ′′ < 0 f ′′ < 0

Рис. 24.6

Эту процедуру уточнения корня методом хорд и касательных можно продолжить, однако с методом касательных нужно быть внимательнее. Построив касательную не в той точке промежутка, можно не приблизиться к корню, а удалиться от него (см. рис 24.6). На рисунке хорды проведены пунктирной линией. Анализ возможных ситуаций показывает, что касательную нужно проводить из той точки кривой y = f (x), в которой знак функции совпадает со знаком второй производной.

177