
9278
.pdf40
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна
П = mgh, |
(2.7) |
где h — высота, отсчитанная от нулевого уровня, для которого П0 = 0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h'),
П = – mgh.
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:
Fупр = – kx,
где k — коэффициент упругости (в случае пружины — жесткость), а знак минус указывает, что сила упругости направлена в сторону, противоположную деформации. По третьему закону Ньютона, для преодоления силы упругости надо приложить силу
F = – Fупр = kx.
Элементарная работа dA, совершаемая силой F при малой деформации dx, равна dA = ;F = : F,
а полная работа
x
A = kxdx = kx2 / 2 +C = П +C
0
идет на увеличение потенциальной энергии пружины.
Если принять, что потенциальная энергия недеформированного тела (при х = 0) равна нулю, то С=0. Таким образом, потенциальная энергия упругодеформированного тела
П =kx2 /2.
41
Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы — энергия механического движения и взаимодействия:
Е= Т + П.
§3. Закон сохранения энергии
Выведем закон сохранения энергии. Для этого рассмотрим замкнутую систему материальных точек массами m1, m2, …, mn, движущихся со скоростями , !, … , .
Пусть ;′ , ;′!, … , ;′ — равнодействующие внутренних консервативных сил,
действующих на каждую из этих точек, а ; , ;!, … , ; — равнодействующие внешних сил. При v<<с массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
m |
dυ1 |
|
= F ′+ F , |
|||
|
|
R |
|
R |
R |
|
|
|
|
|
|
||
1 |
|
dt |
1 |
1 |
||
m |
|
R |
|
= F ′+ F , |
||
|
dυ2 |
|
||||
|
|
|
|
|
R |
R |
2 |
|
|
2 |
2 |
||
|
dt |
|||||
. . . . . . . . |
||||||
m |
|
R |
|
|
|
|
|
dυn = F ′+ F . |
|||||
|
|
|
|
|
R |
R |
n |
|
dt |
|
n |
n |
|
Пусть все точки за какой-то интервал времени dt совершают перемещения |
||||
F , F !, … , F . Умножим каждое |
из уравнений скалярно на соответствующее |
|||
|
F R = |
F , |
R |
R |
перемещение, и, учитывая, что |
E |
E R |
|
|
|
|
получим |
||
|
R |
|
|
|
|
m1 (υ1dυ1 ) −(F1′+ F1 )dx1 = 0, |
|||||
R |
R |
R |
R |
R |
= 0, |
m2 (υ2 dυ2 ) |
−(F2′+ F2 )dx2 |
||||
. . . . . . . . . . . . |
|||||
R |
R |
R |
R |
R |
= 0. |
mn (υn dυn ) |
−(Fn′+ Fn )dxn |
||||
Сложив эти уравнения и учитывая, что система замкнута, т. е. |
|||
|
|
|
, |
; |
+ ;! |
+ + ; |
= 0 |
Получим
42
n |
R R |
n R |
R |
= 0 , |
|
|
|
miυi dυi |
− Fi 'dxiI |
|
|
|
|||
i =1 |
|
i =1 |
|
|
|
|
|
n |
|
n |
|
|
|
|
|
mi vi dvi |
= d( mi V i2 / 2 ) = dT . |
|
(3.1) |
||||
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
n |
R |
R |
= dП |
|
|
|
|
|
|
||
dT - бесконечно малое изменение кинетической энергии всей системы, а − Fi 'dxi |
|||||||
i =1
- бесконечно малая работа всех действующих в системе внутренних консервативных сил, взятая с обратным знаком, т. е., согласно (2.2), бесконечно малое изменение потенциальной энергии системы dII. Следовательно, для всей системы в целом
dT+ dП = 0,
откуда полная механическая энергия замкнутой системы
T + П = Е = const |
(3.2) |
Выражение (13.2) представляет собой закон сохранения механической энергии: в замкнутой системе тел, между которыми действуют только консервативные силы, механическая энергия сохраняется, т. е. не изменяется со временем.
Взамкнутой системе тел, силы взаимодействия между которыми консервативны, взаимные превращения механической энергии в другие виды отсутствуют. Такие системы называются замкнутыми консервативными системами. Существует еще один вид систем – диссипативные системы – такие системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации или рассеяния, энергии. Строго говоря, все системы в природе являются. диссипативными. При движении тела в замкнутой консервативной системе происходит непрерывное превращение кинетической его энергии в потенциальную и обратно в эквивалентных количествах, так что полная энергия остается неизменной. Закон сохранения и превращения энергии - фундаментальный закон природы, он справедлив как для систем микроскопических тел, так и для систем микротел.
Взамкнутой системе, в которой действуют силы трения, полная механическая энергия системы при движении убывает. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении»
43 |
|
|
механической энергии всегда возникает эквивалентное |
количество |
энергии |
другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой.
§ 4. Удар абсолютно упругих и неупругих тел
Примером применения законов сохранения количества движения и энергии при решении реальной физической задачи является удар абсолютно упругих и неупругих тел.
Удар (или соударение) – это встреча двух или более тел, при которой взаимодействие длится очень короткое время. Исходя из данного определения, кроме явлений, которые можно отнести к ударам в прямом смысле этого слова (столкновения атомов или биллиардных шаров), сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и т. д. При ударе в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.
Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.
Абсолютно упругий удар — столкновение двух тел, в результате которого в обоиx взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.
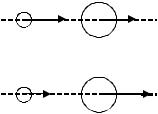
Для абсолютно упругого удара выполняются закон сохранения количества движения и закон сохранения кинетической энергии. Обозначим скорости шаров массами m1 и m2 до удара через υ 1 и υ 2, после удара — через υ '1 и υ '2 (рис. 15). Так
|
|
|
|
44 |
|
|
|
|
|
|
|
|
|
|
|
|||||
как удар |
центральный, то |
|
будем |
рассматривать модули величин. Законы |
||||||||||||||||
сохранения имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m1 |
m2 |
|
m1v1 |
+ m2 v2 = m1υ1′ + m2υ2′ , |
(4.1) |
|||||||||||||||
|
|
|
|
|||||||||||||||||
V1 |
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m1 |
m2 |
|
|
m1v12 |
|
|
m2 v22 |
|
m1υ1′2 |
|
m2υ2′2 |
|
|
|||||||
|
|
|
|
|
|
+ |
= |
+ |
. |
(4.2) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
V`1 |
V`2 |
2 |
|
|
2 |
2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Произведя соответствующие преобразования в выражениях (4.1) и (4.2), |
||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 (υ1′ + v1 ) = m2 (υ2′ + v2 ) , |
|
|
|
|
|
(4.3) |
|||||||||||||
|
m1 ( v12 +υ1′2 ) = m2 ( v22 +υ2′2 ) , |
|
|
|
|
|
(4.4) |
|||||||||||||
откуда |
υ1′ + v1 |
|
= υ2′ + v2 . |
|
|
|
|
|
|
|
|
|
|
|||||||
Решая совместно уравнения (4.3), (4.4) и (4.5), находим |
|
|||||||||||||||||||
|
υ′ = |
( m1 − m2 )v1 + 2m2v2 |
, |
|
|
|
|
|
(4.6) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
|
m1 + m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
υ2′ = |
( m2 − m1 )v2 + 2m1v1 |
. |
|
|
|
|
|
(4.7) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
m1 + m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для анализа полученных результатов разберем несколько примеров: |
|
|||||||||||||||||||
1) при v2 =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ1′ = |
m1 − m2 |
v1 , |
|
|
|
|
|
|
|
|
|
(4.8) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
m1 + m2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
υ2′ = |
|
2m1 |
|
v1 . |
|
|
|
|
|
(4.9) |
|||||||
|
|
|
|
m1 + m2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
45 |
|
|
|
Проанализируем выражения (4.8) и (4.9) для различных |
|
|
|
|
|
|
|
масс: |
|
|
|
а) m1=m2. Если второй шар до удара висел |
|
|
V`2 |
неподвижно (v2=0) (рис.16), то после удара остановится |
|
|
|
первый шар (υ'1 = 0), а второй будет двигаться с той же |
V1 |
V2 V`2 |
скоростью и в том же направлении, в котором двигался |
|
|
|
|
|
|
Рис. 16 |
первый шар до удара (υ`2 = v1); |
|
|
|
|
б) m1>m2. Первый шар продолжает двигаться в том |
же направлении, как и до удара, но с меньшей скоростью (υ'1 < υ1). Скорость второго шара после удара больше, чем скорость первого после удара (υ'2>υ'1) (рис. 17);
m1 |
m2 |
в) m1<m2. Направление движения первого шара |
||
V1 |
v2=0 |
при ударе изменяется – |
шар отскакивает обратно. |
|
|
|
|
|
|
m1 |
|
Второй шар движется в ту же сторону, |
в которую |
|
m2 |
|
|
|
|
|
двигался первый шар |
до удара, но |
с меньшей |
|
|
|
|||
V`1 |
V`2 |
скоростью (рис. 18); |
|
|
|
|
|
|
|
Рис. 17
m1 m2
V1 v2=0
m2
m1
V`1 |
V`2 |
|
Рис. 18
m1 m2
V1 V2
г) m1>> m2 (например, столкновение со стеной). Из уравнений (4.8) и (4.9) следует, что
υ'1 = - v1, υ'2 ≈ 2m1v1/m2 ≈ 0.
2) при m1=m2. Выражения (4.6) и (4.7) будут иметь вид υ'1 = v2, υ'2 = v1,
т. е. шары равной массы обмениваются скоростями.
m1+m2
V
Рис. 19
Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. Продемонстрировать абсолютно неупругий удар
|
46 |
|
|
|
можно с помощью шаров из пластилина (глины), движущихся |
навстречу друг |
|||
другу (рис. 19). |
|
|
|
|
Если массы тел m1 и m2, их скорости до удара υ 1 и υ 2, то используя закон |
||||
сохранения импульса, можно записать |
|
|||
|
m1υR1 + m2υR2 = (m1 + m2 )υR , |
|
||
откуда |
υR = |
m1υR1 + m2υR2 |
. |
(4.10) |
|
||||
|
|
m1 + m2 |
|
|
Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим количеством
движения. В частном случае, если массы шаров равны (m1 = m2), то
= ( + !)/2.
Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от величины самих деформаций, а от скоростей деформаций, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит потеря кинетической энергии, перешедшей в тепловую или другие формы энергии, Эту потерю можно определить по разности кинетической энергии тел до и после удара:
m v 2 |
m |
v2 |
|
|
( m + m |
2 |
)v 2 |
|||
T = |
1 1 |
+ |
2 |
2 |
|
− |
1 |
|
. |
|
|
|
|
|
|
|
|||||
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Используя (4.10), получим
T = |
|
m1m2 |
|
( v − v |
|
)2 . |
||||||
|
2( m1 + m2 ) |
2 |
||||||||||
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|||||
Если ударяемое тело было первоначально неподвижно (v2 = 0), то |
||||||||||||
|
|
v = |
|
m1v2 |
|
|
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
m1 + m2 |
|
|
||||||
|
T = |
|
m2 |
|
m1v12 |
. |
|
|||||
|
m1 |
+ m2 |
2 |
|
||||||||
|
|
|
|
|
|
|||||||
Когда m2>>m1, (масса неподвижного тела очень большая), то v<<v1, и почти вся кинетическая энергия дела при ударе переходит в другие формы энергии. Абсолютно
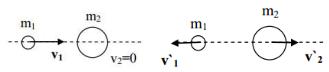
47 |
|
|
неупругий удар — пример того, как происходит |
потеря |
механической |
энергии под действием диссипативных сил. |
|
|
Примеры решения задач
Задача 1. Шар массой m1, движущийся горизонтально с некоторой скоростью υ, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю своей кинетической энергии первый шар передал
второму? |
|
|
Дано: |
|
Решение: |
|
||
m1, m2, υ |
|
Сделаем рисунок: а) система шаров до удара, б) система |
|
|
шаров после удара. |
|
|
|
ε = ? |
|
|
|
|
|
а) б)
Доля энергии, переданной первым шаром второму, выразится соотношением кинетических энергий второго шара после удара и первого шара до удара:
ε = |
T |
= |
m υ2 |
= |
|
m |
|
υ' |
2 |
|
(1) |
2 |
2 2 |
|
2 |
|
2 |
|
|
||||
T |
'2 |
|
m |
υ |
|
||||||
|
|
m υ |
|
|
|
|
|
|
|||
|
1 |
|
1 1 |
|
1 |
1 |
!J |
|
|||
где Т1 — кинетическая энергия |
первого |
шара |
до удара; |
и T2 – скорость и |
|||||||
кинетическая энергия второго шара после удара.
Как видно из формулы (1), для определения а надо найти !J . Согласно условию задачи, импульс системы двух шаров относительно горизонтального направления не изменяется и механическая энергия шаров в другие виды не переходит. Пользуясь этим, запишем закон сохранения импульса и механической энергии:
m1υ1 = m1υ '1 + m2υ '2 , |
(2) |
||||||
m υ2 |
m υ '2 |
m υ '2 |
|
||||
1 1 |
= |
1 1 |
+ |
2 2 |
. |
(3) |
|
2 |
2 |
2 |
|||||
|
|
|
|
||||
Решим совместно уравнения (2) и (3):
48
υ= 2m υ2
'1 1
2 m1 + m2
Подставив это выражение в формулу (1) и сократив на υ1 и m1, получим
ε = |
m |
|
2m υ2 |
|
2 |
4m m |
|
|
2 |
|
1 1 |
|
= |
1 2 |
|
. |
|
m |
υ (m + m ) |
(m + m ) |
2 |
|||||
|
|
|
|
|
|
|||
|
1 |
1 1 2 |
|
1 2 |
|
|
Из найденного соотношения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров.
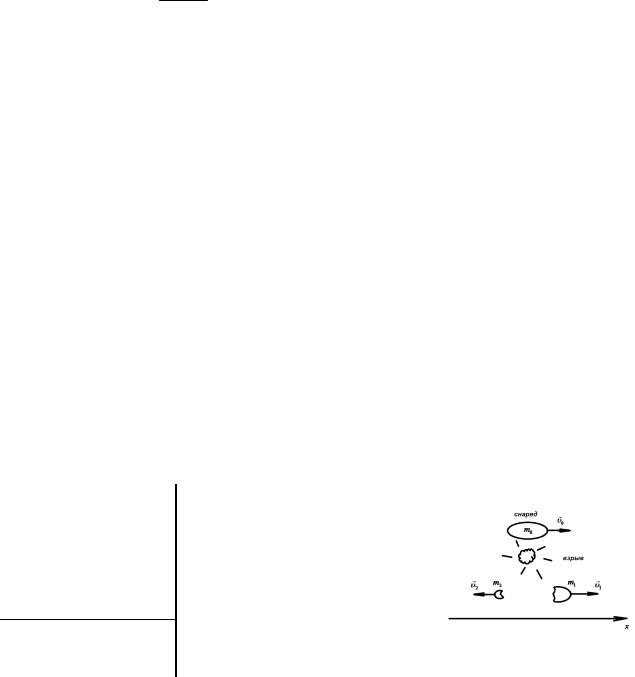
Задача 2. Снаряд, летящий горизонтально со скоростью 72 км/ч, разорвался на два неравных осколка. Больший осколок, масса которого составляла 0,8 массы всего снаряда, продолжал двигаться в прежнем направлении, но с увеличенной скоростью 108 км/ч. Найти скорость меньшего осколка. Считать, что меньший осколок движется в горизонтальном направлении противоположно движению большего осколка.
Дано:
υ0 =72 км/ч= 20 м/c
υ1 =108 км/ч= 30 м/с
m1 =0,8m0
υ2 = ?
Решение:
Сделаем рисунок. Внутренние силы, возникающие при взрыве снаряда, намного превышают действие любых внешних сил.
Следовательно, для данной задачи можно считать систему замкнутой и применять закон сохранения импульса в векторной форме
|
|
R |
R |
R |
|
|
p0 |
= p1 |
+ p2 , |
|
R |
R |
R |
|
где |
p0 - импульс снаряда до взрыва, |
p1 |
и p2 - импульсы осколков. |
|
Спроецируем закон сохранения импульса на ось x : |
||||
|
|
p0 = p1 |
− p2 , |
|
или |
|
|
|
|

49
m0υ0 =m1υ1 −m2υ2 .
Учтем, что по условию задачи масса первого осколка составляет 0,8 массы всего снаряда.
m1 =0,8m0 , значит m2 =0,2m0 .
Тогда закон сохранения импульса может быть записан в виде:
m0υ0 =0,8m0υ1 −0,2m0υ2 ,
υ0 =0,8υ1 −0,2υ2 .
Отсюда искомая скорость второго осколка:
υ2 = 0,8υ1 −υ0 ,
0, 2
υ2 =20 м/с.
Ответ: υ2 =20 м/с.
Задачи для самостоятельного решения
1.Под действием постоянной силы вагонетка проходит путь 100 м и приобретает скорость 12 м/с. Определить работу этой силы, если масса вагонетки 200 кг и коэффициент трения качения 0,05.
2.Артиллерийское орудие массой 900 кг выстреливает ракетой массой 15 кг с начальной скоростью 320 м/с относительно Земли под углом 60˚ к горизонту. Какова скорость отката пушки?
3.Шар массой 5 кг движется навстречу второму шару массой 3,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом составляли 2 м/с и 4 м/с соответственно. Определите, какое время будут двигаться эти тела после удара, если коэффициент трения 0,2.
4.Какую мощность развивает спортсмен при прыжке в высоту, если его масса 71,4 кг и за время 0,5 с центр его тяжести поднимается на 2 м?
5.Грузовик поднимается вверх по пологому склону со скоростью 5 м/с и спускается по той же дороге со скоростью 7 м/с. Какую скорость будет иметь грузовик на
