9278

10

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется тремя скалярными уравнениями:

Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы. Если материальная точка движется в пространстве, то, как уже было сказано, она обладает тремя степенями свободы (координаты х, у и z), если по некоторой поверхности, то двумя степенями свободы, если по кривой, то одной степенью свободы.

Исключая t в уравнениях (1.1) и (1.2), получим уравнение траектории движения материальной точки. Траектория движения материальной точки — линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Рассмотрим движение материальной точки вдоль произвольной траектории (рис. 2). Отсчет времени начнем с момента, когда точка находилась в положении А. Длина участка траектории АВ, пройденного материальной точкой с момента начала

перемещением.

Естественно, что при прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения | | равен пройденному пути s.

11

§ 2. Скорость

Для характеристики движения материальной точки вводится векторная величина – скорость, которая определяет как быстроту движения, так и его направление в данный момент времени. Пусть материальная точка движется по

Мгновенная скорость есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости υ направлен по касательной к

мгновенной скорости с течением времени изменяется, пользуются скалярной величиной <υ> – средней скоростью неравномерного движения на данном участке:

υ = s .

Из рис. 3 вытекает, что < > > | < >t |, так как s > | | и только в случае

прямолинейного движения

∆ = |∆|.

Если выражение ds = υdt (см. формулу (2.2)) проинтегрировать по времени в

t

В случае равномерного движения, когда числовое значение мгновенной скорости постоянно, выражение (2.3) примет вид

t +Δt

s =υ dt =υ t .

t

Путь, пройденный точкой за промежуток времени от t1 до t2, дается интегралом

t2

s = υ(t) dt .

t1

§3. Ускорение и его составляющие

Вслучае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физической величиной, характеризующей быстроту изменения скорости по модулю и направлению, является ускорение.

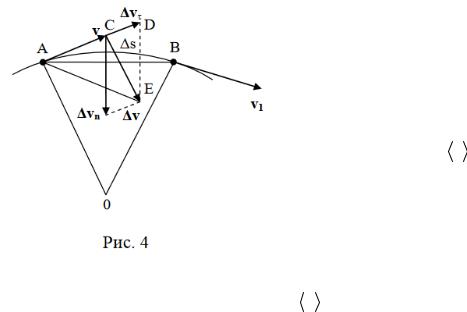
Пусть вектор V задает скорость точки А в момент времени t. За время t движущаяся точка перешла в положение В и приобрела скорость, отличную от V как по модулю,

так и направлению, равную = + . Перенесем вектор в точку А и найдем

(рис. 4).

определяет быстроту изменения скорости в данный момент времени t и является

тангенциальной составляющей ускорения aτ:

некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует υn/АВ = υ1/r, но так как АВ = υ t, то

υn =υυ1 . t к

В пределе при t → 0, → .

перпендикулярный скорости, будет направлен к центру круга ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также

центростремительным ускорением).

ускорения движение можно классифицировать следующим образом:

1)аτ = 0, аn = 0 — прямолинейное равномерное движение;

2)аτ = а = const, an = 0 — прямолинейное равнопеременное движение. При таком виде движения

aτ = a = υ = υ2 −υ1 . t t2 −t1

Если начальный момент времени t1 = 0, а начальная скорость υ1 = υ0, то, обозначив t2 = t и υ2 = υ, получим a = (υ – υ0)/t, откуда

υ = υ0 + at.

15

Проинтегрировав эту формулу в пределах от нуля до произвольного момента времени t, получим формулу для пройденного пути в случае равнопеременного движения:

tt

s = υ dt = (υ0 + at)dt = υ0 t + at 2 / 2 ;

00

3)аτ = f(t), аn = 0 — прямолинейное движение с переменным ускорением;

4)аτ = 0, аn= const. При аτ = 0 скорость по модулю не изменяется, а изменяется по направлению. Из формулы аn= υ2/r следует, что радиус кривизны должен быть постоянным. Следовательно, имеем дело с равномерным движением по окружности;

5)аτ =0, аn = f(t) — равномерное криволинейное движение;

6)аτ =const, аn ≠ 0 — криволинейное равнопеременное движение;

7)аτ = f(t), аn ≠ 0 — криволинейное движение с переменным ускорением.

§4. Угловая скорость и угловое ускорение

В случае движения материальной точки по окружности по аналогии с линейными скоростью и ускорением вводятся угловая скорость и угловое

ускорение.

s

Пусть точка движется по окружности радиуса R (рис. 6). Ее положение через малый промежуток времени зададим углом . Угловой скоростью называется векторная

величина, равная первой производной угла поворота тела по времени:

Направление вектора угловой скорости задается правилом винта: вектор угловой скорости совпадает по направлению с поступательным движением острия винта, головка которого вращается в направлении движения точки по окружности (рис. 7). Размерность угловой скорости [ω] =Т -1, а ее единица — радиан в секунду

(рад/с).

17

Нормальная составляющая ускорения

Таким образом, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость υ, тангенциальное ускорение aτ нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость

ω, угловое ускорение β) выражается следующими формулами:

s = Rφ, υ = Rω, aτ = Rβ, an = ω2R.

В случае равнопеременного движения точки по окружности (β = const)

Задача 1. Уравнение движения материальной точки вдоль оси имеет вид: = ++ , где А=2 м, В=1 м/с, С=- 0,5 м/с3. Найти координату х, скорость υx и ускорение аx точки в момент времени t=2с.

Для нахождения тангенциальной составляющей ускорения, вычислим угловое ускорение:

ε (t )= dω =8 рад/с2, dt

Ответ: а=57,8 м/с2.

Задачи для самостоятельного решения

1.Велосипедист проехал первую половину времени своего движения со скоростью

18км/ч, а вторую половину времени – со скоростью 24 км/ч. Вычислить среднюю скорость велосипедиста.

2.Трамвай отошел от остановки с ускорением 0,2 м/с2. Достигнув скорости 36 км/ч, он в течение 2 мин двигался равномерно, а затем, затормозив, равнозамедленно прошел до следующей остановки путь 100 м. Определить среднюю путевую скорость трамвая на участке между остановками.

3.Тело, пущенное по наклонной плоскости вверх от ее основания со скоростью 1,5 м/с, возвратилось в туже точку со скоростью 1 м/с, двигаясь вверх и вниз с постоянными ускорениями. Найти среднюю скорость за все время движения.

4.Поезд, двигаясь равнозамедленно, в течение 60 с уменьшает свою скорость от 40 км/ч до 28 км/ч. Найти ускорение поезда и расстояние S, пройденное им за время торможения.