1. невырожденные с «+»;

2. Невырожденные с «·»;

3. с фиксированным определителем относительно «+»;

4. диагональные с «+»;

5. Диагональные с «·»;

6. Диагональные с ненулевыми элементами, «∙».

8. Подгруппы. Разложения группы по подгруппам

 Пусть задана группа G. Говорят, что H – подгруппа группы G ( ), если выполняются условия:

1. ;

2. 

Примеры.

1. H = {1} – подгруппа (сама группа есть подгруппой).

2. – множество подстановок на множестве М.

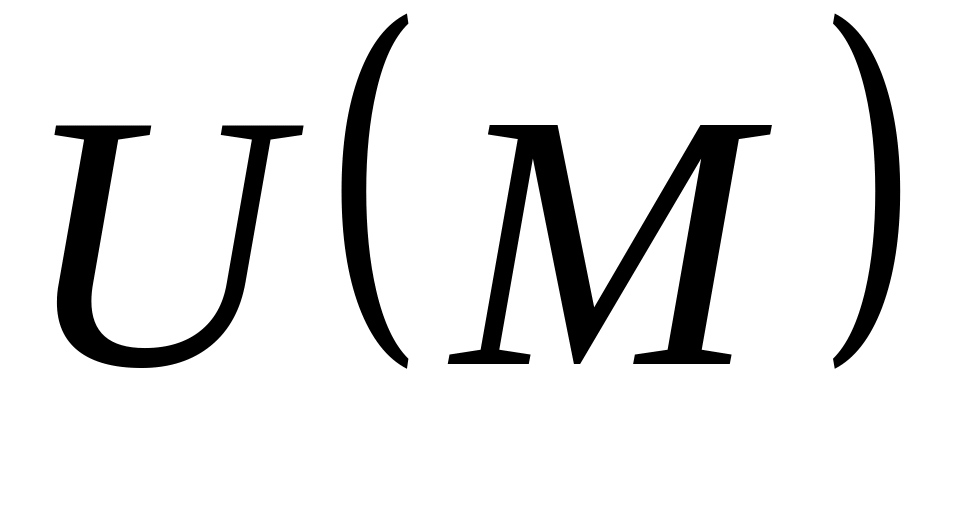3. – множество четных подстановок.

 Пусть задана группа G и H – подгруппа G. Говорят, что , если или для некоторого h.

Данное отношение является отношением эквивалентности:

1. x = 1·x, 1  H. 

2. y = hx, h  H x = h^-1·x, h^-1  H  2. 

3.  3.

Таким образом получаем разбиение группы G на классы эквивалентности, которые назыв. правыми классами смежности, а разбиение назыв. правым разложением.

Утверждение 2.4 Если g – некоторый представитель правого класса смежности, то все его элементы записываются в виде h∙g, h  H. Обозначение: Hg.

Докажем от обратного: пусть существует y – из класса смежности Hg такое, что y  hg, h  H, но – противоречие, то есть все элементы класса можно записать в виде hg  Hg 

Если группа конечна, то классов смежности – конечное число:

Возьмем и построим отображение след. образом: .

Утверждение 2.5 Отображение _g – биекция.



1. Докажем инъективность. От обратного: – противоречие, то есть _g – инъекция.

2. Докажем сюръективность. От обратного: 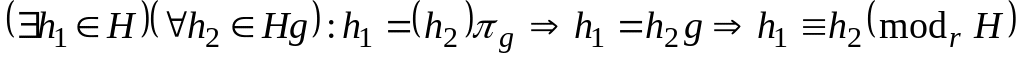, т.е. h₁  Hg – противоречие. Значит_g – сюръекция.

3. Из 1. и 2. следует, что _g – биекция.



ТЕОРЕМА 2.2 (Лагранжа) Порядок подгруппы конечной группы является делителем порядка группы.

Пусть , тогда , где k – число правых классов смежности.

 Число классов смежности назыв. индексом подгруппы и обозначается G:H. Его можно определить, разделив порядок группы на порядок подгруппы и тогда теорема Лагранжа может быть записана след. образом: .

 Правым сдвигом группы G назыв. Gg.

Утверждение 2.6 Если и – два произвольных правых класса смежности, то существует некоторый правый сдвиг группы G, отображающий на .

 Говорят, что , если или для некоторого .

 Классы g_iH назыв. левыми классами смежности.

Примеры.

1. Пусть , ; , .

G:H = 2, т.е. , где g – нечетная подстановка. .

2. Пусть , а .

G:H = 3  |G| = 6 |H|=2

Тогда , .

 Если N – подгруппа G такая, что правые и левые разложения по этой подгруппе совпадают, то N назыв. нормальным делителем группы G и обозначается .

9. Циклическая подгруппа

Возьмем любой элемент группы G и рассмотрим множество . Это множество будет образовывать подгруппы G, порожденные элементом g.

Для конечной группы всегда существует такое m  Z, что различными будут только , а . Такое m назыв. порядком элемента: Or(g). Для циклических подгрупп |(g)| = Or(g).

Утверждение 2.7 Порядок элемента циклической подгруппы является делителем порядка группы.

 Группа назыв. простейшей, если у нее нет нетривиальных подгрупп.

10. Фактор-группа

Введем след. операцию над классами: , где – класс смежности, содержащий элемент .

Утверждение 2.8 Если , и – нормальный делитель группы, то .

 

Утверждение 2.9 Если из и следует, что , причем то же самое выполняется и для левого разложения, то .

 Таким образом, при введенной операции классы смежности образуют группу, которая назыв. фактор-группой и обозначается .

11. Гомоморфизм и эпиморфизм

 Отображение назыв. гомоморфизмом группы G₁ в группу G₂, если .

 Гомоморфизм обладает точно таким же свойством, как и изоморфизм, но функция гомоморфизма не обязательно биективна.

 Отображение на группу (сюръективное отображение) назыв. эпиморфизмом.

Примеры.