Раздел іі Группы

1. Общие понятия и определения

 Если на некотором множестве можно ввести операцию, которая сопоставляет двум элементам один элемент этого же множества, то такое множество назыв. группоидом.

 Если введенная операция ассоциативна, то множество назыв. полугруппой.

 Если существует нейтральный элемент, то множество назыв. полугруппой с единицей.

 Группой назыв. множество M, удовлетворяющее след. условиям:

1. Введена операция 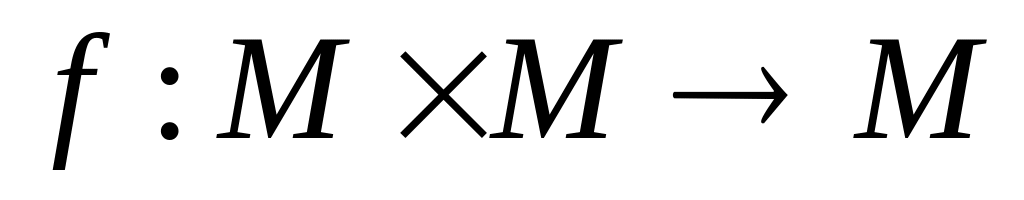, , которую назовем произведением;

2. Операция ассоциативна: ;

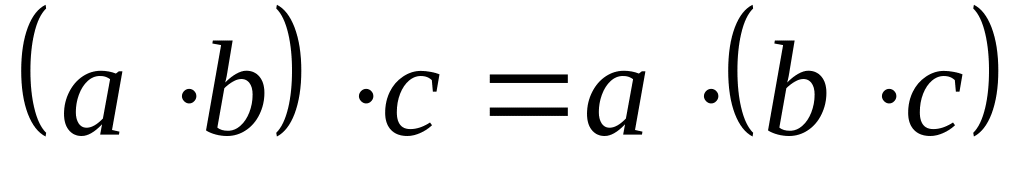3. Существует нейтральный элемент : ;

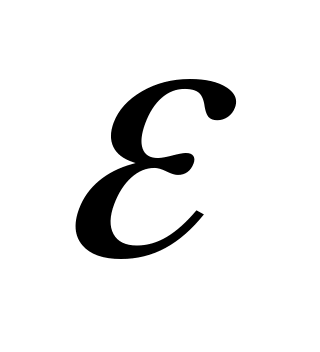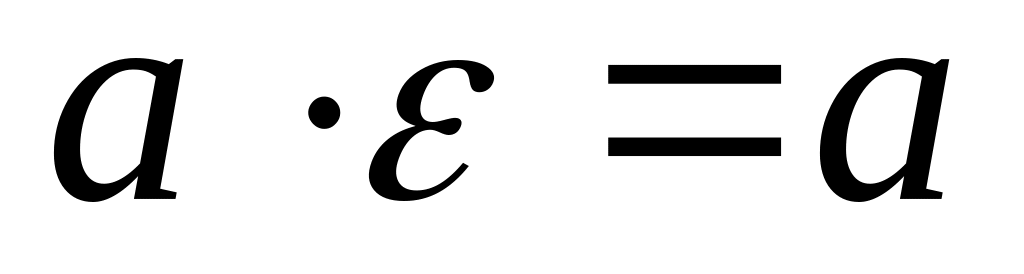4. Существует обратный элемент: .

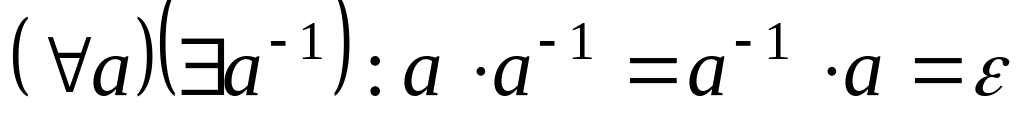 Иногда для сокращения записи точку · будем опускать.

2. Свойства групп

Утверждение 2.1 (Закон сокращения)

Следствия

1. Единственность нейтрального элемента;

2. Единственность обратного элемента.

Из ассоциативности следует, что можно определить произведение любого числа элементов .

Утверждение 2.2 .

 Число элементов группы назыв. порядком группы: .

Пусть М конечно и , тогда порядок группы перестановок будет равен m!.

 Если , то группа назыв. коммутативной или абелевой.

 Если в некоммутативной группе для некоторых элементов a, b выполняется , то эти элементы назыв. перестановочными.

Задачи. Указать, какие из указанных совокупностей отображений множества M в себя образуют группу относительно умножения:

1. множество всех отображений;

2. множество всех инъективных отображений;

3. множество всех сюръективных отображений;

4. множество всех четных подстановок;

5. множество всех нечетных подстановок;

6. множество транспозиций;

7. ;

8. 

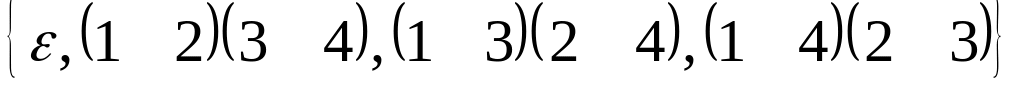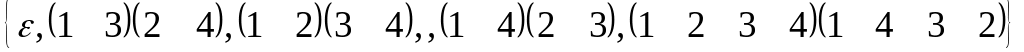
3. Циклическая группа подстановок

 Множество подстановок, являющихся степенями некоторой фиксированной подстановки , назыв. циклической группой подстановок и обозначается ().

Пример. . Определим подстановку . Полный цикл: .

, , ; .

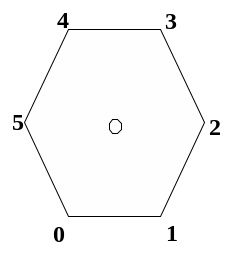Вращая на один и тот же угол, получаем цикл. Порядок подстановки равен НОК длин циклов (см. формулу утв. 1.5).

4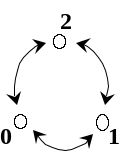 . Группа диэдра

– циклическая группа:

Плюс три симметрии:

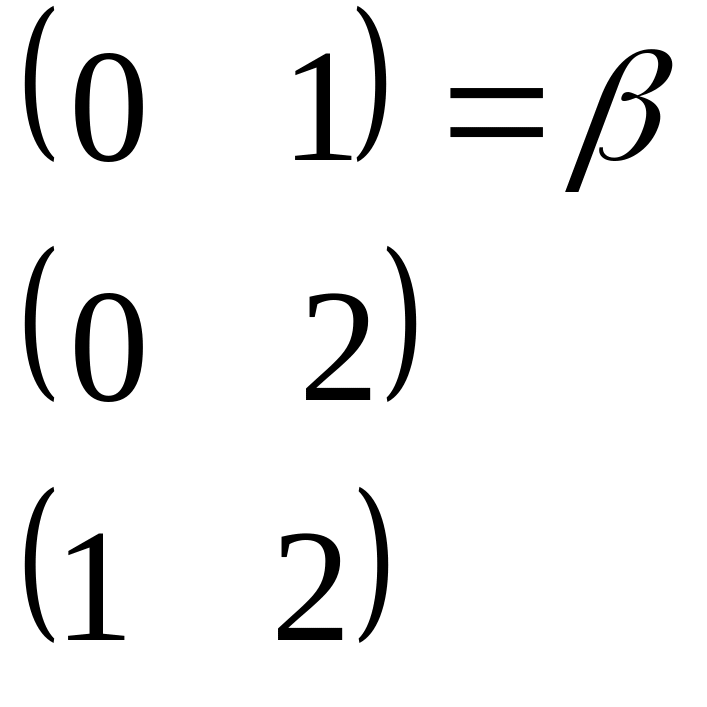
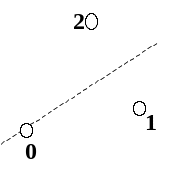
Перемножаем транспозиции:

.

Получим {, } – система образующих группу.

5. Понятие изоморфизма

1. Пусть G₁ – циклическая группа, порожденная подстановкой  = (1, 2, 3, 4, 5);

2. G₂ – множество классов вычетов по модулю 5 с операцией сложения;

3. G₃ – группа вращений пятиугольника;

4. G₄ – множество корней 5^ой степени из единицы.

 Пусть группы G₁ и G₂ заданы на множествах одинаковой мощности. Если существует биекция , обладающая свойством , то говорят, что группа G₁ изоморфна группе G₂:

 Операции ∙ и ● следует различать, т.к. они определены в разных группах.

Пример.

,

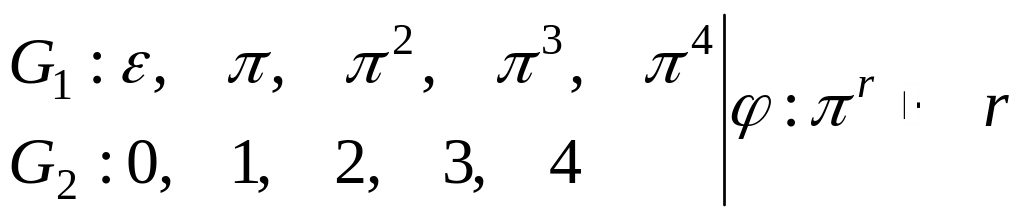то есть G₁ изоморфно G₂.

Утверждение 2.3 Если – изоморфизм, то:

1. ;

2. .

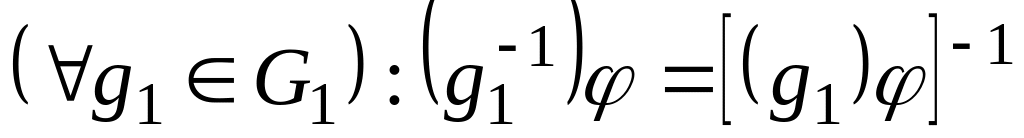1) ;

2) .

ТЕОРЕМА 2.1 (Келли) Любая группа подстановок изоморфна группе подстановок на некотором множестве.

6. Неизоморфные группы

Существуют неизоморфные группы. Пусть Q(+) – множество рациональных чисел с операцией сложения, Q⁺(·) – множество положительных рациональных чисел с операцией умножения; aQ⁺(·) – рациональное число, не являющееся квадратом; :Q(+)Q⁺(∙) – любая биективная функция. Тогда Q – противоречие. То есть данные две группы неизоморфны.

7. Антиизоморфизм

 Группы G₁ и G₂ антиизоморфны, если , где – биекция.

 Связь между подстановками и матрицами:

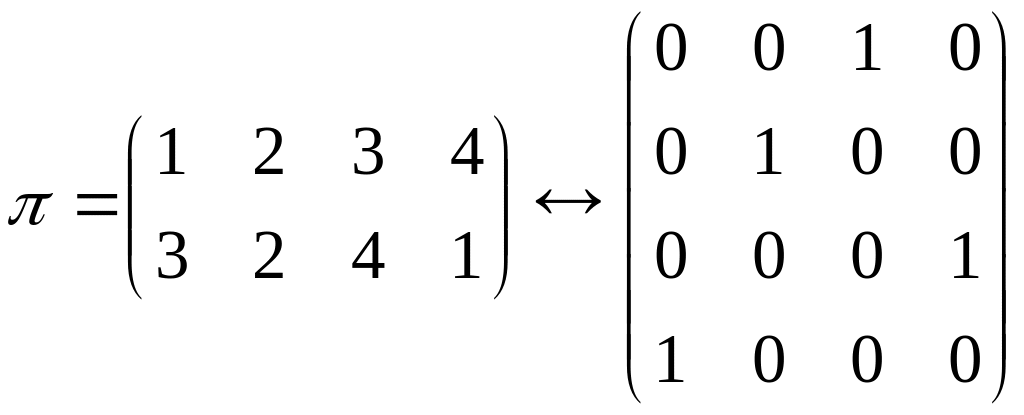– подстановочная матрица.

Задачи. Какие из указанных ниже множеств вещественных матриц фиксированного порядка образуют группу: