Тема 3. Алгоритми розв'язання проблем, сформульованих у термінах графів

У даній темі будуть розглянуті алгоритми розв’язання важливих класів проблем, сформульованих у термінах графів. При цьому ми будемо розглядати алгоритми ефективні в деякому сенсі. Традиційно критерієм ефективності виступає мінімальний час розв’язання проблеми за допомогою даного алгоритму. Тому розробка алгоритмів буде супровод­жува­тися оцінкою часу їхньої роботи. Для того щоб оцінки часу роботи алгоритму зробити уні­вер­сальними, природним буде використовувати деяку абстрактну обчислювальну машину, здатну виконувати базовий набір операцій, у яких може бути описаний будь-який алгоритм. Саме кількість операцій такої машини, що реалізує алгоритм і складе основу універсальної оцінки алгоритму.

Лекція 3.1. Базові поняття оцінки алгоритмів і їх застосування для обходу вершин графу

У цій лекції розглянемо необхідні для оцінки трудомісткості алгоритмів означення і продемонструємо їх для важливого класу алгоритмів пошуку в глибину.

1. Аналіз і оцінка алгоритмів. Будемо думати, що наша універсальна машина здатна виконувати зазначену множину операцій.

2. Алгоритм пошуку в глибину і його оцінка. Нехай G - неорієнтований зв'язний граф. У процесі пошуку в глибину вершинам графа G привласнюються номери (ПГ-номери), а його ребра позначаються. На початку ребра не позначені, вершини не мають ПГ-номерів. Починаємо з довільної вершини v₀ . Приписуємо їй ПГ-номер ПГ(v₀) = 1 і обираємо довільне ребро v₀w. Ребро v₀w позначається як «пряме», а вершина w одержує (з v₀) ПГ-номер ПГ(w) = 2. Після цього переходимо у вершину w. Нехай у результаті виконання декількох кроків цього процесу прийшли у вершину х, і нехай k — останній привласнений ПГ-номер. Далі діємо в залежності від ситуації в такий спосіб:

1. Маємо непозначене ребро ху. Якщо у вершини у уже є ПГ-номер, то ребро ху позначаємо як «зворотнє» і продовжуємо пошук непозначеного ребра, інцидентного вершині х. Якщо ж вершина в ПГ-номера не має, то нехай ПГ(y)=k+1, ребро ху помічаємо як «пряме» і переходимо у вершину в. Вершина у вважається тією, що має свій ПГ-номер з вершини х. На наступному кроці будемо переглядати ребра, інцидентні вершині в.

2. Усі ребра, інцидентні вершині х, позначені. У цьому випадку повертаємося у вершину, з якої х одержала свій ПГ-номер.

Процес закінчиться, коли всі ребра будуть позначені і відбудеться повернення у вершину v₀.

Описаний процес можна реалізувати так, щоб час роботи відповідного алгоритму складав 0(|EG|+|G|).

Такий алгоритм (алгоритм A₁) ми зараз розглянемо. Нехай граф G заданий списками суміжності, тобто N_v — список вершин, інцидентних вершині v, і v₀ — вихідна вершина, з яким починається пошук. У процесі роботи алгоритму кожна вершина графу лише один раз включається в список Q і виключається з нього. Вершина включається в цей список відразу після одержання ПГ-номера, і виключається, як тільки відбудеться повернення з цієї вершини. Включення і виключення вершин починається завжди з кінця списку, тобто Q — стек. Результат роботи алгоритму — чотири списки ПГ, F, Т і В:

ПГ(v) - ПГ-номер вершини v; F(v) - ім'я вершини, з якої вершина v одержала свій ПГ-номер; Т і В — відповідно списки орієнтованих «прямих» і «зворотніх» ребер графа G. Ці ребра одержують орієнтацію в процесі роботи алгоритму A₁. Саме, якщо ребро ху позначається з вершини х як «пряме», то в Т заноситься дуга (x, y), а як «зворотнє», то ця дуга заноситься у В.

Алгоритм A₁ пошуку в глибину в неорієнтованому зв'язному графі.

1. ПГ(v₀):=1, Q(1):=v₀, F(v₀):=0, Т:=Ø,У:=Ø, k:=1, р:=1 [k - останній приписаний ПГ-номер, р — покажчик кінця стека Q, тобто Q(p) - ім'я останньої вершини стека Q].

2. v := Q(p) [v — досліджувана вершина].

3. Переглядаючи список N_v знайти таку вершину w, що ребро vw не позначене, і перейти до п. 4. Якщо таких вершин немає, то перейти до п. 5.

4. Якщо вершина w має ПГ-номер, то позначити ребро vw як «зворотнє» і занести дугу (v,w) у список В. Перейти до п. 3 і продовжити перегляд списку N_v. Інакше k:=k+1, ПГ(w):=k, F(w):=v, ребро vw позначити як «пряме» і дугу (v, w) занести в список Т, р:=р+1, Q(p) := w [вершина w одержала ПГ-помер і занесена в стек Q]. Перейти до п. 2.

5. р:=р—1 [вершина v викреслена з Q ] Якщо р = 0, то кінець. Інакше перейти до п. 2.

Коректність алгоритму безперечна. Оцінимо його трудомісткість. Кожне включення і виключення вершини зі стека Q виконується за час 0(1). Тому для всієї роботи, зв'язаної зі зміною стека Q, достатньо часу 0(/G/). Кожне виконання п. 4 вимагає 0(1) часу, і для кожної вершини v Є VG цей пункт виконується deg v раз. Тому витрати на його виконання в цілому складуть ПРО( ∑ deg v) == 0(|EG|). Сумарний час

Виконання п.3 також складе 0(|EG|), якщо подбати про те, щоб кожна вершина списку Nv розглядалася тільки один раз при всіх виконаннях цього пункту. Цього легко домогтися, якщо, наприклад, увести таку нову функцію (масив) t, що t(v)-номер першої непереглянутої вершини в списку Nv. Тоді наступний перегляд п.3 варто починати з вершини z =Nv(t(v)).

Отже, трудомісткість алгоритму A₁ складає 0(|EG|+|G|). Зрозуміло, що цей час є найкращим з можливих з множини, тому що кожна вершина і кожне ребро графа G повинні бути переглянуті хоча б один раз.

Легко бачити, що необхідний для реалізації алгоритму A₁ обсяг пам'яті також складає 0(|EG| + |G|).

На мал. 7 ліворуч зображені граф G і списки суміжності, якими він заданий. Праворуч представлені результати застосування до цього графа пошуку в глибину з вершини v_o=1.

1

1

2

2

N1 = (3,2,5)

N2=(4,1,5)

N3=(1,5)

N4=(2,5)

N5=(2,1,3,4,7,6)

N6=(5,7)

N7=(5,6)

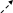
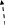
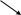
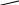
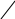
3

4

2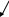

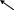
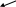
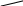
6

5

5

7

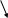
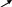
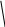
7

3

6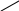

Мал. 73.1

«Прямі» ребра проведені суцільними лініями, а «зворотні» пунктирними. Кожній вершині приписаний її ПГ-номер.

Зі способу побудови безлічей Т и В безпосередньо випливають наступні твердження.

Твердження 73.1. Дуги безлічі Т утворять орієнтоване остовное дерево з коренем у вершині v_o.

Це остовне дерево часто називають остовне глибинне дерево (ОГД). Позначати його будемо також через Т.

Твердження 73.2. Якщо орієнтоване ребро (х, у) належить У, то ПГ(x)> ПГ(y), тобто «зворотні» ребра завжди ведуть до раніше пройдених вершин.

Пошук у глибину використовують як складену частину в багатьох алгоритмах. Відзначимо одну задачу, розв’язок якої можна одержати за допомогою алгоритму A₁ відразу, майже без додаткових обчислювальних витрат. Це — задача виділення зв'язних компонентів графа. Щоб вирішити її за час 0(|EG| + |G|), достатньо один раз переглянути список вершин графа, виконуючи наступні дії. Якщо вершина, що переглядається, vl має Пг-номер, то перейти до наступного. Інакше — покласти v_o=v_l, ПГ(v_o)= k+1, де k — останній привласнений ПГ-номер, і застосувати пошук у глибину. Після його закінчення (тобто виділення компонента, що містить v_l) продовжити перегляд списку, перейти до вершини v_l+1. Розрізняти вершини різних компонентів можна, наприклад, по їхній Пг-номерам, якщо для кожного компонента запам'ятати останній Пг-номер.