§ 3.4. Методы вычисления собственных значений и собственных векторов матриц
3.4.1. Основные определения.
Пусть дана квадратная матрица n-го порядка
.
(3.4.1)
Собственным вектором матрицы называется ненулевой вектор
,
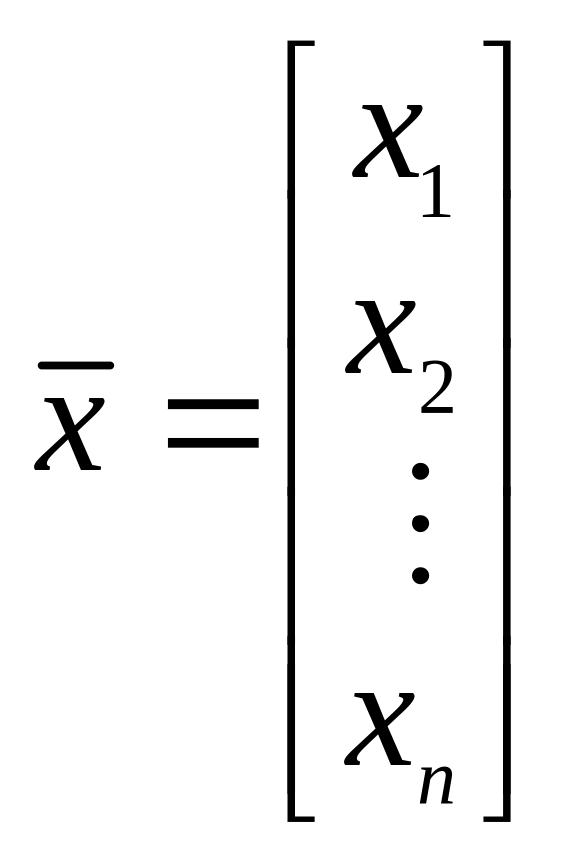(3.4.2)
удовлетворяющий системе уравнений
,
(3.4.3)
при некотором , называемом собственным числом (собственным значением).
Пример 3.4.1.
Для матрицы
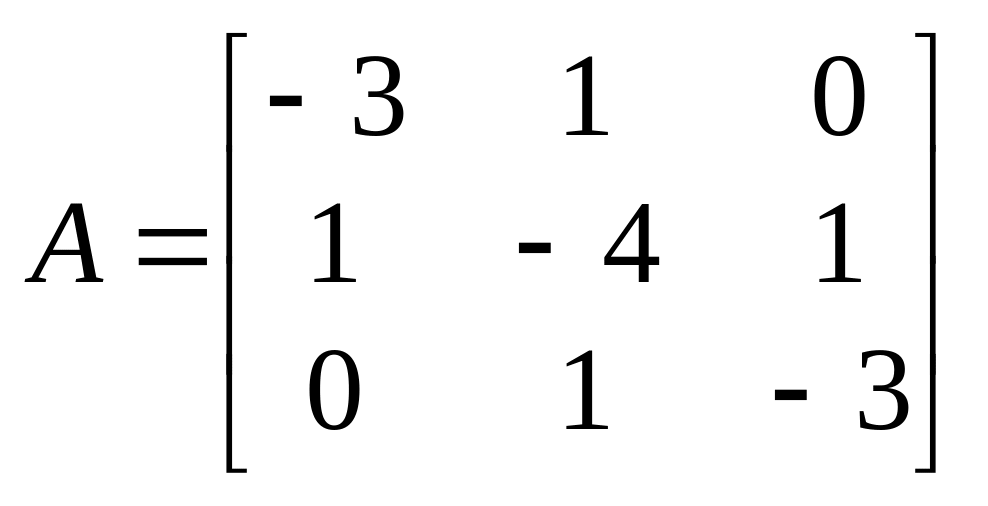вектор
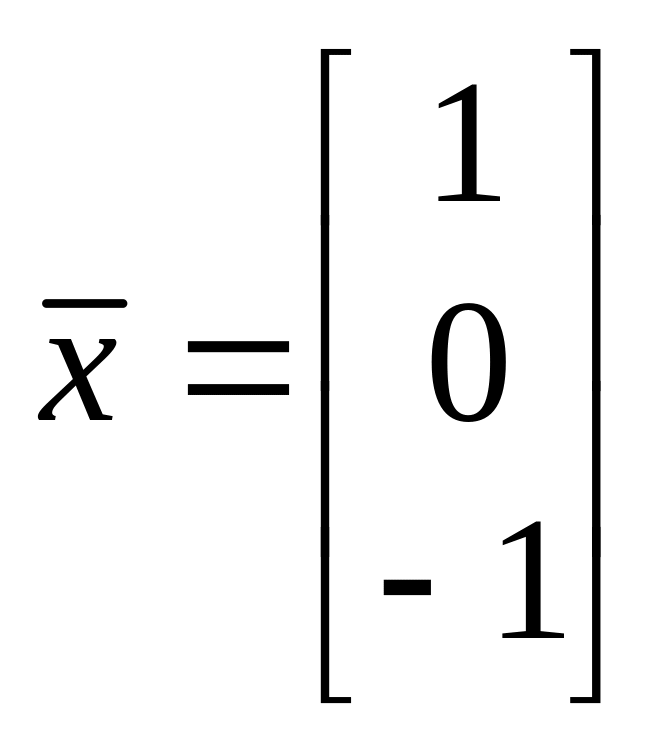– собственный, соответствующее
собственное значение
.
Проверка:
■.
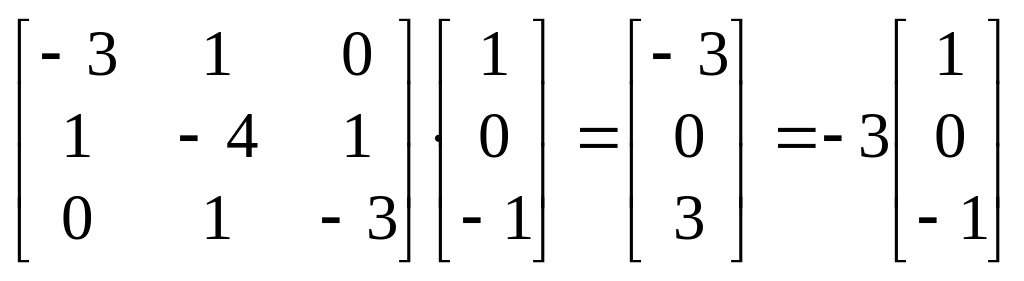3.4.2. Характеристическое уравнение.
Из определения следует, что для нахождения собственного вектора необходимо решить систему
,
(3.4.4)
подобрав предварительно число .
Для существования ненулевого решения
системы (3.4.4) необходимо и достаточно,
чтобы система была вырожденной. В этом
случае определитель матрицы
равен нулю:
,
(3.4.5)
или
.
(3.4.6)
Раскрывая определитель,
получим уравнение степени
относительно
:
.
(3.4.7)
Уравнение (3.4.7) называется характеристическим уравнением. Левая часть уравнения называется характеристическим многочленом матрицы . По основной теореме алгебры он имеет корней (с учетом кратностей).
Пример 3.4.2. Пусть требуется, используя характеристическое уравнение, определить собственные числа матрицы
.
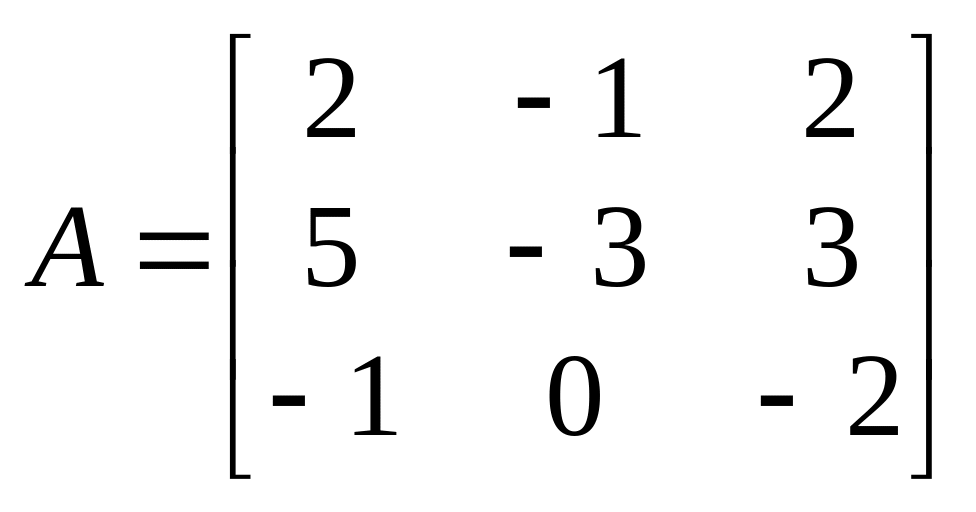Запишем характеристическое уравнение:
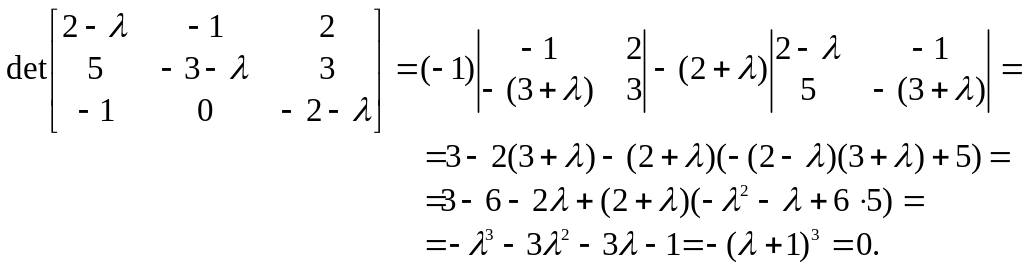
Решения характеристического уравнения:
.
Можно проверить, что вектор
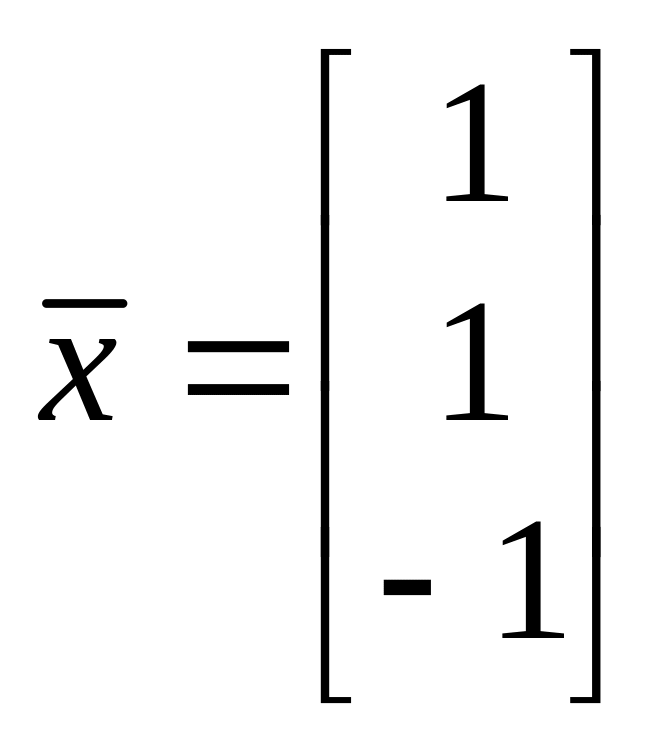
является собственным вектором.
Более того, можно показать, что никаких других собственных векторов, кроме указанного, у этой матрицы нет ■.
Пример 3.4.3. Пусть требуется, используя характеристическое уравнение, определить собственные числа матрицы
.
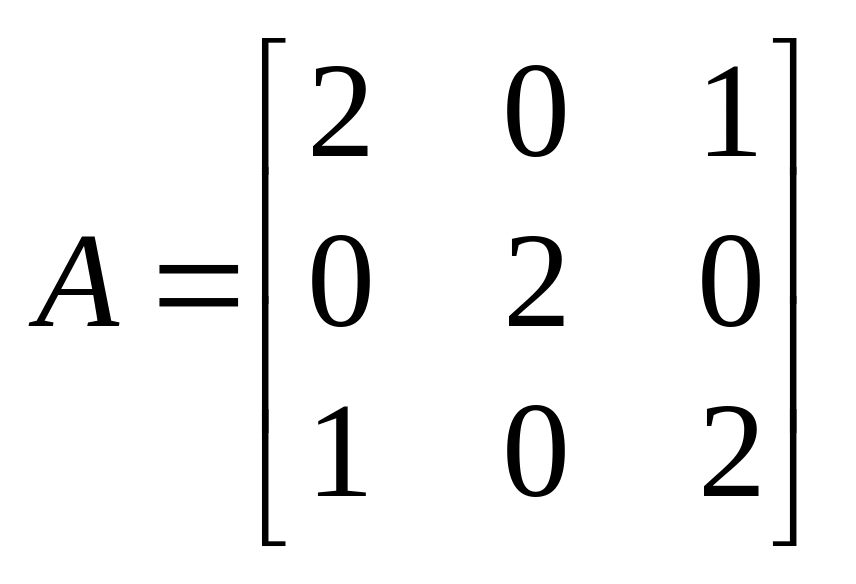Запишем характеристическое уравнение:
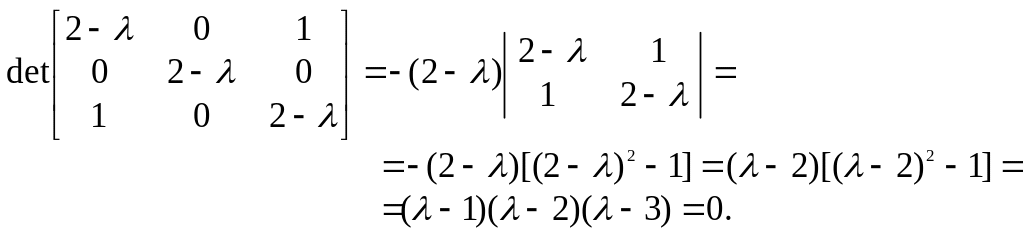
Решения характеристического уравнения:
;
;
.
Можно проверить, что соответственно вектора
;
;
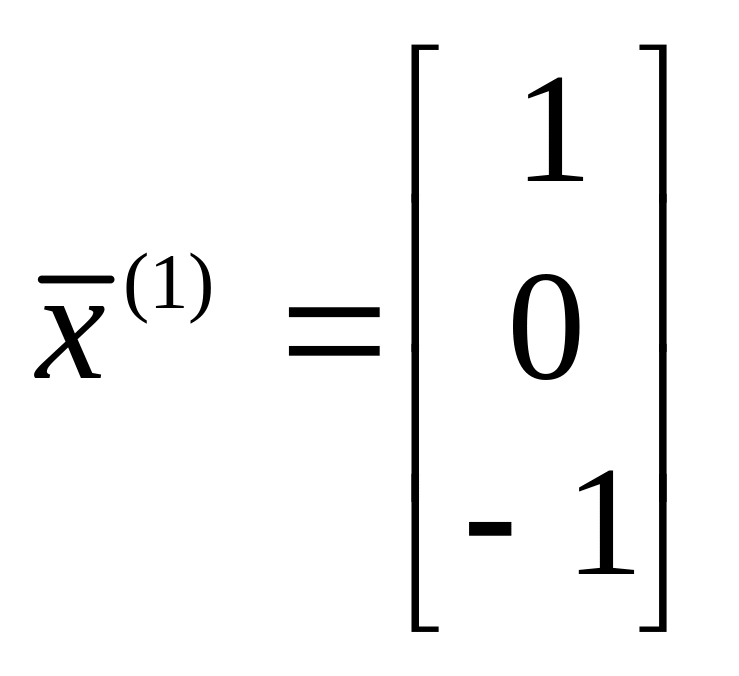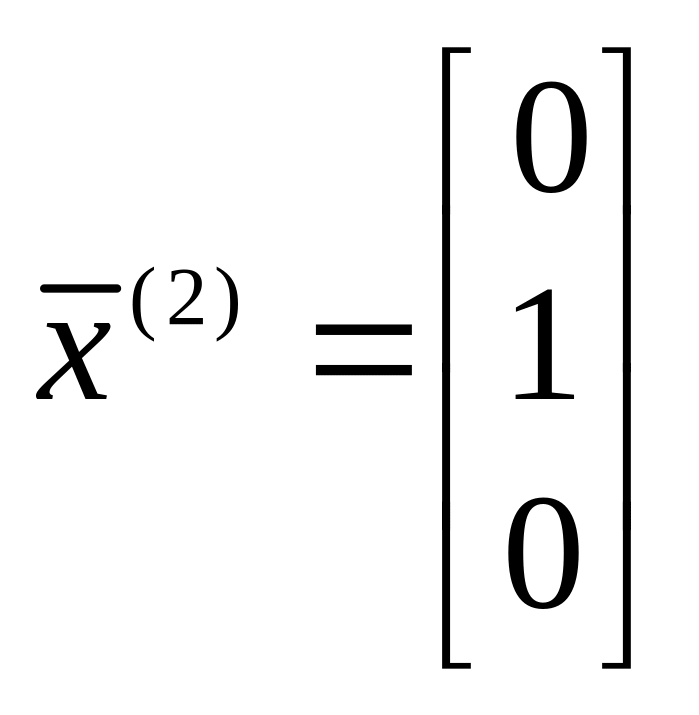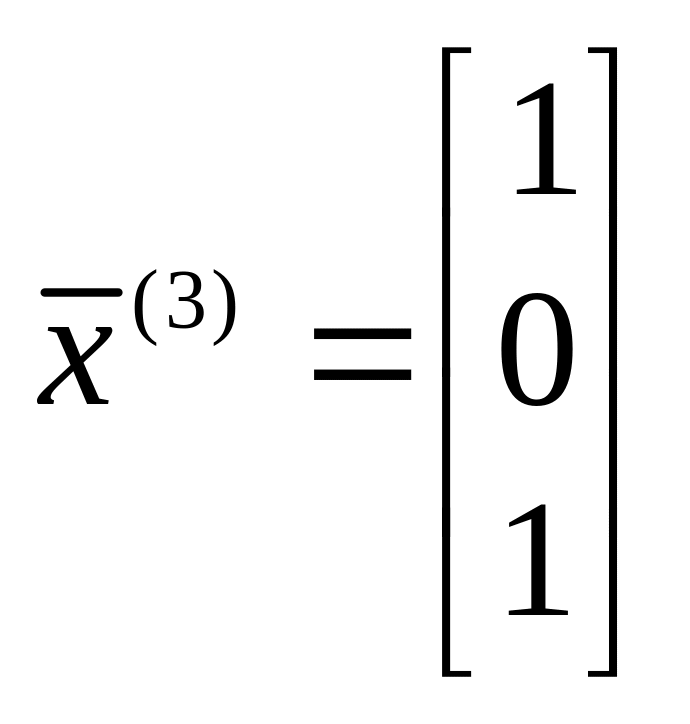
являются собственными по отношению к указанным собственным числам ■.
Как видно, в частности, из приведенных примеров число собственных векторов матрицы порядка n не всегда превосходит n (меньше n (пример 3.4.2) или равно n (пример 3.4.3)). Матрицы, у которых число собственных векторов совпадает с порядком матрицы, называются диагонализируемыми. Диагонализируемыми, например, являются все симметричные матрицы. Матрицы, у которых число собственных вектором меньше, чем порядок матрицы, дефектными (это возникает в некоторых ситуациях при наличии кратных собственных чисел). Оба этих термина напрямую связаны с вопросом построения Жорданового разложения матрицы [10,16,25-29,40,64-65,69], который в настоящей Главе рассматриваться не будет.
Отметим, что если
– собственный вектор, то
– также является собственным вектором,
т.к.
.
Иными словами, собственный вектор
определен с точностью до множителя.
Рассмотрим произвольную диагонализируемую
матрицу
.
Пусть
– собственные числа матрицы
,
им соответствуют собственные вектора
,
т.е.
.
Поскольку собственный вектор
определен с точностью до множи-
теля, то всегда можно умножить его на
число
,
т.е. нормировать. Для нормированного
вектора
справедливо равенство:
.
(3.4.8)
Кроме того, векторы
образуют базис в
,
т.е. любой вектор
может быть представлен в виде их линейной
комбинации
.
(3.4.9)
Заметим также, что
.
(3.4.10)