1. Этап условной оптимизации.

На этом этапе находятся условные максимумы и условные оптимальные управления для каждого шага. Условный максимум на k-м шаге — это максимальный выигрыш, который будет получен при распределении остатка капиталовложений в размере x_k-1 между филиалами с номерами k, k+1, …, 3.

Формулы расчета условных максимумов для каждого шага, начиная с последнего, имеют следующий вид:

= f₃(u₃).

= {f₂(u₂) + f₃(u₃)},

= {f₁(u₁) + f₂(u₂) + f₃(u₃)},

Условные оптимальные управления являются решениями уравнений Беллмана, которые, начиная с последнего шага, имеют вид:

= f₃(u₃),

= ,

= .

Так как x₂ = x₁ – u₂ и x₁ = x₀ – u₁, то эти уравнения можно записать в более удобном для дальнейшего использования виде:

= f₃(u₃), (4.5)

= , (4.6)

= . (4.7)

Отметим, что на каждом шаге ищется максимум функции одной переменной, т.е. решается существенно более простая задача, чем исходная задача (4.1) – (4.4).

Найдем условные максимумы и условные оптимальные управления для каждого шага при всех возможных значениях остатков капиталовложений (параметров состояний) x_k. Согласно условиям задачи величина остатка на любом шаге — это некоторое число из множества {0, 10, 20, 30, 40}.

Найденные из уравнений Беллмана значения условных максимумов и условных оптимальных управлений для всех шагов будем сохранять в так называемой основной таблице 4.2.

Таблица 4.2. Основная таблица

Возможные значения остатков капиталовложений x	k = 1 (шаг 1)		k = 2 (шаг 2)		k = 3 (шаг 3)
0			0	0	0	0
10			10	6	10	4
20			10	10	20	7
30			10	13	30	8
40	20	15	20	15	40	10

Условную оптимизацию будем проводить, начиная с последнего третьего шага.

Шаг 3. Для всех значений x₂ ϵ{0, 10, 20, 30, 40} решается задача

= f₃(u₃).

Содержательный смысл решения этой задачи заключается в том, что определяется объем средств, который следует выделить третьему филиалу из наличного остатка х₂ для получения наибольшего выигрыша.

В этом случае решение находится совсем просто, так как анализ значений функции f₃(u), содержащихся в последнем столбце таблицы 4.1, показывает, что она является монотонно возрастающей. Это означает, что для любой величины остатка х₂ наибольший выигрыш будет достигнут, если все имеющиеся средства отдать третьему филиалу. Следовательно,

= х₂ и = f₃(х₂) для любого х₂ ϵ {0, 10, 20, 30, 40}.

Таким образом, в столбец основной таблицы 4.2 нужно занести значения из первого столбца, а в столбец — значения из последнего столбца исходной таблицы 4.1.

Шаг 2. Для всех значений x₁ ϵ{0, 10, 20, 30, 40} решается задача

= .

Содержательный смысл ее решения состоит в том, что определяется объем средств, который нужно выделить второму филиалу из наличного остатка х₁ для получения наибольшего суммарного выигрыша от второго и третьего филиалов. Для этого следует рассмотреть все допустимые варианты распределения капиталовложений между этими филиалами и выбрать наилучший вариант. Требуемые вычисления удобно проводить, используя следующую расчетную таблицу.

Таблица 4.3. Расчетная таблица для шага 2

1	2	3	4	5	6	7
x1	u2	x1 – u2	f2(u2)		f2(u2) +
0	0	0	0	0	0	0
10	0 10	10 0	0 6	4 0	4 6	6
20	0 10 20	20 10 0	0 6 8	7 4 0	7 10 8	10
30	0 10 20 30	30 20 10 0	0 6 8 9	8 7 4 0	8 13 12 9	13
40	0 10 20 30 40	40 30 20 10 0	0 6 8 9 12	10 8 7 4 0	10 14 15 13 12	15

В столбец 1 этой таблицы заносятся все возможные значения остатка x₁. Столбцы 2 и 3 содержат информацию обо всех допустимых вариантах распределения капиталовложений между вторым и третьим филиалами.

Столбцы 4 и 5 содержат выигрыши, которые будут получены от второго и третьего филиала при выделении им соответствующих денежных средств, а столбец 6 — их суммарный выигрыш.

Столбец 7 содержит значения получаемых условных максимумов, а соответствующие им условные оптимальные управления выделены в столбце 2 полужирным шрифтом.

Пусть, например, x₁ = 20. Возможны три варианта распределения этих средств между филиалами:

1. (0, 20) — второй филиал не получает ничего, а третий филиал получает 20 млн. руб. Суммарный выигрыш равен 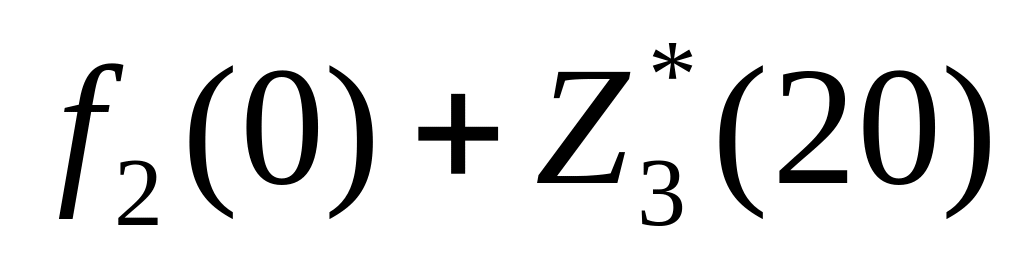= 0 + 7 = 7.

2. (10, 10) — каждый из филиалов получает по 10 млн. руб. Суммарный выигрыш равен 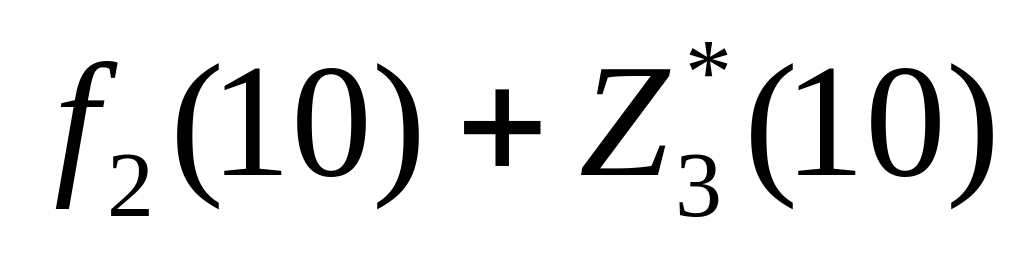= 6 + 4 = 10.

3. (20, 0) — второй филиал получает 20 млн. руб., а третий филиал не получает ничего. Суммарный выигрыш равен = 8 + 0 = 8.

Максимальный выигрыш равен max{7, 10, 8} = 10. Он достигается на втором варианте, т.е. при u₂ = 10. Значит, = 10 и = 10.

Найденные на этом шаге условные максимумы и условные оптимальные управления заносятся в соответствующие столбцы основной таблицы 4.2.

Шаг 1. На этом шаге решается задача

= .

при х₀ = 40. Содержательный смысл ее решения состоит в том, что определяется объем средств, который следует выделить первому филиалу для получения наибольшего суммарного выигрыша от всех трех филиалов. Для этого нужно рассмотреть все возможные варианты выделения средств первому филиалу и выбрать из них наилучший, исходя из того, что остаток средств распределяется между вторым и третьем филиалами оптимальным способом.

Результаты вычислений приведены в таблице 4.4, которая имеет такую же структуру, что и таблица 4.3, отличаясь от нее лишь «шапкой». Так как начальное состояние x₀ фиксировано, то в этом случае достаточно провести расчеты лишь при х₀ = 40.

Таблица 4.4. Расчетная таблица для шага 1

1	2	3	4	5	6	7
x0	u1	x0 – u1	f1(u1)		f1(u1)+
40	0 10 20 30 40	40 30 20 10 0	0 5 7 8 11	15 13 10 6 0	15 18 17 13 12	15

Полученные результаты = 15 и = 20 заносятся в таблицу 4.2. На этом этап условной оптимизации заканчивается.