Московский государственный институт электронной техники
(технический университет)
А. И. Литвинов
СБОРНИК ЗАДАНИЙ
для самостоятельной работы студентов
по курсу «Линейная алгебра»
Утверждено методическим советом каф. ВМ-2
Зав. кафедры С. Г. Кальней
МИЭТ, 2010 г.
—————————————————————————————————
Хочешь понять лучше – попробуй решать!!!
Сборник содержит систематизированный набор задач по основным разделам предмета «Линейная алгебра», преподаваемого на первом курсе факультета ЭТМО. Учитывается специфика факультета, направленность профессионального обучения будущих инженеров-технологов.
Хотя основная цель Сборника – предоставить студентам стандартный набор задач для самостоятельной доработки материала Предмета, по каждой теме представлена общая схема решения задачи и приведен частный пример применения общей схемы. Считаем важным также отработку принципов оформления материала по решённым задачам (домашние задания, контрольные работы и т.п.): инженер-технолог должен вырабатывать профессиональное восприятие оформления документа по любой разработанной им задаче-технологии.
СОДЕРЖАНИЕ:
Стр.
Часть 1. Аналитическая геометрия (АГ):
§ 1. Векторы. Операции с векторами. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
§ 2. Прямая на плоскости . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§ 3. Плоскость и прямая в пространстве . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Часть 2. Линейная алгебра (ЛА):
§ 4. Определители: вычисление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§ 5. Матрицы: операции с матрицами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
§ 6. Системы линейных уравнений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
§ 7. Линейные пространства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
§ 8. Линейные преобразования (операторы) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
§ 9. Квадратичные формы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
§ 10. Евклидовы пространства . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Терпенье и труд все перетрут!!!
§ 1. Векторы. Операции с векторами.
1.1. Дана система
векторов:
![]() ,
,![]() ,
,![]() ,
,
![]() .
Найти какой-нибудь
базис этой системы векторов и все
векторы системы, не входящие в этот
базис, выразить через векторы базиса.
.
Найти какой-нибудь
базис этой системы векторов и все
векторы системы, не входящие в этот
базис, выразить через векторы базиса.
Общие сведения. Базисом называют:
1*.
На прямой: любой ненулевой вектор
![]() .
Всякий вектор
,
лежащий на этой прямой, может быть
представлен в виде:
=
.
Всякий вектор
,
лежащий на этой прямой, может быть
представлен в виде:
=![]() ·
,
число
–
координата
относительно этого базиса.
·
,
число
–
координата
относительно этого базиса.
2*.
На плоскости: любая пара неколлинеарных
векторов
,
.
Всякий вектор
,
лежащий в этой плоскости, может быть
представлен в виде:
=
·
+![]() ·
,
числа
·
,
числа
![]() –
координаты
относительно этого базиса.
–
координаты
относительно этого базиса.
3*.
В пространстве: любые три вектора
,
,
,
если они не компланарны. Всякий вектор
![]() пространства
может быть представлен в виде линейной
комбинации векторов базиса:
=
·
+
·
+
пространства
может быть представлен в виде линейной
комбинации векторов базиса:
=
·
+
·
+![]() ·
,
где
,
,
–координаты
вектора
относительно этого базиса.
·
,
где
,
,
–координаты
вектора
относительно этого базиса.
Так как пространство можно рассматривать как общий случай 3-мерного пространства, а плоскость и прямую как частные случаи, то решать задачу будем для 3-мерных векторов.
Общая схема решения задачи:
1). Проверяем признак наличия базиса в заданной совокупности векторов.
2). Если базис
выделен, записываем линейную комбинацию:
=![]() ·
+
·
+![]() ·
+
·
+![]() ·
.
·
.
3). Решая систему уравнений, вычисляем неизвестные: , , .
4). Оформляем ответ.
Примеры (и образец оформления):
Пример-1*: Заданы векторы: =(1), =(3), =(2). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторой прямой, то признаком существования базиса является присутствие в совокупности векторов , , ненулевого вектора.
2). В качестве базиса примем вектор . Тогда можем записать: = · , = · .
3). Решаем уравнения: (3)= ·(1); (2)= ·(1), то есть уравнения: 3 = ·1; 2 = ·1, из чего следует: =3; =2.
Ответ: один из базисов: ; тогда: =3 , =2 .
Пример-2*: Заданы векторы: =(1,2), =(3,1), =(2,3). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторой плоскости, то признаком существования базиса является наличие в совокупности векторов , , хотя бы двух неколлинеарных векторов. В нашем случае среди заданных векторов нет коллинеарных. Это значит: любая пара векторов из заданной совокупности векторов может быть принята в качестве базиса.
2). В качестве базиса примем векторы и . Тогда можем записать: = · + · , то есть: ·(1,2)+ · (3,1)=(2,3). Используя свойства линейных операций с векторами, представим последнее равенство в виде: ( ·1+ ·3; ·2+ ·1)= (2,3), или в виде системы уравнений:
![]()
3). Решение системы
уравнений:
![]() .
Тогда можем записать:
=
.
Тогда можем записать:
=![]() .
.
Ответ: один из базисов: , ; тогда: = .
Пример-3*: Заданы векторы: =(3,1,2), =(1,3,1) , =(-1,2,4) , =(-2,4,7). Найти какой-нибудь базис этой системы векторов и выразить через него остальные векторы заданной системы векторов.
Решение:
1). Проверяем признак наличия базиса в заданной совокупности векторов. Так как из записи векторов следует, что все они принадлежат некоторому пространству, то признаком существования базиса является наличие в совокупности векторов , , , хотя бы трёх некомпланарных векторов. Так как векторы , неколлинеарные, то будем проверять тройки векторов , , и , , , используя понятие смешанного произведения:
=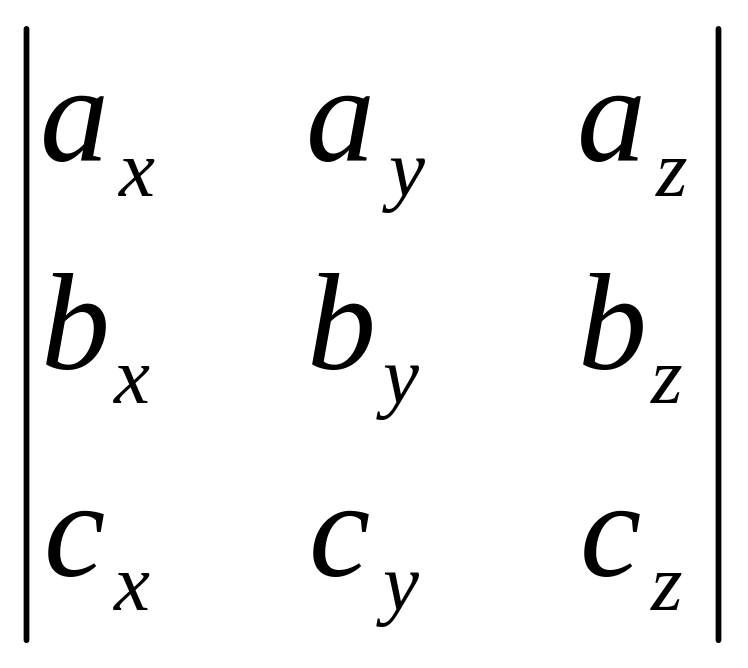 =
=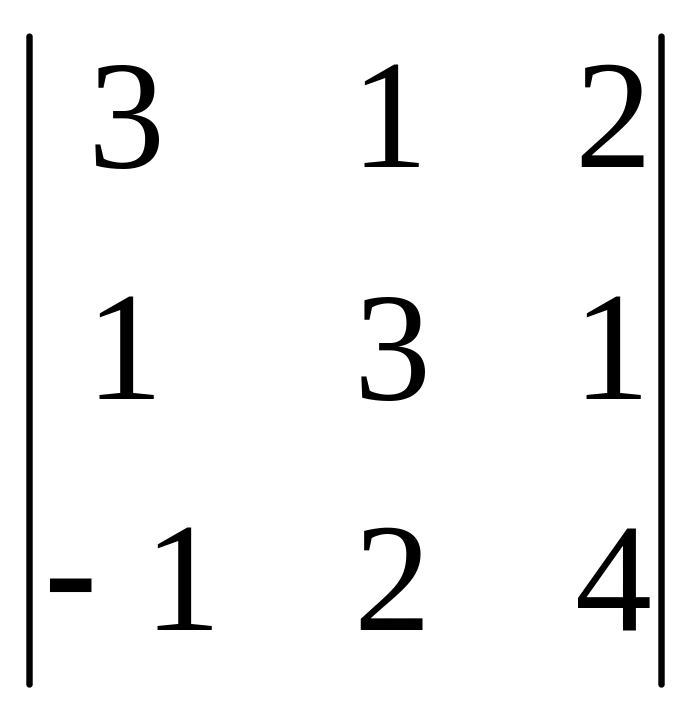 =
35
=
35![]() 0,
=
0,
=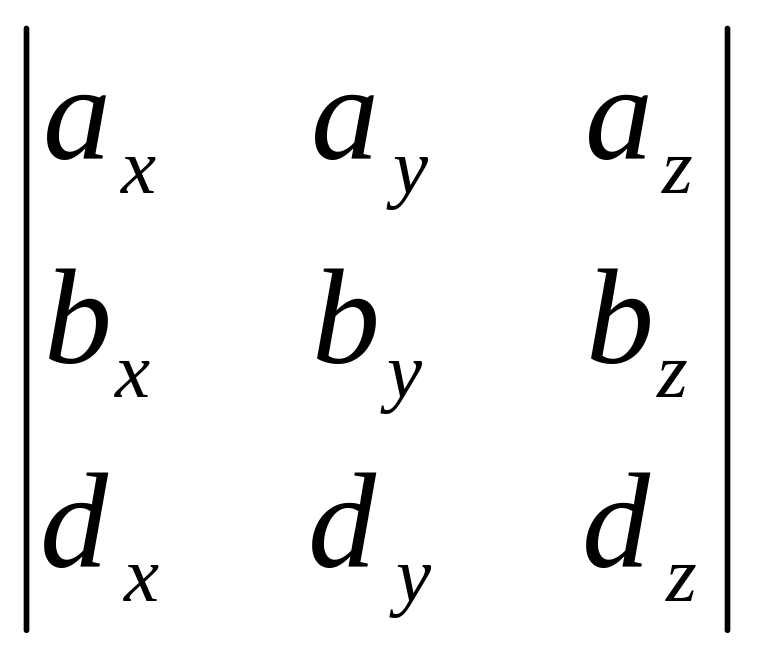 =
=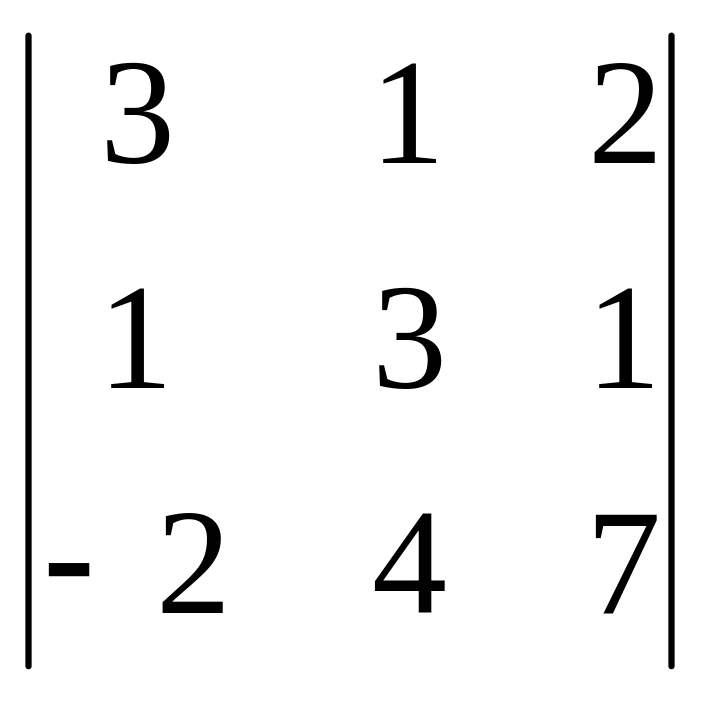 =
-40
0.
=
-40
0.
2). В качестве базиса может быть принята любая из троек векторов из заданной системы векторов. Примем в качестве базиса тройку векторы , , . Тогда можем записать: = · + · + · , то есть: ·(3,1,2)+ ·(1,3,1)+ ·(-1,2,4)=(-2,4,7). Используя свойства линейных операций с векторами, представим последнее равенство в виде: ( ·3+ ·1– ·1; ·1+ ·3+ ·2; ·2+ ·1+ ·4)=(-2,4,7), или в виде системы уравнений:
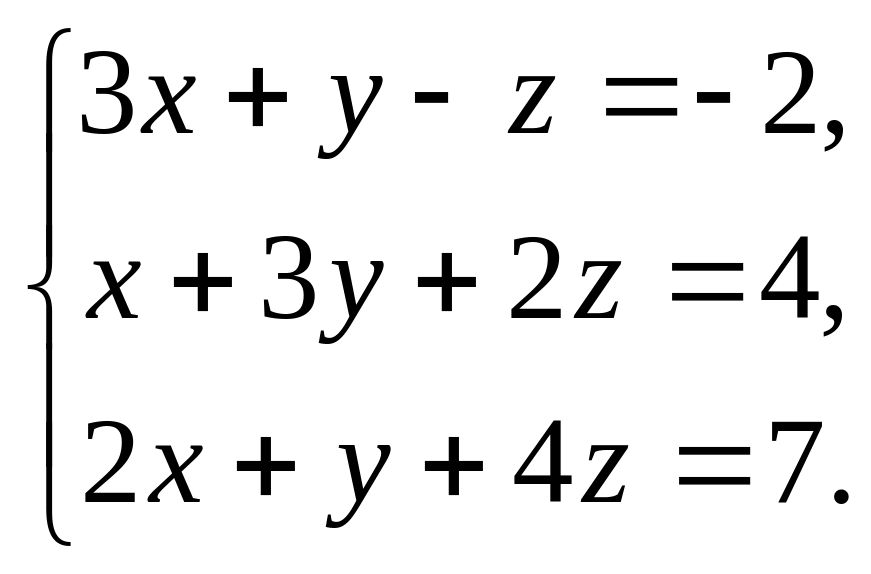
3). Решение системы:
![]() .
Тогда можем записать:
=
.
Тогда можем записать:
=![]() ·
+
·
+![]() ·
+
·
+![]() ·
.
·
.
Ответ: один из базисов: , , ; тогда: = · + · + · .
Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов) обязательно!
Варианты индивидуальных заданий:
Вар. |
Задание: |
Вар. |
Задание: |
1. |
=(3,1,2), =(1,3,1), =(-1,2,4), =(-2,4,7). |
16. |
=(2,3,1), =(2,2,3), =(4,1,2), =(8,0,5). |
2. |
=(1,3,0), =(2,-1,1), =(1,-1,2), =(6,12,-1). |
17. |
=(4,2,3), =(3,2,-1), =(4,1,2), =(3,1,8). |
3. |
=(2,1,-1), =(4,3,2), =(1,-1,1), =(1,-4,4). |
18. |
=(1,2,-1), =(3,0,2), =(-1,1,1), =(8,1,12). |
4. |
=(4,1,1), =(2,-1,-3), =(-1,2,1), =(-9,5,5). |
19. |
=(1,4,1), =(-3,2,0), =(1,-1,2), =(-9,-8,-3). |
5. |
=(-2,3,1), =(1,3,-1), =(2,4,1), =(-5,-5,5). |
20. |
=(2,1,-2), =(3,-1,1), =(4,1,0), =(-5,9,-13). |
6. |
=(5,1,1), =(2,-1,3), =(1,2,-1), =(13,,7). |
21. |
=(0,5,1), =(3,2,-1), =(-1,1,0), =(-15,5,6). |
7. |
=(3,2,1), =(-2,2,1), =(3,1,-1), =(6,12,-1). |
22. |
=(2,2,-1), =(0,-2,1), =(1,3,1), =(8,9,4). |
8. |
=(3,1,2), =(2,1,1), =(2,-1,4), =(3,-3,4). |
23. |
=(2,2,1), =(1,-2,0), =(-3,2,5), =(3,-4,0). |
9. |
=(4,2,1), =(-1,2,1), =(-1,1,2), =(3,3,-1). |
24. |
=(2,1,3), =(3,5,3), =(4,2,1), =(3,1,3). |
10. |
=(-1,2,1), =(2,1,3), =(1,1,-1), =(-1,7,4). |
25. |
=(2,3,1), =(1,-1,2), =(2,-1,0), =(-1,7,0). |
11. |
=(1,1,4), =(0,-3,2), =(2,1,-1), =(6,5,-14). |
26. |
=(1,-1,2), =(3,2,0), =(-1,1,1), =(11,-1,4). |
12. |
=(1,-2,0), =(1,1,3), =(1,1,4), =(6,-1,7). |
27. |
=(-1,1,2), =(0,3,2), =(1,-1,1), =(1,3,-1). |
13. |
=(1,0,5), =(-1,3,2), =(1,-1,1), =(5,15,0). |
28. |
=(2,1,3), =(-1,0,4), =(3,2,4), =(4,1,3). |
14. |
=(1,3,2), =(0,-1,2), =(3,3,4), =(2,-1,11). |
29. |
=(-3,2,4), =(-2,0,1), =(2,3,1), =(3,-2,0). |
15. |
=(1,-1,2), =(-1,0,1), =(2,5,-3), =(11,5,-3). |
30. |
=(5,1,3), =(0,1,2), =(-1,1,1), =(1,1,1). |
1.2. Заданы точки A,B,C,D в правой системе координат. Вычислить указанные в заданиях величины с точностью 0.001.
а)
проекцию вектора
![]() на вектор
на вектор
![]() ;
;
б) площадь треугольника ABC;
в)
объём тетраэдра
![]() .
.
Общие сведения: по всем представленным заданиям:
1). Для удобства
применения необходимых выражений
обозначим: A=![]() ,
B=
,
B=![]() ,
C=
,
C=![]() ,
D=
,
D=![]() .
Тогда можем записать выражения для
векторов, используемые во всех названных
задачах:
=B–A=
.
Тогда можем записать выражения для
векторов, используемые во всех названных
задачах:
=B–A=![]() =
=![]() ;
;
=D–A=![]() =
=![]() .
.
![]() =C–A=
=C–A=![]() =
=![]() .
.
2). Теперь приступим к решению задач, применяя формулы из общей теории.
а)*.
Заданы векторы
и
.
Требуется найти проекцию вектора
на направление, определяемое вектором
.
Из выражения для скалярного произведения
заданных векторов:
![]() проекция вектора
на направление
может
быть вычислена по формуле:
проекция вектора
на направление
может
быть вычислена по формуле:
![]() =
=![]() .
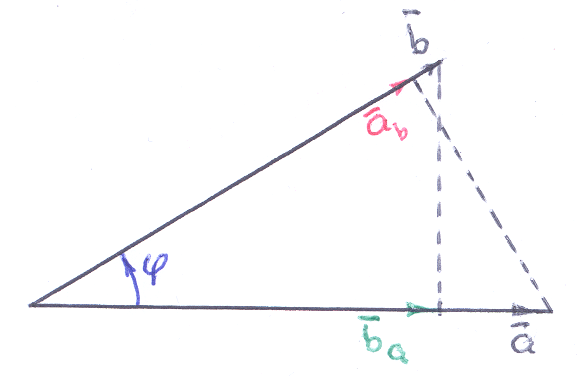
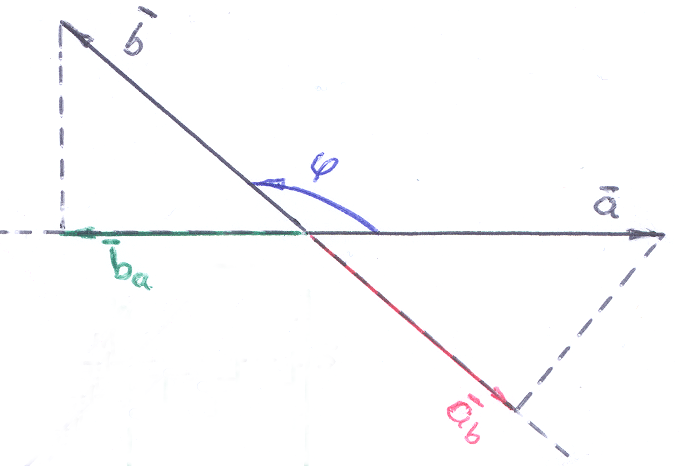
Рисунки иллюстрируют формулы:
.
Рисунки иллюстрируют формулы:
Для векторов,
заданных в координатной форме, запишем
необходимые для вычисления
![]() выражения:
выражения:
![]() =
=![]() ;
;
![]()
б)*.
Заданы векторы
и
.
Требуется найти площадь треугольника,
образованного векторами
и
.
Известно, что площадь параллелограмма,
заданного векторами
и
,
определяется выражением:
![]() ,
где
,
где
![]() – модуль векторного произведения
векторов
и
.
Для решаемой задачи это значит, что
площадь треугольника, построенного
на векторах
и
,
можно вычислять по формуле:
– модуль векторного произведения
векторов
и
.
Для решаемой задачи это значит, что
площадь треугольника, построенного
на векторах
и
,
можно вычислять по формуле:
![]() ,
где
,
где
![]() =
=![]() =
=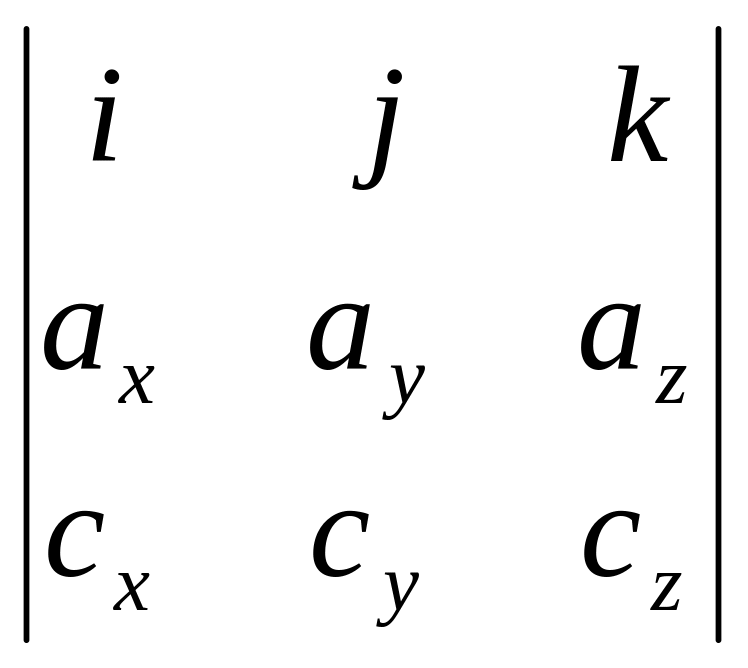 =
=![]() ∙
∙![]() –
–![]() ∙j
+
∙j
+![]() ∙k,
∙k,
где
![]() – единичные векторы, определяющие
направления осей правой прямоугольной
системы координат
– единичные векторы, определяющие
направления осей правой прямоугольной
системы координат
![]() .
.
в)*.
При вычислении объёма
![]() тетраэдра важно вспомнить, что
тетраэдра важно вспомнить, что
![]() ,
где
,
где
![]() – объём параллелепипеда. В задании
требуется вычислить объём
,
определяемого тремя векторами
,
,
.
Но этими же векторами определяется
параллелепипед, объём которого вычисляется
при помощи смешанного (векторно-скалярного)
произведения этих векторов. Для
иллюстрации используемых при решении
задачи формул удобно привести все
векторы к общей точке: так как векторы
свободные, то от этого они не изменяются.
На рисунке показаны все участвующие в
формулах элементы.
– объём параллелепипеда. В задании
требуется вычислить объём
,
определяемого тремя векторами
,
,
.
Но этими же векторами определяется
параллелепипед, объём которого вычисляется
при помощи смешанного (векторно-скалярного)
произведения этих векторов. Для
иллюстрации используемых при решении
задачи формул удобно привести все
векторы к общей точке: так как векторы
свободные, то от этого они не изменяются.
На рисунке показаны все участвующие в
формулах элементы.
И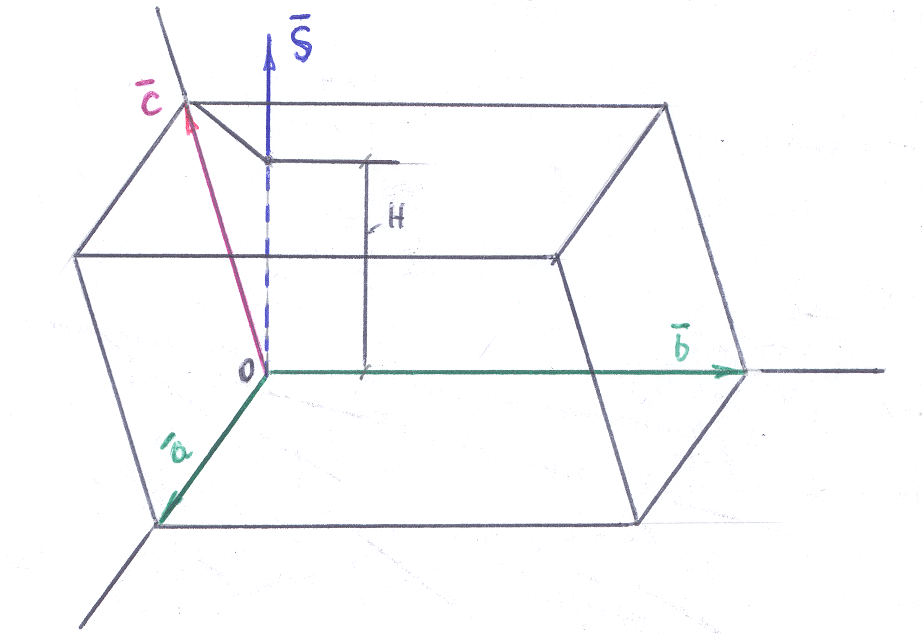 меем:
(
меем:
(![]() x
)∙
=
x
)∙
=![]() ∙
=
∙
=![]() ∙
∙![]() =
∙
=
∙![]() ,
где |
|=H,
причём
=H,
если тройка векторов – правая
и
=–H,
если – левая.
Из этой формулы следует: (
x
)∙
=V
–
объём параллелепипеда, но со
знаком.
,
где |
|=H,
причём
=H,
если тройка векторов – правая
и
=–H,
если – левая.
Из этой формулы следует: (
x
)∙
=V
–
объём параллелепипеда, но со
знаком.
Так как в задании требуется вычислить только объём, то независимо от того, какая тройка используется в вариантах задания, все используют формулу: |( x )∙ |=|V|.
Итак, имеем векторы , , . Вычисляем:
(
x
)∙
=![]() –
–![]() +
+![]() =
=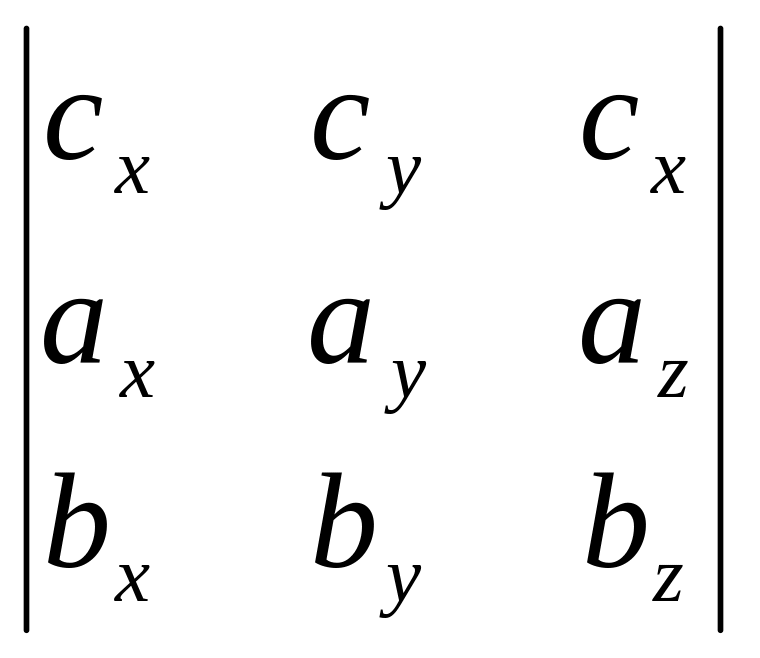 =
= .
.
Записываем
окончательную формулу:
=![]() |(
x
)∙
|.
|(
x
)∙
|.
Примеры (и образец оформления):
Общая
часть. Пусть имеем точки
A=
=(1,2,0),
B=
=(1,1,2),
C=
=(2,3,1),
D=
=(0,1,-1).
Построим векторы:
=B–A=
=![]() =
(0,-1, 2);
=
(0,-1, 2);
=D–A=
=![]() =(-1,-1,-1).
=(-1,-1,-1).
=C–A=
=![]() =(1,1,1);
=(1,1,1);
2). Теперь приступим к решению задач, применяя необходимые формулы.
Пример- а)*: Используем полученные векторы: =(0,-1,2), =(-1,-1,-1). Требуется найти проекцию вектора на направление, определяемое вектором .
Решение:
1). Воспользуемся формулой: = .
2). Вычислим:
=
=![]() =–1.
=–1.
3). Вычислим:
=![]() =
=![]() .
.
4). Вычислим:
=
=![]() =–
=–![]() =–0.577350269...
При заданной точности вычислений
примем:
=–0.577.
=–0.577350269...
При заданной точности вычислений
примем:
=–0.577.
Ответ: =–0.577.
Пример- б)*: Используем полученные векторы: =(0,-1,2), =(1,1,1). Требуется найти площадь треугольника, образованного векторами и .
Решение:
1). Общая формула:
,
где
=
=
=
∙
–
∙![]() +
∙
+
∙![]() .
.
2). Вычислим:
= =
=![]() ∙
–
∙
–![]() ∙
+
∙
+![]() ∙
=–3
+2
–
.
∙
=–3
+2
–
.
3). Вычислим:
![]() =
=![]() =
=![]() .
.
4). Вычислим:
![]() =
=![]() =1.87082869...
При заданной точности вычислений примем:
=1.87082869...
При заданной точности вычислений примем:
![]() =1.871.
=1.871.
Ответ: =1.871.
Пример- в)*: Заданы векторы: =(0,-1,2), =(-1,-1,-1) , =(1,1,1). В задании требуется вычислить объём тетраэдра , определяемого тремя векторами , , .
Решение:
1). Общая формула:
=![]() .
.
2). Вычислим:
![]() =
=
=
=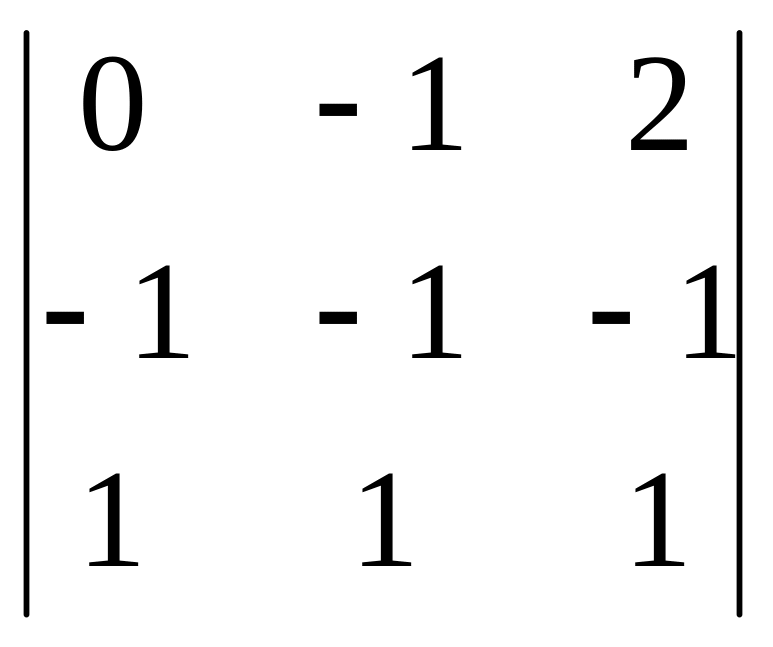 =0
– векторы
,
,
компланарны.
=0
– векторы
,
,
компланарны.
3). Вычислим: |( x )∙ |=0.
4). Вычислим: =0. При заданной точности вычислений примем: =0.000.
Ответ: =0.000.
Замечание: при оформлении задания использование рисунка (в карандаше, с использованием чертёжных инструментов) обязательно!
Варианты индивидуальных заданий:
Вар. |
Задание: |
Вар. |
Задание: |
1. |
A=(1,3,6),B=(2,2,1),C=(-1,0,1),D=(-4,6,3). |
16. |
A=(1,5,-7),B=(-3,6,3),C=(-2,7,3),D=(-4,8,-12). |
2. |
A=(-4,2,6),B=(2,-3,0),C=(-10,5,8),D=(-5,2,4). |
17. |
A=(-3,4,-7),B=(1,5,-4),C=(-5,-2,0),D=(2,5,4). |
3. |
A=(7,4,2),B=(7,-1,-2),C=(3,3,1),D=(-4,2,1). |
18. |
A=(-1,2,-3),B=(4,-1,0),C=(2,1,-2),D=(3,4,5). |
4. |
A=(2,1,4),B=(-1,5,-2),C=(-7,3,2),D=(-6,-3,6). |
19. |
A=(4,-1,3),B=(-2,1,0),C=(0,-5,1),D=(3,2,-6). |
5. |
A=(-1,-5,2),B=(-6,0,3),C=(3,6,-3),D=(-10,6,7). |
20. |
A=(1,-1,1)B=(-2,0,3),C=(2,1,-1),D=(2,-2,4). |
6. |
A=(0,-1,-1),B=(-2,3,5),C=(1,5,-9),D=(-1,-6,3). |
21. |
A=(1,2,0),B=(1,-1,2),C=(0,1,-1),D=(-3,0,1). |
7. |
A=(5,2,0),B=(2,5,0),C=(1,2,4),D=(-1,1,1). |
22. |
A=(1,0,2),B=(1,2,-1),C=(2,-2,1),D=(2,1,0). |
8. |
A=(2,-1,-2),B=(1,2,1),C=(5,0,-6),D=(-10,9,-7). |
23. |
A=(1,2,-3),B=(1,0,1),C=(-2,-1,6),D=(0,-5,-4). |
9. |
A=(-2,0,-4),B=(-1,7,1),C=(4,-8,-4),D=(1,-4,6). |
24. |
A=(3,10,-1),B=(-2,3,-5),C=(-6,0,-3),D=(1,-1,2). |
10. |
A=(4,4,5),B=(-5,-3,2),C=(-2,-6,-3),D=(-2,2,-1). |
25. |
A=(-1,2,4),B=(-1,-2,-4),C=(3,0,-1),D=(7,-3,1). |
11. |
A=(1,2,0),B=(3,0,-3),C=(5,2,6),D=(8,4,-9). |
26. |
A=(0,-3,1),B=(-4,1,2),C=(2,-1,5),D=(3,1,-4). |
12. |
A=(2,-1,2),B=(1,2,-1),C=(3,2,1),D=(-4,2,5). |
27. |
A=(-1,0,3),B=(4,2,1),C=(-3,-1,0),D=(4,1,5). |
13. |
A=(1,1,2),B=(-1,1,3),C=(2,-2,4),D=(-1,0,-2). |
28. |
A=(2,4,-2),B=(0,1,-3),C=(1,4,7),D=(-3,0,5). |
14. |
A=(2,3,1),B=(4,1,-2),C=(6,3,7),D=(7,5,-3). |
29. |
A=(-1,0,2),B=(3,7,1),C=(1,2,5),D=(-4,0,1). |
15. |
A=(1,1,-1),B=(2,3,1),C=(3,2,1),D=(5,9,-8). |
30. |
A=(2,3,4),B=(-5,1,0),C=(2,7,1),D=(-3,0,5). |