2.1. Понятие о точечных оценках и их свойствах

На практике встречаются ситуации, когда вид закона распределения уже известен и требуется найти только параметры, от которых он зависит. В частности, для нормального закона задача сводится к нахождению параметров m и , для закона Пуассона – параметра .

Пусть имеется некоторая СВ Х, закон распределения которой зависит от неизвестного параметра а. Требуется по результатам n независимых наблюдений СВ Х найти приближённое значение этого параметра. Искомое значение называется точечной оценкой параметра a и является случайной величиной, поскольку зависит от СВ , соответствующих n независимым измерениям СВ Х.

Точечная оценка параметра а называется состоятельной, если при неограниченном увеличении числа измерений n она сходится по вероятности к точному значению параметра а, т.е. . Оценка называется несмещённой, если , т.е. среднее значение оценки совпадает с точным значением параметра. Несмещённая оценка называется эффективной, если среди всевозможных несмещённых оценок параметра а она имеет наименьшую дисперсию.

Если свойство несмещённости (эфф-и) выполняется только в пределе при , то оценка называется асимптотически несмещённой (эфф-й).

2.2. Точечные оценки математического ожидания, дисперсии и среднего квадратического отклонения

Пусть Х СВ с и которые неизвестны. Результаты n независимых измерений СВ Х есть независимые случайные величины , при этом , , . За точечную оценку математического ожидания примем .

,

.

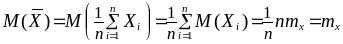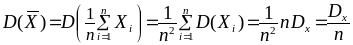Данная оценка математического ожидания является несмещённой, т.к. . В силу закона больших чисел (теорема Чебышева), эта оценка является состоятельной. Эффективность или неэффективность зависит от вида закона распределения СВ Х. Для произвольного закона эта оценка асимптотически эффективна, т.к. .

В качестве точечной оценки дисперсии может рассматриваться выборочная дисперсия . Доказывается, что , т.е. является асимптотически несмещённой оценкой дисперсии. В качестве несмещённой оценки используется (состоятельные и асимптотически эффективными).

3.1. Понятие о доверительных интервалах

Доверительный интервал - случайный интервал, который с заданной вероятностью , близкой к единице, содержит в себе неизвестный параметр распределения рассматриваемой СВ Х. .

3.2. Приближённый метод построения доверительного интервала для математического ожидания

Пусть – случайные величины, соответствующие результатам n независимых измерений произвольной СВ Х. независимы и одинаково распределены. Согласно центральной предельной теореме и замечанию к ней, при достаточно большом n закон распределения СВ близок к нормальному с математическим ожиданием и дисперсией . искать в виде , где величина определяется из условия .

Пусть . Учитывая вид и :

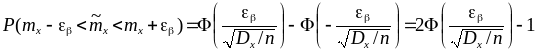
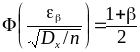, т.е. . За примем приближённое значения . Тогда , где .

3.3. Распределения “хи-квадрат”, Стьюдента и Фишера

Пусть – независимые СВ, имеющие стандартное нормальное распределение. Тогда распределение СВ называется “хи-квадрат” распределением с n степенями свободы. При любом имеет место . Для нахождения  из условия при различных значениях n и р составлены таблицы. Доказано, что , .

Случайная величина , где и СВ Х и независимы, называется дробью Стьюдента с n степенями свободы. При любом х имеет место равенство . Для нахождения  из условия при различных значениях n и р составлены таблицы. Имеет место и , причём при неограниченном увеличении n распределение СВ приближается к стандартному нормальному распределению.

Случайная величина 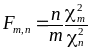, где и независимы, называется дробью Фишера с степенями свободы. При любом имеет место . Для нахождения  из условия при различных значениях m и n и близких к нулю значениях р составлены таблицы. В силу равенств

,

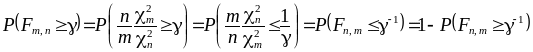при близких к единице значениях р соответствующее  можно найти из условия .