Парабола

Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой (предполагается, что фокус не лежит на директрисе).

Д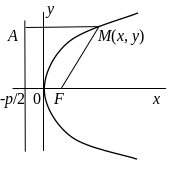 ля вывода уравнения параболы проведем ось абсцисс через фокус перпендикулярно директрисе, ось ординат поместим между фокусом и директрисой на одинаковом расстоянии от них. Расстояние от фокуса до директрисы обозначим через р, это число называется параметром параболы. Фокус будет иметь координаты F(p/2, 0) уравнение директрисы x = –p/2.

Уравнение параболы выводится из равенства

MF = MА.

После преобразований получаем уравнение

y² = 2px.

Парабола имеет ось симметрии, которая называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы. В отличие от гиперболы парабола не имеет асимптот.

Все параболы подобны друг другу. Значит, если сжать или растянуть параболу в любом направлении, получим подобную параболу.

Определение вида кривой второго порядка

По данному уравнению кривой второго порядка общего вида непонятно, какую кривую оно определяет. Чтобы выяснить это, уравнение требуется привести к каноническому виду с помощью преобразования координат. Если при этом используются только параллельные переносы и повороты, то определяется не только вид, но и все параметры кривой. Если же используется косоугольная система координат, то параметры искажаются, и мы сможем определить только вид кривой. Особым является случай, когда в уравнении кривой отсутствует произведение Вху. В этом случае преобразование координат основано на выделении полных квадратов, преобразование сводится к параллельному переносу, и параметры кривой сохраняются.

Пример 1.9.1. Определите вид и параметры кривой второго порядка, задаваемой уравнением 2x² – 3y² + 4x – 12y – 16 = 0.

Решение. а) Сначала выделим полные квадраты:

2(x² + 2x) – 3(y² – 4y) – 16 = 0;

2(x² + 2x + 1) – 2 – 3(y² – 4y + 4) + 12 – 16 = 0;

2(x + 1)² – 3(y – 2)² = 6.

Сделаем замену переменных: x + 1 = x₁, y – 2 = y₁:

2x₁² – 3y₁² = 6;

;

.

Получилось уравнение гиперболы с параметрами , , , .

Пример 1.9.1. Определите вид кривой второго порядка, задаваемой уравнением x² – 2xy + 3y² + 4x – 8y – 2 = 0.

Решение. а) Сначала произведем преобразование, позволяющее убрать член 2xy:

(x² – 2xy + y²) + 2y² + 4x – 8y – 2 = 0;

(x – y)² + 2y² + 4x – 8y – 2 = 0.

Делаем замену x – y = x₁, y = y₁, откуда x = x₁ + y₁:

x₁² + 2y₁² + 4(x₁ + y₁) – 8y₁ – 2 = 0;

x₁² + 2y₁² + 4x₁ – 4y₁ – 2 = 0;

(x₁² + 4x₁+ 4) – 4 + 2(y₁²– 2y₁ +1) – 2 – 2 = 0;

(x₁ + 2)² + 2(y₁ – 1)² = 8;

.

Получилось уравнение эллипса. Его параметры по полученному уравнению определить невозможно, так как в процессе преобразований они исказились.

У п р а ж н е н и я

1.9.1. Определите вид и параметры кривых второго порядка, заданных уравнениями: а) ; б) ; в) 2x² – 3y² = 12; г) x² – 4y = 0.

1.9.2. Напишите каноническое уравнение эллипса, если даны его полуоси a = 2, b = 5.

1.9.3. Составьте уравнение гиперболы, если ее вершины находятся в точках А₁(–3, 0) и А(3, 0), а фокусы в точках F₁(–5, 0) и F₂(5, 0).

1.9.4. Определите вид и параметры кривой второго порядка, заданной уравнением

а) x² – 2y² + 4x – 8y – 2 = 0;

б) 3x² + 2y² + 6x – 12y – 3 = 0.

1.9.4. Определите вид кривой второго порядка, заданной уравнением

а) x² – 4ху – 2y² + 4x – 12y – 3 = 0;

б) x² + 2ху + 2y² + 2x – 2y – 1 = 0;

в) x² + 2ху + y² + 4x – y – 2 = 0.