6.Векторная геометрия

В геометрическом векторном пространстве стандартный базис состоит из векторов, имеющих единичную длину, расположенных по координатным осям и направленных в положительную сторону соответствующих координатных осей. Векторы, соответствующие осям 0x, 0y, 0z, обозначают соответственно , , и называют основными или базовыми ортами.

Проекция вектора на прямую – это вектор, начало и конец которого есть проекции начала и конца вектора на эту прямую.

В разложении вектора = (₁, ₂, ₃) по базису: = ₁ + ₂ + ₃ слагаемые являются проекциями вектора на соответствующие координатные оси.

Векторы, параллельные одной прямой, называются коллинеарными; параллельные одной плоскости – компланарными.

Перпендикулярные векторы называют ортогональными.

Если = (a, b, c) и известны координаты точки A(x₁, y₁, z₁), то координаты точки B(x₂, y₂, z₂) находим сложением этих координат: x₂ = x₁ + a, y₂ = y₁ + b, z₂ = z₁ + c. Аналогично координаты начала вектора получаются из координат конца вычитанием координат вектора.

Пример 1.6.1. Найти координаты вершины D параллелограмма ABCD, если заданы координаты А(2, –1, 1), В(4, 2, 0), С(–3, 1, –2).

Р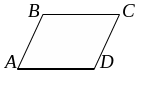 ешение. Изобразим параллелограмм ABCD на рисунке (не стараясь согласовывать положение вершин с их координатами), чтобы было наглядно видно, какие векторы использовать в вычислениях. Замечаем, что

= = (–3 – 4, 1 – 2, –2 – 0) = (–7, –1, –2),

и получаем координаты D(2 – 7, –1 – 1, 1 – 2), или D(–5, –2, –1).

Скалярное произведение

Скалярное произведение векторов и определяется формулой:

= cos, (1)

где  – угол между векторами и .

Свойства скалярного произведения:

1. = _.

2. = .

3. = .

4. .

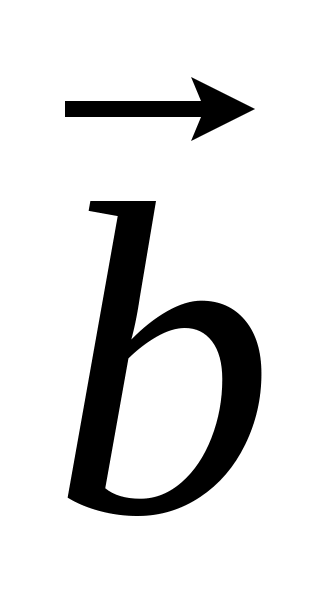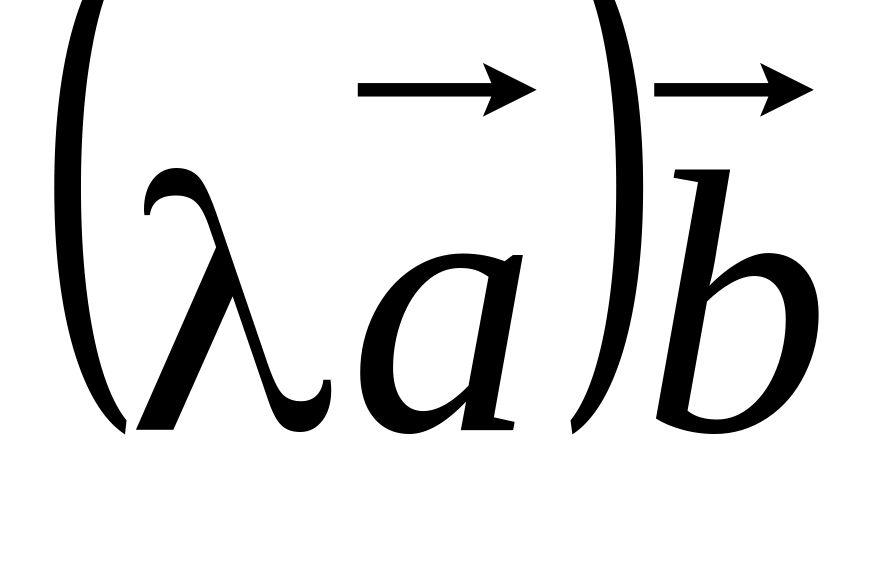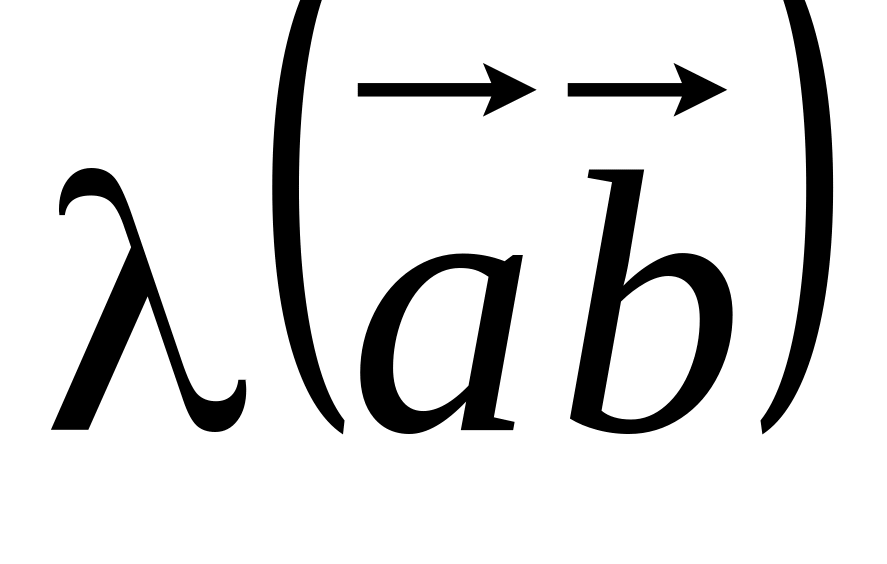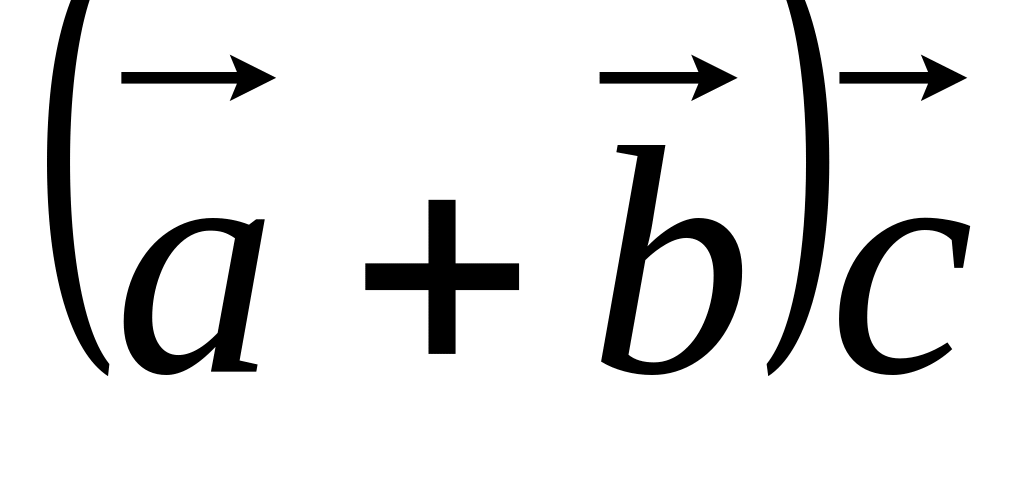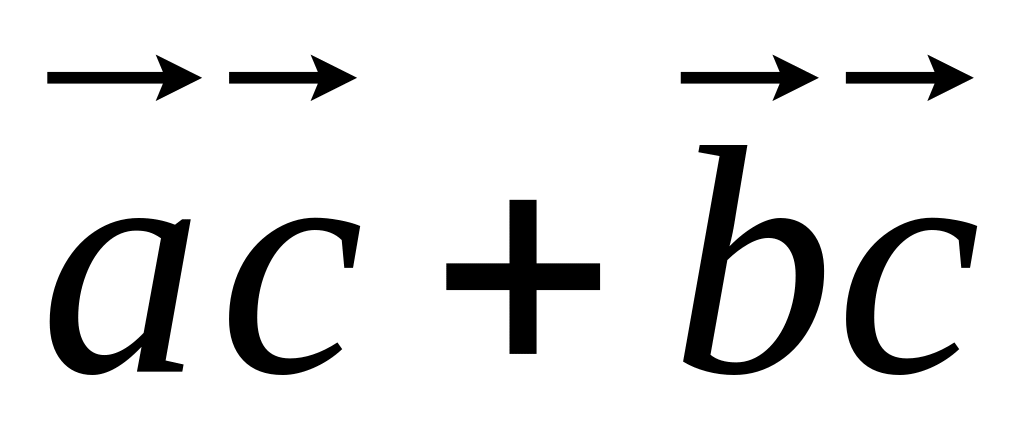5. Критерий ортогональности векторов: .

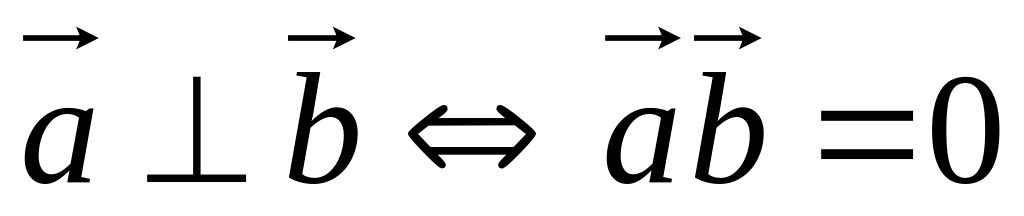6. Если = (a₁, a₂, a₃), 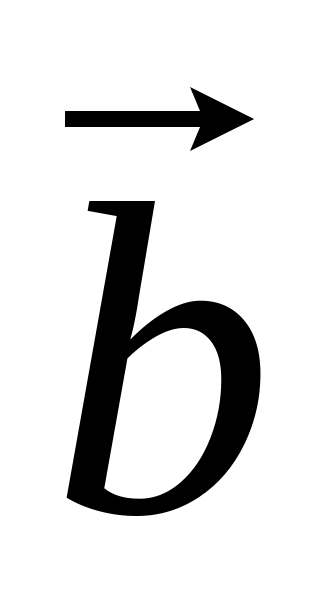= (b₁, b₂, b₃) то = a₁b₁ + a₂b₂ + a₃b₃. Такая же формула с двумя слагаемыми для плоского случая.

Пример 1.6.2. Найти косинус угла  между векторами = (2, –1, 3), и = (3, 2, –2).

Решение. Из формулы (1) получаем cos = ;

= = –2;

;

;

cos = .

Пример 1.6.3. Найти площадь треугольника АВС, если заданы координаты вершин А(2, –1, 3), В(3, 2, –2), С(0, 3, 1).

Решение. Площадь находим по формуле , где  – угол между АВ и АС. Вводим векторы

= (3 – 2, 2 – (–1), –2 – 3) = (1, 3, –5);

= (0 – 2, 3 – (–1), 1 – 3) = (–2, 4, –2).

cos находим, как в примере 1.6.2:

= –2 + 12 + 10 = 20;

; ;

cos = ;

;

.

Замечание. При вычислении sin сокращение не производилось специально, чтобы упростить вычисления на последнем шаге.

Векторное произведение

Упорядоченная тройка векторов , , пространства называется правой, если при совмещении их начал в одной точке из конца вектора поворот от к наблюдается против часовой стрелки. В противном случае тройка называется левой. Эта характеристика называется ориентацией тройки векторов.

Если векторы в тройке сдвинуть по кругу, то ориентация не изменится. Если же поменять местами два вектора, то ориентация изменится на противоположную.

Векторным произведением векторов и называется вектор =  такой, что:

(a) , где  – угол между векторами;

(b) , ;

(c) векторы , , образуют правую тройку.