9.Кривые второго порядка

Уравнение второго порядка – это уравнение вида

Ax² + Bxy + Cy² + Dx + Ey + F = 0.

Такое уравнение преобразованиями координат приводится к одному из следующих видов:

Уравнение	Фигура
	Эллипс
	Точка
	Пустое множество (мнимый эллипс)
	Гипербола
	Пара пересекающихся прямых
y2 = 2px, p>0	Парабола
y2 = а2, а  0	Пара параллельных прямых
y2 = –а2, а  0	Пустое множество (пара мнимых параллельных прямых)
y2 = 0	Прямая (пара совпавших прямых)

Эллипс

Эллипсом называется множество точек плоскости, для каждой из которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

В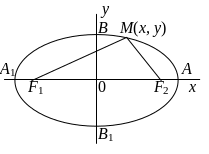 ыведем уравнение эллипса. Для этого расположим координатные оси так, чтобы фокусы F₁ и F₂ располагались на оси абсцисс симметрично относительно начала координат. Пусть расстояние между ними равно 2с, значит, они имеют координаты F₁(–с, 0) и F₂(с, 0). Пусть M(x, y) – произвольная точка эллипса. Тогда из определения эллипса получаем уравнение

MF₁ + MF₂ = 2a.

Подставляем MF₁ = , MF₂ = , получаем

+ = 2а.

Это уравнение приводится к виду

(a² – c²)x² + a²y² = a²(a² – c²).

При этом a >c, поэтому a² – c² > 0, и можно ввести обозначение a² – c² = b². Уравнение тогда приводится к виду b²x² + a²y² = a²b². Разделив его на a²b², получим каноническое уравнение эллипса

.

Эллипс симметричен относительно координатных осей и пересекает ось абсцисс в точках А₁(–с, 0) и А(с, 0), ось ординат в точках B₁(–b, 0) и B(b, 0). Эти четыре точки называются вершинами эллипса. Отрезок А₁А называется большой осью эллипса, отрезок В₁В – малой осью. Таким образом, а и b – это длины большой и малой полуосей.

Эксцентриситетом эллипса называется число . Для любого эллипса . Эксцентриситет характеризует степень сжатия эллипса: чем ближе эксцентриситет к 1, тем сильнее сжат эллипс. При = 0 эллипс является окружностью. При этом фокусы эллипса сливаются в одну точку, совпадающую с центром эллипса.

Гипербола

Гиперболой называется множество точек плоскости, для каждой из которых разность расстояний до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а.

У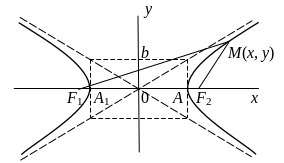 равнение гиперболы выводится аналогично уравнению эллипса из равенства

MF₁ – MF₂ = 2a.

Здесь фокусы имеют координаты F₁(–с, 0) и F₂(с, 0), c > b и c² – a² = b². После преобразований получаем уравнение

.

Гипербола симметрична относительно обеих координатных осей. Она состоит из двух ветвей. Гипербола пересекает ось абсцисс в двух точках А₁(–а, 0) и А(а, 0), которые называются вершинами гиперболы.

Прямые называются асимптотами гиперболы. Они могут строиться с помощью четырех прямых, параллельных осям: х = а, у = b. В пересечении этих прямых образуется прямоугольник, который называется основным прямоугольником гиперболы.

Эксцентриситетом гиперболы называется число . Для любой гиперболы > 1. Эксцентриситет характеризует степень сжатия гиперболы: чем ближе эксцентриситет к 1, тем сильнее вытянут основной прямоугольник гиперболы.