Фрагмент таблицы критических точек распределения “хи-квадрат”

l	1 2 3 4 5 6 ….
0.010 0.025 0.050 . . .	9.2 11.3 13.3 … 5.0 7.4 … 3.8 6.0 … …

Расчетное значение χ² сравнивают с найденной из таблицы (см. табл. 1.2) критической точкой χ²_кр(α, l). Если χ²< χ²_кр(α, l), то гипотезу о том, что закон распределения случайной погрешности Δ имеет вид р(Δ), принимают. В противном случае эта гипотеза отвергается, и либо повторяют заново измерения, либо выдвигают другую гипотезу, которую также проверяют.

О сновным недостатком экспериментального определения функции р(Δ) является большая трудоемкость эксперимента. Для сравнительно точного определения р(Δ) число измерений должно быть достаточно велико. В частности, для каждого интервала m_j должно быть не менее от 5 до 10. Для получения же достаточно точных значений и требуется гораздо меньше измерений (практически достаточно произвести лт 10 до 20 измерений).

7. Обработка результатов косвенных измерений.

При косвенных измерениях абсолютная погрешность измеряемой величины ΔY является некоторой функцией погрешностей прямых измерений

ΔY=F(ΔX₁, ΔX₂,…, ΔX_n)

В простом случае при одной переменной Y=f(X) в результате измерения получаем

Y+ ΔY=f(X+ ΔX)

Разложим правую часть последнего соотношения в ряд Тейлора и отбросим члены разложения высшего порядка малости

Y+ ΔY=f(X)+[df(X)/dX] ΔX .

Отсюда абсолютная погрешность

ΔY=[df(X)/dX] ΔX .

и относительная погрешность

Аналогично в общем случае, когда Y=f(X₁, X₂,…,X_n), абсолютная погрешность результата косвенных измерений ΔY=ⁿ_i=1A_i ΔX_i , где A_i=Y/X_i - коэффициенты влияния погрешностей ΔX_i на погрешность результата косвенных измерений (А≤≥0), и относительная погрешность

, где B_i =(Y/X_i)(X_i/Y) - коэффициенты влияния погрешностей γ_Хi на погрешность результата косвенных измерений (В_i≤≥0).

Величины A_i и B_i могут быть найдены аналитически при известной функциональной зависимости Y=f(X₁,X_2,…X_n), численным дифференцированием на ЭВМ (Y/X_i∆Y/∆X_i), а также по результатам физического эксперимента.

Е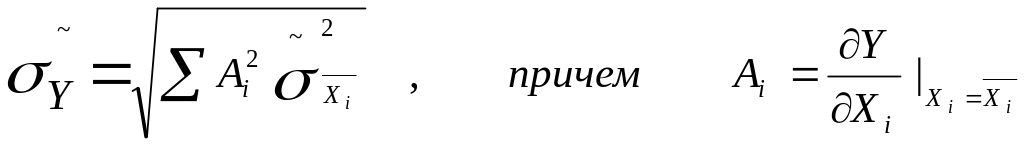 сли X₁, X₂,…,X_n измеряются статистическим методом, т.е. в результате многократных наблюдений определяются их действительные значения и среднеквадратичные отклонени, то для оценки среднеквадратичного отклонения результата косвенных измерений применяют закон накопления частных погрешностей

Е сли в результате прямых измерений отсутствуют систематические погрешности, то результат косвенного измерения ищется по формуле

П ри этом, строго говоря, Y≠ .

1.9.Обработка результатов совместных измерений.

Пусть необходимо экспериментально исследовать зависимость между физическими величинами x и y и получить её аналитическое выражение на основе опытных данных в виде y=f (x,c₁,c₂,…,c_k), где c₁,c₂,…,c_k – числовые параметры. В результате n независимых наблюдений можно получить n экспериментальных точек с координатами x_i, y_i, причем n>k. По совокупности точек (x_i, y_i), размещенных на координатной плоскости XOY, выдвигается гипотеза о конкретном виде аппроксимирующей функции f (например, логарифм, экспонента, арктангенс и т.п.).

Эта функция должна удовлетворять двум противоречивым требованиям: её выражение должно быть как можно более простым, но с другой стороны аппроксимация должна быть максимально точной. Прохождение аппроксимирующей функции через все экспериментальные точки может быть обеспечено путем использования кусочно-линейной зависимости или полинома высокой степени (интерполяционный метод), однако при этом, несмотря на кажущийся идеальный результат, требуемая точность не достигается (точки (x_i; y_i) получены с некоторыми неизбежными погрешностями, и прохождение аппроксимирующей функции y=f(x) через каждую из них совсем не обязательно).

В торым этапом аппроксимации после выявления конкретного вида функции f является определение значений числовых параметров c₁,c₂,…,c_k. Они могут быть найдены интерполяционным методом, который заключается в составлении системы из k уравнений, неизвестными в которых являются данные числовые параметры, следующей структуры:

Однако данный метод хотя и прост в реализации, но не обеспечивает, как уже отмечалось выше, высокой точности аппроксимации всей зависимости в целом.

Н аиболее точное решение данной задачи обеспечивается методом наименьших квадратов (МНК), который формулируется следующим образом: наилучшим взаимным расположением экспериментальных точек и аппроксимирующей кривой следует считать такое, при котором сумма квадратов расстояний по оси Y от точек до кривой минимальна

Д ля максимально точной аппроксимации надо

И ли

Причем значения производных f/c₁,…,f/c_k за знак суммы выноситься не могут, т.к. вычисляются поочередно в экспериментальных точках x_i . Решением полученной по МНК системы уравнений являются искомые значения c₁,c₂,…,c_k , удовлетворяющие условию D=min.

П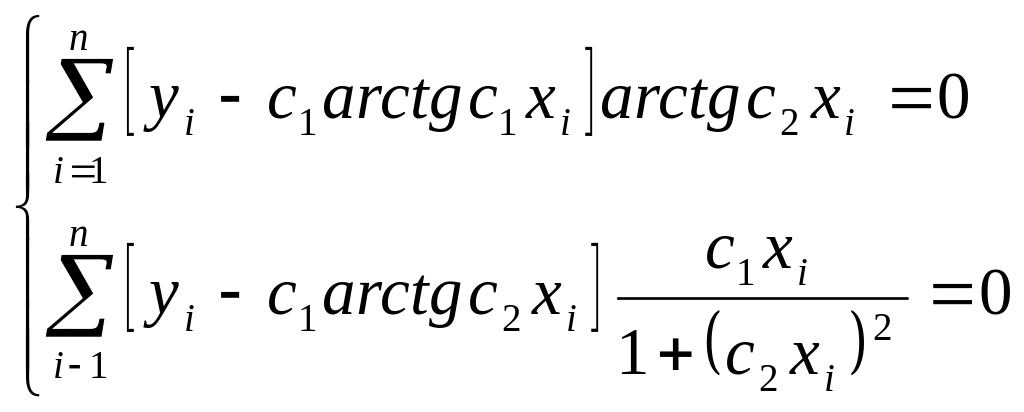 усть y=c₁arctg c₂x.Тогда система уравнений по МНК имеет вид

И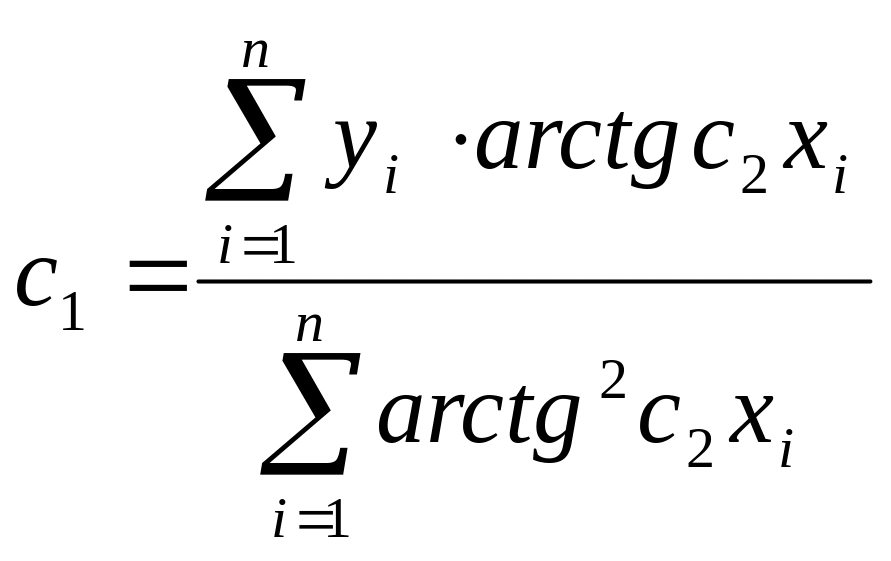 з первого уравнения выразим неизвестную с₁

и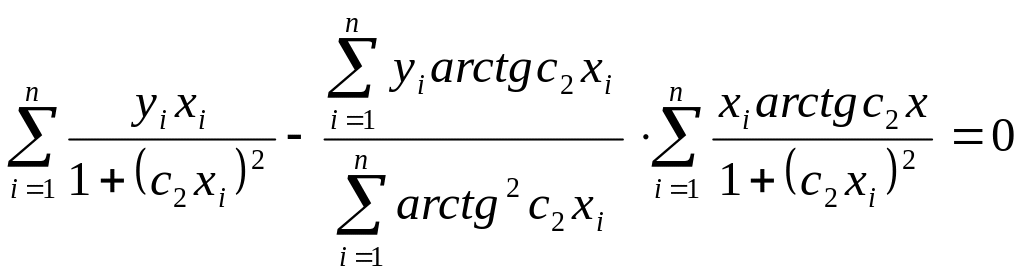 подставим во второе уравнение

Последнее выражение является достаточно сложным трансцендентальным уравнением относительно одной неизвестной с₂

F(c₂) = 0 ,

причем в явном виде оно не разрешается и может быть разрешено лишь численно на ЭВМ, в частности, методом простого перебора. Блок-схема соответствующего алгоритма изображена на рис. 1.6, где приняты следующие обозначения: с^* - начальное значение корня, ∆с – шаг перебора, ε – точность вычислений функции вблизи корня.

Аналогично могут быть найдены числовые параметры любых других аппроксимирующих функций.

Рис. 1.6. Блок- схема алгоритма решения на ЭВМ трансцендентных уравнений методом простого перебора.