
- •Введение.
- •Единицы измерения.
- •Классификация погрешностей измерения.
- •Оценка случайных погрешностей.
- •Фрагмент табулированной зависимости φ(k)
- •Оценки параметров распределения случайной погрешности.
- •X является оценкой матожидания м[х] измеряемой величины. При отсутствии систематических погрешностей оно принимается за истинное. Относительно X рассеиваются результаты измерений.
- •Pис. 1.4. Блок-схема алгоритма обработки результатов измерений.
- •Обработка результатов прямых измерений.
- •Фрагмент таблицы критических точек распределения “хи-квадрат”
- •Обработка результатов косвенных измерений.
- •1.9.Обработка результатов совместных измерений.
- •Пособы суммирования погрешностей.
- •1.11. Классификация средств измерения.
- •1.12. Основные свойства средств измерений.
- •Цифро-аналоговые преобразователи.
- •Аналого-цифровые преобразователи.
- •Функциональная схема;
- •Уровни сигналов на выходах сс следящего ацп.
- •Цифровые вольтметры.
- •2.5. Измерение частоты периодических колебаний.
- •2.6. Измерение периода электрических сигналов.
- •2.7.Измерение сдвига фаз.
- •2.8. Измерение коэффициента гармоник.
- •2.9. Измерительные генераторы сигналов.
Оценка случайных погрешностей.
Задача оценки погрешности результата измерения состоит в том, чтобы указать границы возможного изменения погрешности результата измерений при повторных измерениях. Наиболее полной характеристикой случайной погрешности как и любой случайной величины является закон распределения вероятности её появления.
В большинстве случаев в качестве такого
закона используется закон
нормального распределения
(закон Гаусса)
(рис. 1.2)
большинстве случаев в качестве такого
закона используется закон
нормального распределения
(закон Гаусса)
(рис. 1.2)
Где х – i-ый результат измерения, М[Х] – математическое ожидание измеряемой величины, относительно которого рассеиваются результаты измерения и которое при отсутствии систематических погрешностей принимается за истинное значение измеряемой величины; ∆=х-М[Х]; σ – среднеквадратичное отклонение (разброс) х относительно М[Х] (или ∆ относительно нуля).
З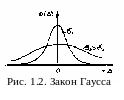 акон
Гаусса основан на предположении, что
случайные погрешности подчинены
следующим закономерностям:
акон
Гаусса основан на предположении, что
случайные погрешности подчинены
следующим закономерностям:
а) равные по абсолютному значению погрешности (+∆ и минус ∆) равновероятны;
б) малые по абсолютному значению погрешности более вероятны, нежели большие;
в) Вероятность появления случайных погрешностей, превосходящих по модулю некоторое определенное число (предел возможной погрешности), практически равна нулю.
Д![]() исперсия
D
случайной погрешности, равная дисперсии
результатов измерений, представляет
собой матожидание квадрата случайной
погрешности и характеризует разброс
результатов измерения из-за наличия
случайных погрешностей
исперсия
D
случайной погрешности, равная дисперсии
результатов измерений, представляет
собой матожидание квадрата случайной
погрешности и характеризует разброс
результатов измерения из-за наличия
случайных погрешностей
![]()
На практике удобнее пользоваться величиной , имеющей размерность случайной величины. С уменьшением σ (см. рис.1.2) растет число малых погрешностей и, значит, увеличивается степень приближения к истинному значению измеряемой величины.
Вероятность попадания случайной погрешности в некоторый заданный интервал между ∆ 1 и ∆ 2 определяется выражением

Н![]() а
практике широко применяется нормированное
нормальное распределение,
которое получается при переходе к
случайной величине k= ∆/σ. Для него
заранее просчитаны (табулированы)
значения доверительной вероятности Р
(вероятности попадания нормированной
случайной величины в диапазон от минус
k
до +k)
в соответствии с выражением
а
практике широко применяется нормированное
нормальное распределение,
которое получается при переходе к
случайной величине k= ∆/σ. Для него
заранее просчитаны (табулированы)
значения доверительной вероятности Р
(вероятности попадания нормированной
случайной величины в диапазон от минус
k
до +k)
в соответствии с выражением
Следовательно, для характеристики случайных погрешностей ∆ надо найти σ и k. Величина k определяется задаваемой доверительной вероятностью (табл. 1.1).
Таблица 1.1
Фрагмент табулированной зависимости φ(k)
Ф = P |
… |
0,5 |
0,68 |
0,95 |
0,98 |
0,99 |
0,997 |
k |
… |
0,667 |
1 |
2 |
2,33 |
2,58 |
3 |
Д ля оценки случайных погрешностей кроме среднеквадратичного отклонения ∆1, 2= ± σ используют также срединную погрешность ряда измерений ∆1,2 =±(2/3)σ появление случайных погрешностей в пределах и за пределами интервала (2/3)σ равновероятно и равно 50%) и наибольшую возможную погрешность ∆1,2 = (2/3)σ (вероятность появления случайных погрешностей, больших по модулю 3σ , составляет 0,3%, а меньших – 99,7%). Интервал ±3σ в случае нормального распределения представляет собой интервал достаточно достоверного результата измерения. При практических измерениях появление погрешности, большей по модулю 3σ, почти исключено.
В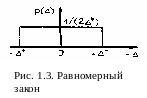 измерительной практике распространен
также равномерный
закон распределения плотности вероятности
случайной погрешности (рис. 1.3), при
котором функция р(∆) постоянна внутри
интервала [-∆
*,
+∆
* ]
и равна нулю вне его.
измерительной практике распространен
также равномерный
закон распределения плотности вероятности
случайной погрешности (рис. 1.3), при
котором функция р(∆) постоянна внутри
интервала [-∆
*,
+∆
* ]
и равна нулю вне его.
