6. Оценки параметров распределения случайной погрешности.

Основными параметрами распределения случайной погрешности являются матожидание и среднеквадратичное отклонение. Точно их можно найти только при бесконечно большом числе измерений. Практически же число измерений n всегда ограничено. Поэтому на практике находят приближенные оценки параметров.

Оценки должны быть состоятельными, несмещенными и эффективными. Если при увеличении n оценка приближается к значению оцениваемого параметра, то она состоятельная. Если матожидание оценки равно оцениваемому параметру, то она несмещенная. Если дисперсия оценки меньше дисперсии любой другой оценки данного параметра, то она эффективная.

П усть проведено n равноточных измерений значения некоторой физической величины x. Наиболее достоверным значением, которое можно приписать измеряемой величине, является среднее арифметическое

X является оценкой матожидания м[х] измеряемой величины. При отсутствии систематических погрешностей оно принимается за истинное. Относительно X рассеиваются результаты измерений.

О тклонение результата каждого измерения от X (по величине и знаку) определяется выражением

где V_i – остаточные погрешности.

С войства остаточных погрешностей:

,(при данном X ).

П о сумме квадратов всех остаточных погрешностей определяют наиболее широко используемую оценку влияния случайной погрешности на результат измерения – оценку среднеквадратичного отклонения  :

О ценка  характеризует точность ряда измерений и степень рассеяния результата измерений вокруг среднего арифметического.

Т.к. среднее арифметическое само обладает некоторой случайной погрешностью, то вводится понятие оценки среднеквадратичного отклонения среднего арифметического:

т оже характеризующее погрешность результата измерения.

Р ассмотренные оценки результата измерения, выражаемые одним числом, называются точечными оценками. Эти оценки неполные, поскольку _х указывает на границы интервала, в котором может находиться истинное значение Х₀, но ничего не говорит о вероятности попадания Х₀ в этот интервал.

При интервальной оценке определяется доверительный интервал, между границами которого с определенной вероятностью находится истинное значение Х₀. Задавшись значением доверительной вероятности Р при нормальном распределении случайных величин и бесконечно большом числе измерений n→∞, по таблицам Ф(k) (см. табл. 1.1) находят значение k, а затем и доверительный интервал ∆_{1, 2} =k _х .

П ри 2≤n<20 размер доверительного интервала увеличивается и определяется с помощью распределения Стьюдена. Результат измерения с интервальной оценкой записывается в виде:

Т.е. отклонение среднего арифметического от истинного значения измеряемой величины не превышает ∆_{1, 2} с вероятностью Р.

П ри обработке результатов измерений определяется относительная квадратичная погрешность результата измерения

Окончательно обобщенная блок-схема алгоритма обработки результатов измерений имеет вид (рис. 1.4):

Pис. 1.4. Блок-схема алгоритма обработки результатов измерений.

Таким образом, основная форма представления результатов измерения имеет вид:

Х₀= X ± ∆_{1, 2} ; Р=…, что предусмотрено действующими стандартами и методическими указаниями.

7. Обработка результатов прямых измерений.

По способу получения результата различают прямые, косвенные и совместные измерения. Прямыми называют измерения, при которых искомое значение величины находят непосредственно из опытных данных (например, измерение тока амперметром). Косвенными называют измерения, при которых искомое значение величины Y находят на основании известной зависимости между этой величиной и величинами Х₁, Х₂, …, Х_n, подвергаемыми прямым измерениям (например, измерение мощности путем прямого измерения тока и напряжения с последующим вычислением P=UI). Совместными называются производимые одновременно измерения двух или нескольких величин для нахождения зависимости между ними.

О бработка результатов прямых измерений кроме определения величин и ∆_{1, 2} ставит своей целью также выявление конкретного вида закона распределения вероятности появления случайной погрешности р(∆). Для этого производят многократные независимые измерения одной и той же величины х, получая ряд значений х_i , i= . Этому ряду соответствует ряд погрешностей ∆_i=x_i- , i= .

З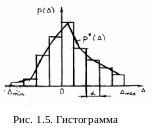 атем строится гистограмма (рис. 1.5) – ступенчатая кривая, соответствующая экспериментальной зависимости р(∆). Для её построения весь диапазон значений ∆_i от ∆_min до ∆_max делят на одинаковые интервалы, число которых находят по правилу Старджесса

N = 1+3,3 lg n

Т огда ширина каждого интервала определится в соответствии с выражением

После этого находят число значений m_j случайной погрешности ∆, приходящееся на каждый j-ый интервал. Тогда частоту

(статистическую вероятность) попадания ∆ в j-ый интервал можно вычислить как

Р_j^* =m_j/n .

По оси абсцисс откладывают непосредственно значения ∆. Над каждым конечным отрезком оси абсцисс, соответствующим j-му интервалу, строится прямоугольник, площадь которого с учетом масштабов по осям равна величине Р_j^*. Для этого необходимо, чтобы высота каждого j-го прямоугольника равнялась Р_j^*/α . В результате общая площадь гистограммы численно равна единице.

С помощью гистограммы строят так называемый практический закон распределения вероятности р^* (∆), называемый полигоном, для чего последовательно соединяют отрезками прямых середины верхних сторон всех прямоугольников гистограммы.

Искомый теоретический закон распределения может быть найден в результате подбора некоторой аналитической функции, соответствующей внешнему виду гистограммы или полигона, с тем, чтобы графики теоретического и практического законов максимально точно совпадали бы во всем диапазоне изменения ∆.

В ыбранная функция р(∆a,b,c,…), где а,b,c – некоторые числовые параметры, должна удовлетворять основным свойствам законов распределения:

Д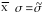 ля окончательного определения теоретического закона распределения надо найти значения a,b,c,…. В соответствии с методом моментов эти значения должны быть такими, чтобы основные числовые характеристики (моменты) теоретического закона совпадали с соответствующими статистическими характеристиками практического распределения, т.е. М[Х]= , и т.д.

Д ля оценки степени соответствия практического и теоретического законов распределения применяют критерий согласия Пирсона (“хи-квадрат”). Для этого вычисляют величину

где Р_j – вероятность попадания ∆ в j-й интервал, найденная по теоретическому закону.

Для упрощения расчетов Р_j находят не интегрированием, а приближенно

P_j = P(∆_ср.j)d ,

где р(∆_ср.j) – значение теоретического закона распределения в точке ∆_ср.j =(∆_j+∆_j+1)/2; ∆_j и ∆_j+1 –границы j-го интервала.

Чем меньше χ², тем ближе теоретический закон к практическому. В случае их полного совпадения χ²=0. Граничное значение χ²_кр, разделяющее области принятия и непринятия гипотезы о том, что случайная величина ∆ распределена по найденному закону р(∆), определяют по таблице критических точек распределения “хи-квадрат” (табл. 1.2), в которой приняты следующие обозначения: α – уровень значимости, численно равный вероятности признания справедливой гипотезы неверной (ошибка 1 рода)(величину α обычно выбирают близкой к нулю), l – число степеней свободы, определяемое из выражения

l = N-r-1 ,

Где r – количество числовых параметров теоретического закона, оцененных по результатам измерений (так, для нормального закона l=N-3).

Таблица 1.2