5.2. Спектральні оцінки часового ряду. Періодограма

Нехай спостерігається - дійсний гільбертів слабо стаціонарний процес із заданим кінцевим математичним сподіванням . Передбачається, що для даного процесу існує невідома спектральна щільність потужності і виконується ергодична теорема відносно математичного сподівання і кореляційної функції (умова сильного перемішування).

Як і у попередньому випадку оцінювання кореляційної функції, тут також спостерігається послідовність – реалізація вихідного процесу . В якості оцінки можна взяти

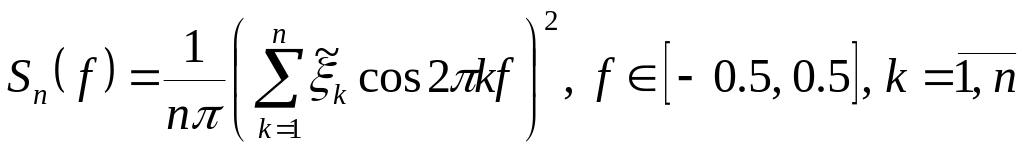, (5.12)

де .

Вираз (5.12) можна записати у вигляді

.

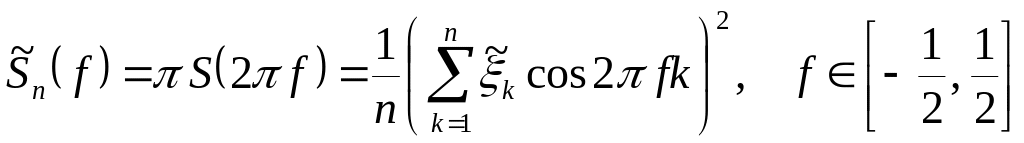Якщо відліки взяти не через одиницю часу, а з довільним постійним кроком , то останній вираз можна записати так

.

Частота - найвища частота, яку можна виявити за даними відліку через секунд – частота Найквіста – Котельнікова.

Приведений вище вигляд оцінки спектральної щільності можна пояснити таким чином. Якщо вважати значення коефіцієнтами відрізку ряду Фур'є, то є періодичною функцією від , задану на періоді , яка в цей ряд розкладена. А оскільки – оцінка спектральної щільності потужності, то наведена вище сума в оцінці (5.12) береться в квадраті умножається на .

Функцію в статистичній теорії спектральних функцій називають періодограмою. Її вперше ввів і досліджував в своїх роботах Шастер в 1898 р. і 1906 р. Якщо вихідний процес – гаусів, то періодо­грама , і , розподілена, як – хі - квадрат з двома ступінями свободи.

Приведемо без доказу математичне сподівання оцінки (5.12) при , що прямує до нескінченності

Останнє співвідношення показує, що при оцінка є асимптотично не­зміщеною для

.

Обчислення дисперсії в загальному випадку зв'язане із складними викладеннями, які спрощуються в разі аналізу гаусових процесів . Приведемо без доказу асимптотичне значення дисперсії у гаусовому випадку

5.3. Визначення законів розподілів часових рядів по даних спостережень

Варіаційний ряд. В результаті проведення спостережень над деякою випадковою величиною або часовим ергодичним рядом отримуємо ряд чисел

,

який називається вибіркою. Число називається обсягом вибірки.

Водночас зауважимо, що часовий ряд являє собою стаціонарний процес з дискретним часом. Він є ергодичним відносно одновимірної функції розподілу , тому що

,

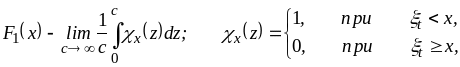тоді і тільки тоді, якщо

.

Стаціонарний ряд з незалежними значеннями - ергодичний відразу, тобто

.

Якщо всі елементи вибірки розташувати в порядку збільшення їх значень, тобто , то отримаємо варіаційний ряд .

Кожний елемент варіаційного ряду називається порядковою статистикою. Величина - різниця найбільшого та найменшого значень, називається розмахом варіювання. Деякі порядкові статистики можуть служити статистичними оцінками параметрів, що характеризують випадкову величину . Наприклад, якщо , то і - називаються вибірковими секстилями і за оцінку средньоквадратичного відхилення випадкової величини можна взяти вираз

.

За оцінку її математичного сподівання (при непарному ) беруть .

Частотою деякої події називається відношення кількості наслідків , що сприяють цій події, до загального числа наслідків . Позначимо її через .

Вибіркова функція розподілу. В попередньому підрозділі були наведені вирази для обчислення вибіркових моментів. Вони будуть істотно використані далі.

ОЗНАЧЕННЯ 5.4. Вибірковою функцією розподілу для вибірки обсягом називається функція

,

де - кількість тих порядкових статистик, значення яких менші .

На рис. 5.4 наведено типовий графік вибіркової (емпіричної) функції розподілу.

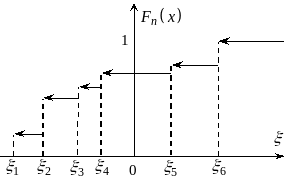
Рис. 5.4

Побудова оцінки щільності розподілу. Спостерігаються значення випадкової величини , неперервна щільність розподілу якої невідома і її потрібно оцінити по вибірці з незалежних спостережень .

Розмах варіювання розіб'ємо на інтервалів довжиною . Емпірична щільність розподілу або “гістограма” вибірки визначається на кожному інтервалі довжиною рівністю

,

де - кількість спостережень, що належать до інтервалу . Очевидно, що частота - відображає площу прямокутника, побудованого на , як на основі з висотою, що дорівнює ординаті гістограми .

Таким чином, при великому площа прямокутника за теоремою Бернуллі буде наближатися до - ймовірності потрапити значенню випадкової величини до інтервалу :

.

Тому

,

де - деяка точка на інтервалі .

Дисперсія

D D ,

тобто при та гістограма буде незсуненою і слушною оцінкою для щільності розподілу. Крім того, із ймовірністю, близькою до 1, при великому гарантується рівномірне наближення до .

Гістограма. Якщо спостережень дуже багато, - велике, то незручно будувати графік вибіркової функції розподілу . В цьому випадку користуються групуванням результатів спостережень. А саме, весь інтервал спостережень ділять на підінтервалів і будують таблицю

Інтервали			...
Частоти			...

де - границі інтервалів, - частота, що відповідає - му інтервалу, , тобто кількість значень , що потрапили в - тий інтервал, віднесене до . Переважно . Довжини інтервалів не обов'язково однакові.

Наведена вище таблиця, оформлена у вигляді графіка називається гістограмою. Інакше кажучи, гістограма - це вибіркова щільність розподілу. Будується вона так. По осі абсцис відкладаються інтервали і на кожному з них, як на основі, будується прямокутник, площа якого дорівнює частоті цього інтервалу. Приклад гістограми наведений на рис. 5.5.

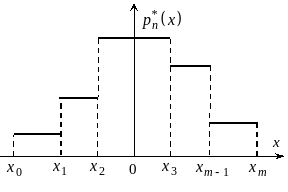
Рис. 5.5

Згладжування гістограм. Задача згладжування гістограм не має однозначного розв'язку, а тому результати її рішення істотно залежать як від використовуваної методики, так і від додаткових вимог, що використовуються в ході її рішення.

Класичним прикладом розв’язування задачі згладжування є згладжування по кривих К.Пірсона. При цьому використовується метод моментів, згідно якого спочатку обчислюються величини

.

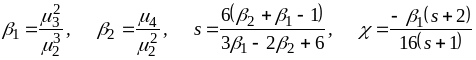Потім в залежності від значення параметра (“капа Пірсона”) вибирається тип основної згладжуючої кривої, а саме:

1-й тип при 4-й тип при 6-й тип при

Значення інших параметрів дають можливість вибирати проміжний тип кривої - згладжуючої гістограму згідно методики К.Пірсона [2,…,4]. Якість згладжування можна оцінити з допомогою статистичних критеріїв. Найбільш вживаний в цьому випадку - критерій, запропонований К.Пірсоном.