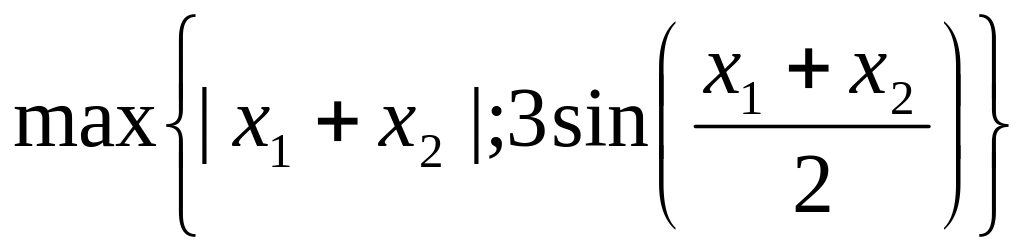Задачи и упражнения
1. Построить выпуклую функцию, определённую на [0, 1], которая не имеет производной в бесконечном числе точек.
2. Следует ли из существования конечной производной по любому направлению дифференцируемость выпуклой функции? Рассмотреть пример
.
3. Вычислить производную по направлению p R2 в точке (0, 0) функции
.
Показать, что в этой точке существует
производная по любому направлению,
однако функция не является непрерывной
в данной точке. Почему такая ситуация
невозможна для выпуклой функции?
Указание.
4. Привести пример функции, для которой субдифференциал в некоторой точке является пустым множеством.
5. Доказать, что субдифференциал f(x0) – выпуклое, замкнутое множество для любой точки x0 X.
6. Доказать, что если h(x) = αf(x), α > 0, то h(x) = α f(x) для х Х.
7. Доказать, что если f(x) = |h(x)|, x Rn, где h(x) – непрерывная функция и h(x) = 0, тогда нулевой вектор принадлежит f(a) (0 f(a)).
8. Пусть f – выпуклая функция на R, x0 int(dom f), f(x0) = {a}, где a R. Показать, что f дифференцируемая функция в точке x0 и f ’(x0) = a.
9. Пусть f: Rn
R+
- собственная функция и
f(x)
для любого x
dom
f. Доказать, что f
– выпуклая функция.
10. Найти субдифференциалы и производные по направлениям следующих функций:
а) f(x) = |x – 1| + |x + 1+, x R;
б) f(x) = max{x2, x + 2};
в) f(x) = max{2x – 3, 0.5x + 1, - x + 1};
г) f(x) = max{|x|, |x – 1|};
д) f(x) =
е) f(x) = |x1 + x2|, x R2;
ж) f(x1, x2) = |2x1 – 3x2|;
и*) f(x) =
Задания для самостоятельной работы
1. Изобразить на плоскости сумму двух множеств X1 = [x1, x2], где x1 = (4, a), x2 = (4, 3) и X2 = Conv{(-2, -1), (1, b), (3, -c)}.
-
№
варианта
a
b
c
№
варианта
a
b
c
1
2
2
1
11
4
5
3
2
2
3
1
12
4
6
3
3
2
4
1
13
4
7
3
4
2
5
1
14
4
8
3
5
2
6
1
15
1
1
0
6
3
3
2
16
1
2
0
7
3
4
2
17
1
3
0
8
3
5
2
18
1
4
0
9
3
6
2
19
1
5
0
10
3
7
2
20
4
4
3
2. Записать уравнение гипреплоскости, опорной к множеству
X1 =
в точке x0 = (a,
b, c).
-
№
варианта
a
b
c
№
варианта
a
b
c
1
-6/5
12/5
0
11
0
9/5
-4
2
-8/5
0
3
12
6/5
0
-4
3
0
9/5
4
13
8/5
-9/5
0
4
6/5
0
4
14
0
12/5
-3
5
0
12/5
3
15
8/5
0
3
6
8/5
9/5
0
16
6/5
12/5
0
7
0
-9/5
4
17
6/5
-12/5
3
8
6/5
-12/5
0
18
-6/5
0
4
9
8/5
0
-3
19
-8/5
-9/5
0
10
0
-9/5
-4
20
0
-12/5
-3
3. Найти проекцию точки х0 = (a, b, c) на множество Х = {x R3 : x3 x12 + x22}.
-
№
варианта
a
b
c
№
варианта
a
b
c
1
5/4
5/16
15/16
11
9/8
27/32
3/2
2
4/3
2/3
13/12
12
5/4
5/4
15/8
3
5/3
5/9
7/9
13
9/8
9/32
1
4
5/4
15/16
23/16
14
4/3
4/9
17/18
5
5/3
10/9
10/9
15
5/3
5/6
11/12
6
3/2
3/2
7/4
16
11/9
22/27
4/3
7
3/2
3/8
13/16
17
7/5
14/25
24/25
8
5/4
5/8
9/8
18
3/2
3/4
1
9
10/9
10/27
19/18
19
4/3
8/9
23/18
10
13/9
26/27
11/9
20
11/9
11/27
1
4. Записать уравнение гиперплоскости, разделяющей множества
X1 = {x
R2:
x1x2
1,
x1 > 0} и X2
= {x
R2:
x2
}.
-
№
варианта
a
b
c
№
варианта
a
b
c
1
1/9
2/3
8/3
11
1/4
1/2
9/2
2
4
1
9
12
25
2
18
3
1/4
1
9/4
13
9/4
5
5/4
4
25
12
3
14
9
8
2
5
1/9
16/3
1/3
15
25
3
12
6
25
18
2
16
1/4
9/4
1
7
25
9
4
17
1/9
1/3
16/3
8
1/4
9/2
1/2
18
25
4
9
9
1/9
8/3
2/3
19
9/4
5/4
5
10
9
2
8
20
1
4
1
5. Доказать, что функция на заданном множестве выпукла
№ вари- анта |
Функция |
Множество |
1 |
|
x R2 |
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
6. Проверить, является ли функция f выпуклой (вогнутой) на заданном множестве Х, или указать такие точки из Х, в окрестности которых f не является ни выпуклой, ни вогнутой.
-
№
варианта
Функция
Множество
1
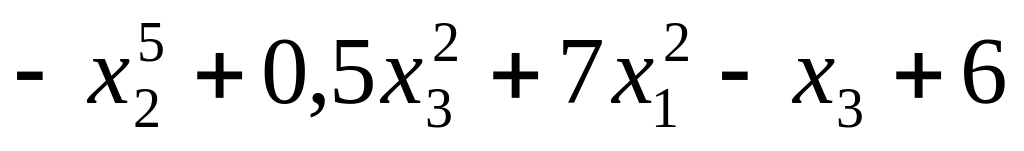
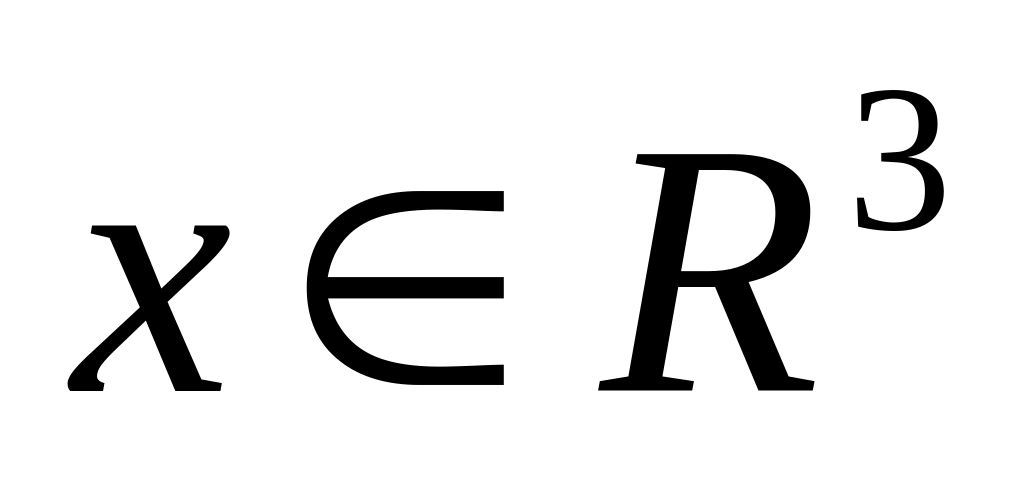
2
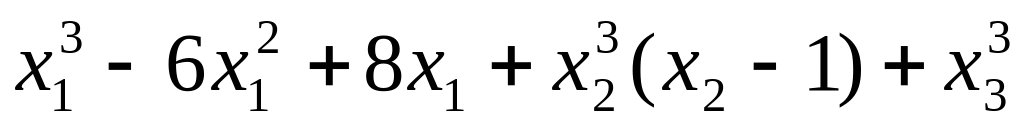
3
4
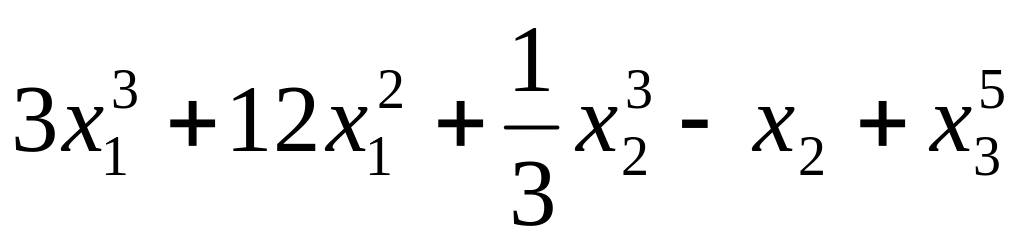
5
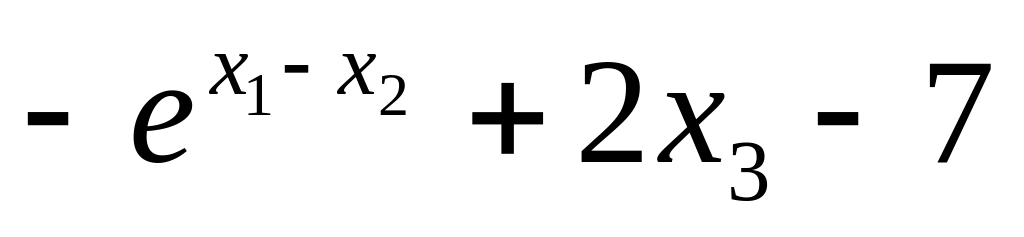
6
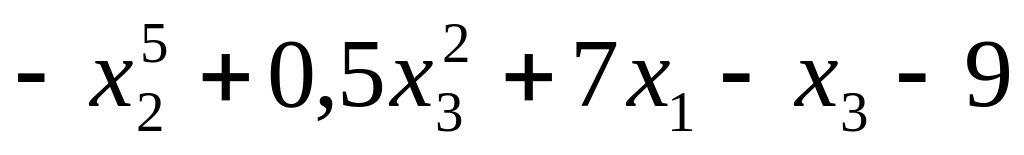
7
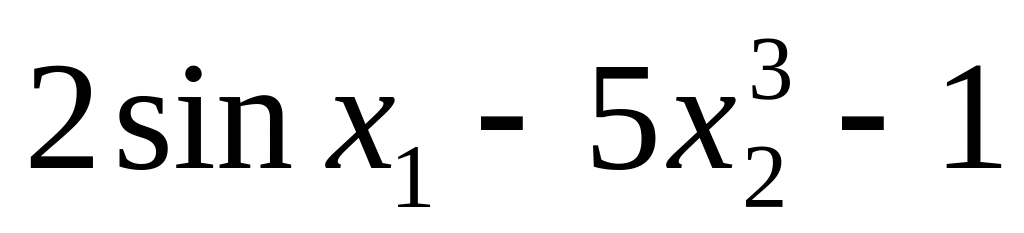
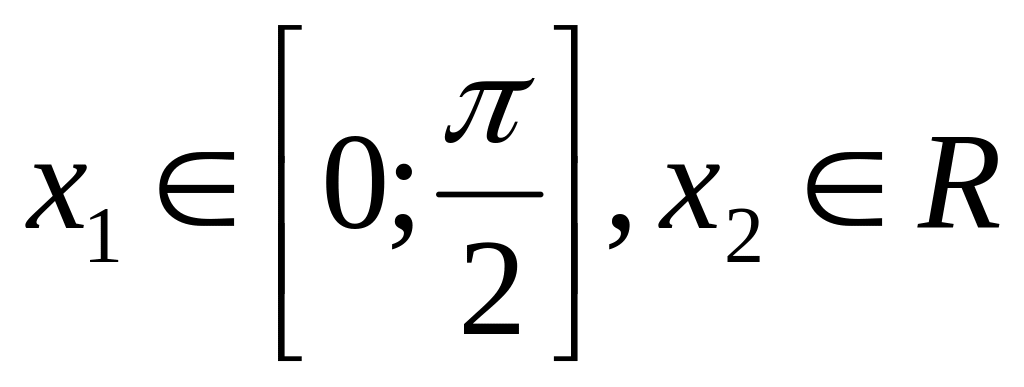
8
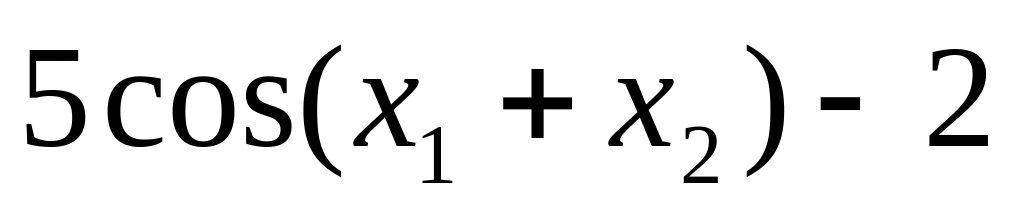
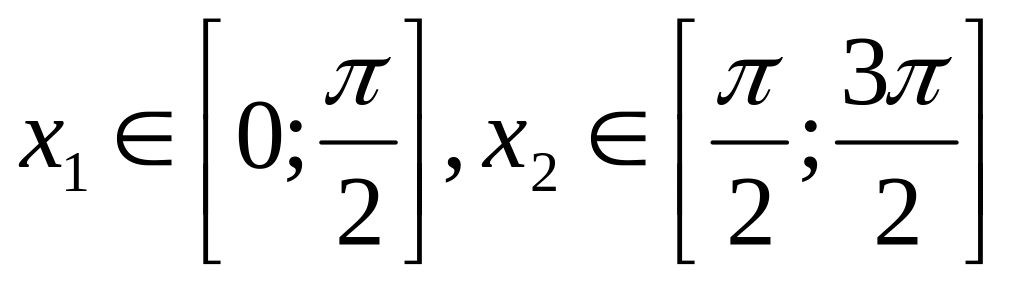
9
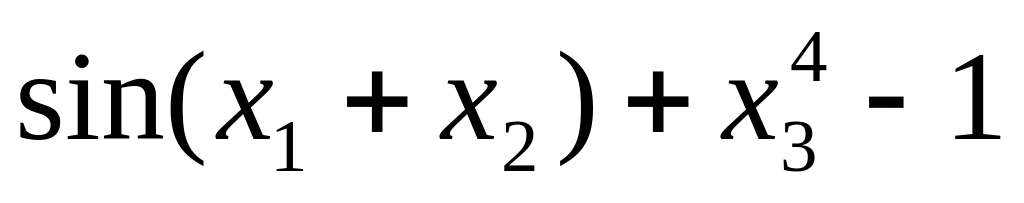
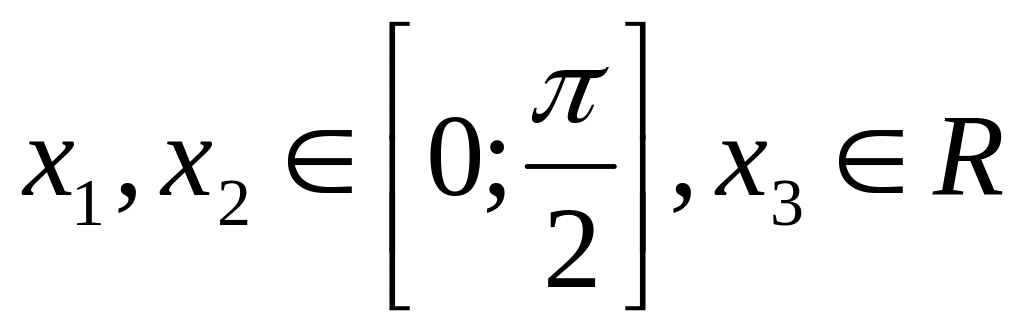
10
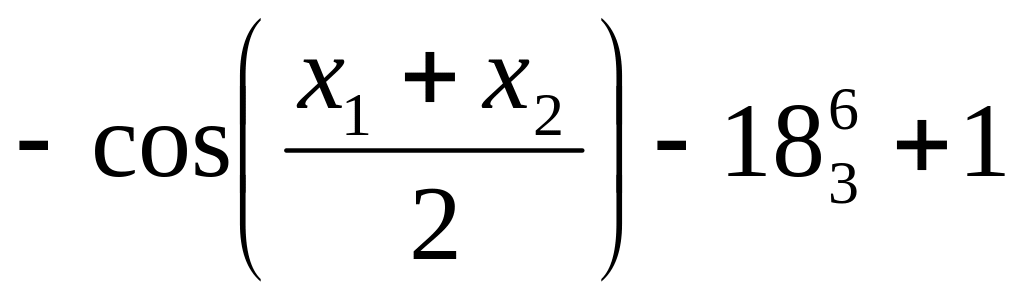
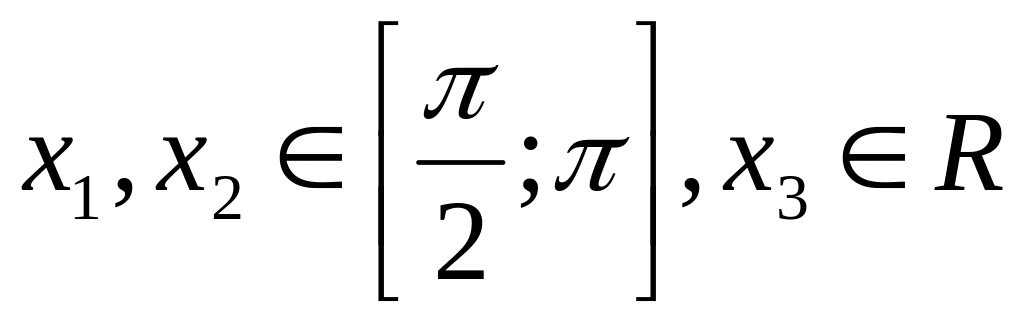
11
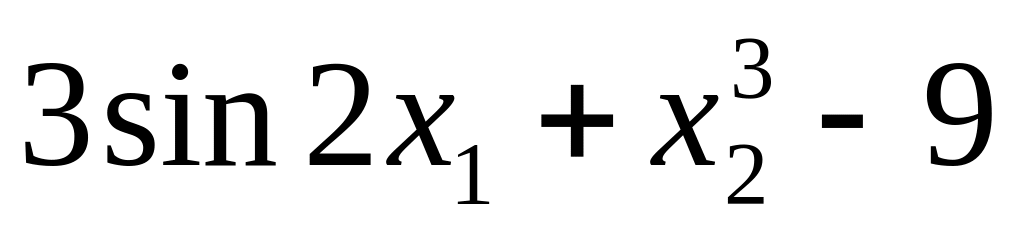
12
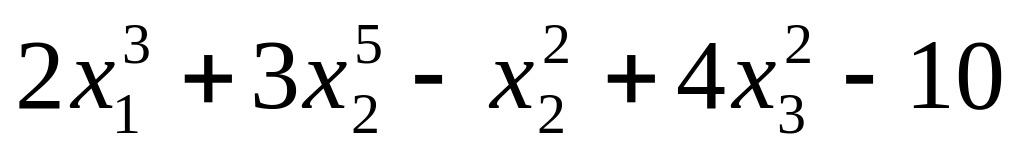
13
14
15
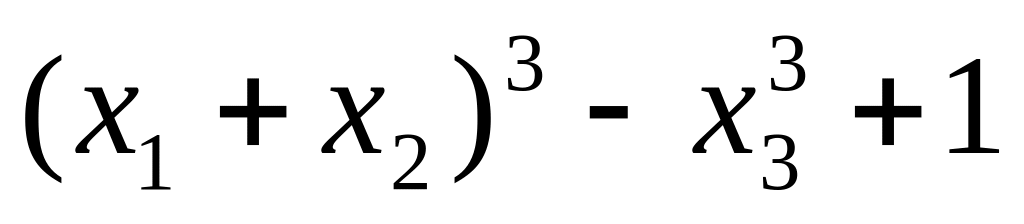
16
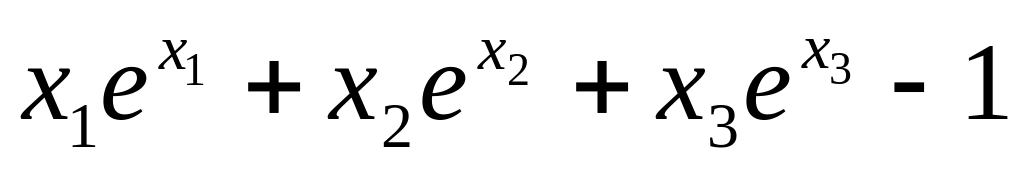
17
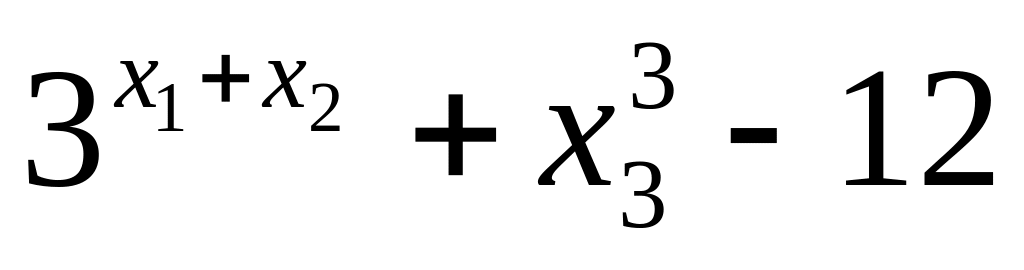
18
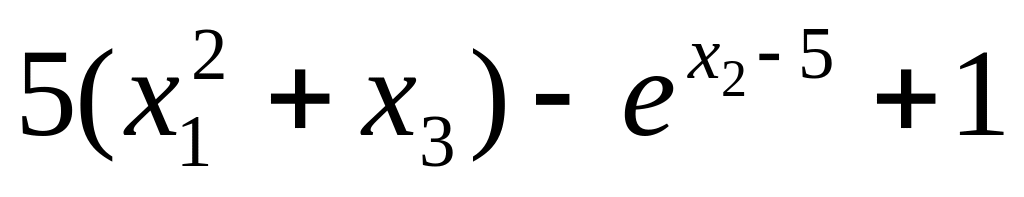
19
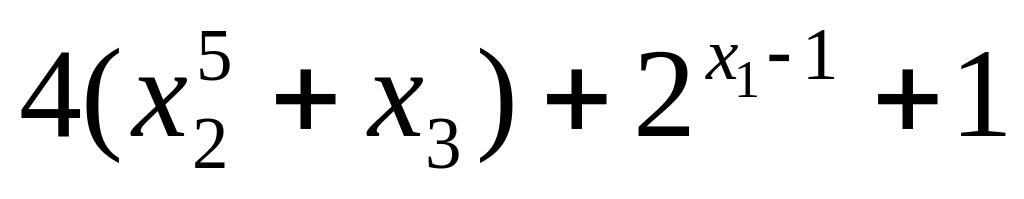
20
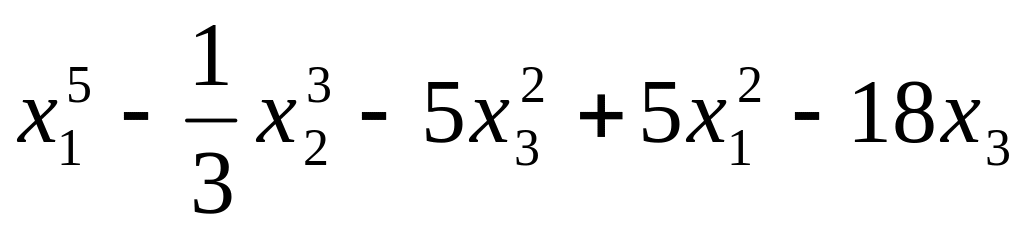
7. Вычислить субдифференциал функции f(x), определённой на всём пространстве, и производные по всем направлениям координатных осей пространства.
-
№ варианта
Функция
1
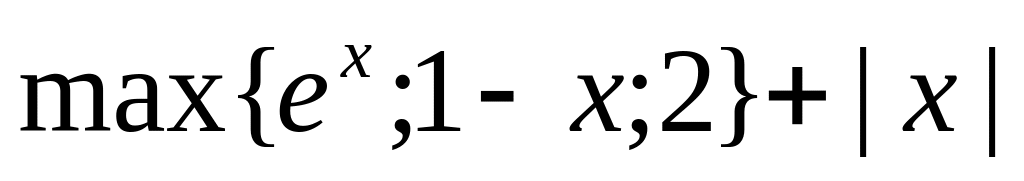
2
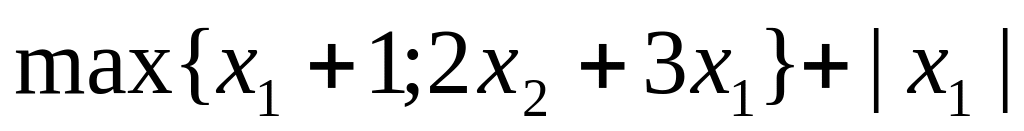
3
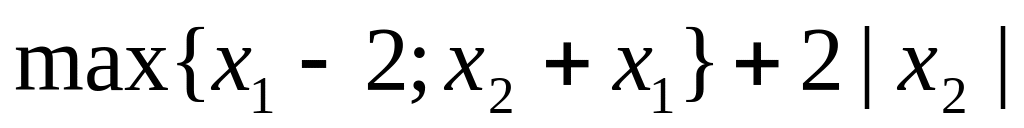
4
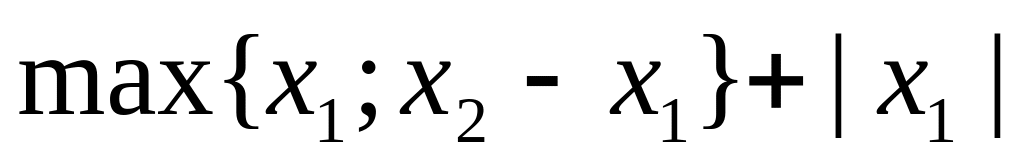
5
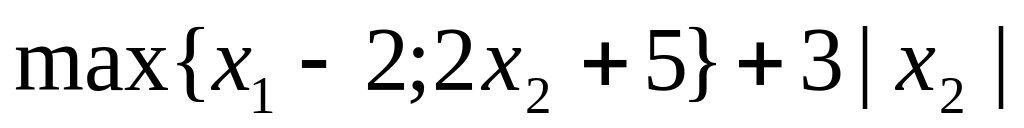
6
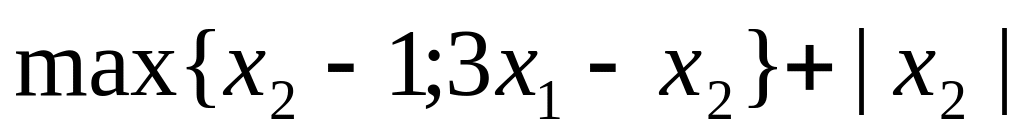
7
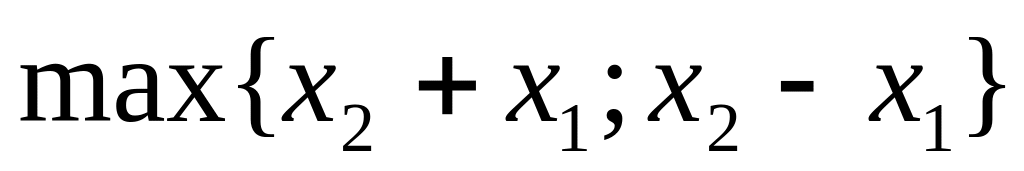
8
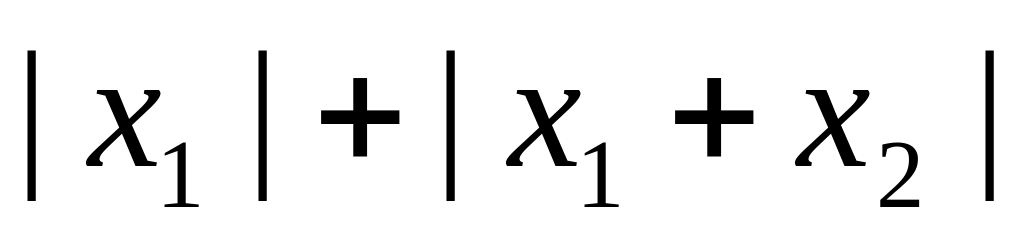
9
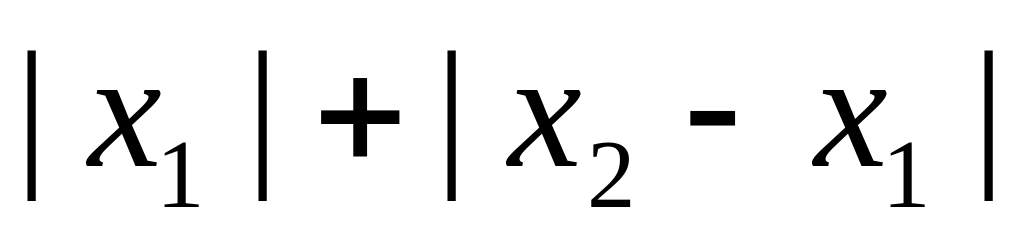
10
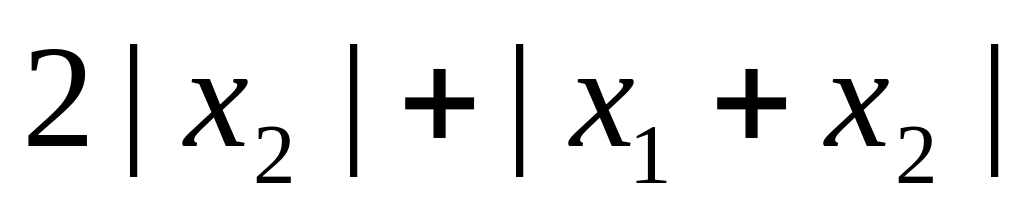
11
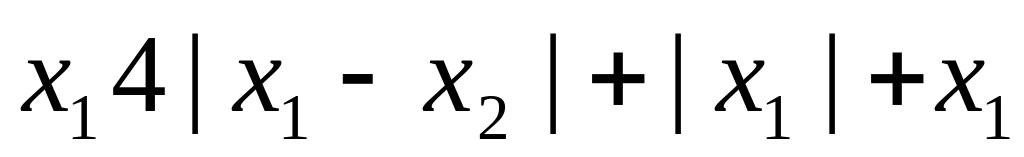
12
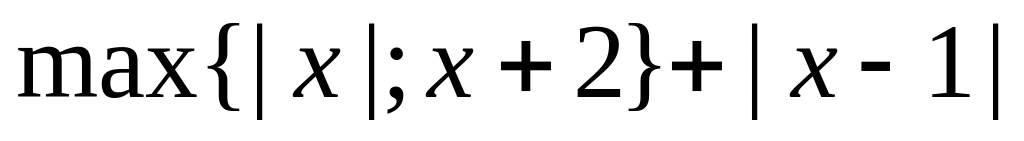
13
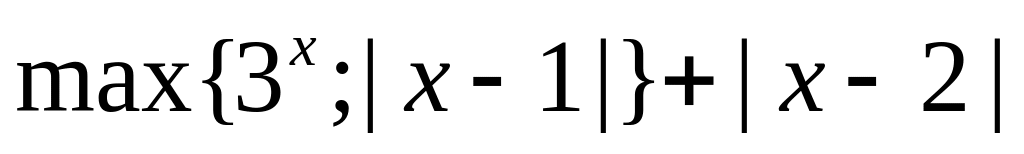
14
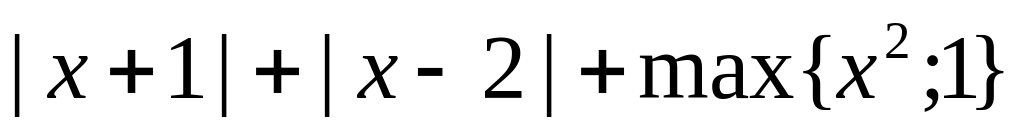
15
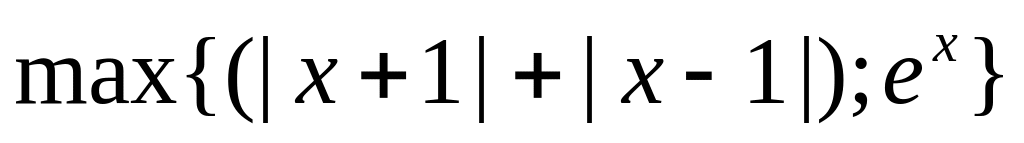
16
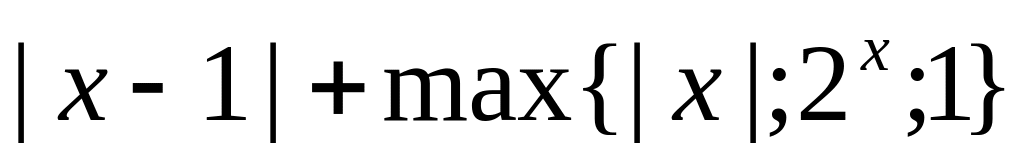
17
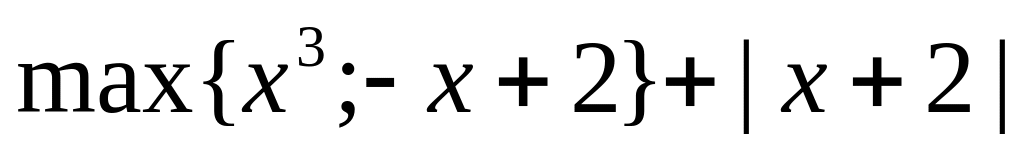
18
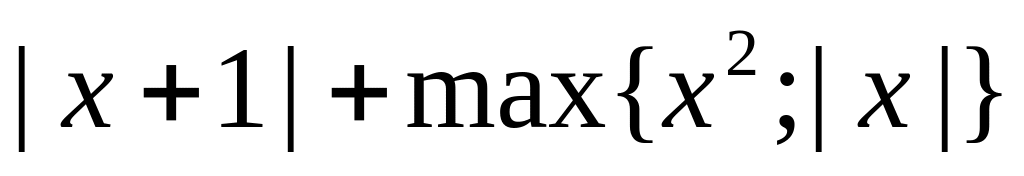
19
20
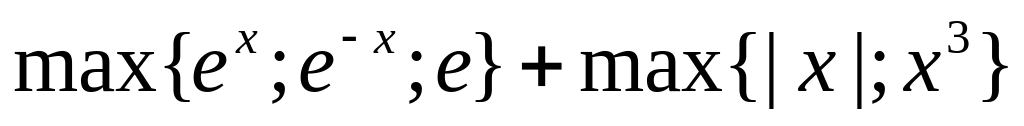
Задание № 1
1. Доказать 1, 2, 3, 4, 5 свойства выпуклых множеств, сформулированные на стр. 4-5.
2. Решить задачи 2-9, 12, 13, на стр. 8, 10.
3. Доказать 1-4 свойства выпуклых функций, сформулированные на стр. 12, 13.
4. Решить задачи 1-13, 16, 17(а), 21(б), 24 на стр. 14-18.
5. Доказать 1-4 свойства субдифференциала, сформулированные на стр. 20.
6. Решить задачи 1-3, 6, 7, 10 на стр. 24, 25.
7. Выполнить 1 вариант заданий для самостоятельной работы на стр. 26-31.
Задание № 2
Выполнить упражнения и решить задачи из методички «Милизация функций многих переменных».
Задание № 3
По методичке «Метод Ньютона, как обобщённый градиентный метод».
1. Выполнить упражнения из методички.
2. Решить задачи 1, 2, 4, 5, 6, 7-14 на стр. 21-23.
Задание № 4
Решить задачи 6-12 из методички «Принцип Лагранжа в гладких конечномерных задачах».
Задание № 5
По книге Галеева Э. М. и Тихомирова В. М. «Краткий курс теории экстремальных задач».
1. Изучить теоретический материал $$ 4, 5, 6 стр. 68-104.
2. Найти процессы, удовлетворяющие необходимым условиям минимума в задачах 86, 88-90, 92, 97 стр. 173.
114, 121, 123, 128, стр. 175.
147, 150, 152, 154, 156, 158, стр. 177.
194, 196, 198, стр. 180.
220, 224, 226, стр. 182.
239, 243, 247, стр. 184.
255, 256, 257, стр. 185.