
3. Производные по направлениям и субдифференциалы
Выпуклые функции в общем случае могут быть недифференцируемы в обычном смысле (например, f(x) = |x| недифференцируема в точке х = 0).
Определение. Производной по
направлению p(p
Rn,
p
0)
функции f в точке х
называется
![]()
![]() и обозначается f ’(x,
p) или
и обозначается f ’(x,
p) или
![]() (х).
(х).
Отметим, что если f(x) дифференцируема в точке х, то f ’(x, p) = (f ’(x),p), где
f ’(x) =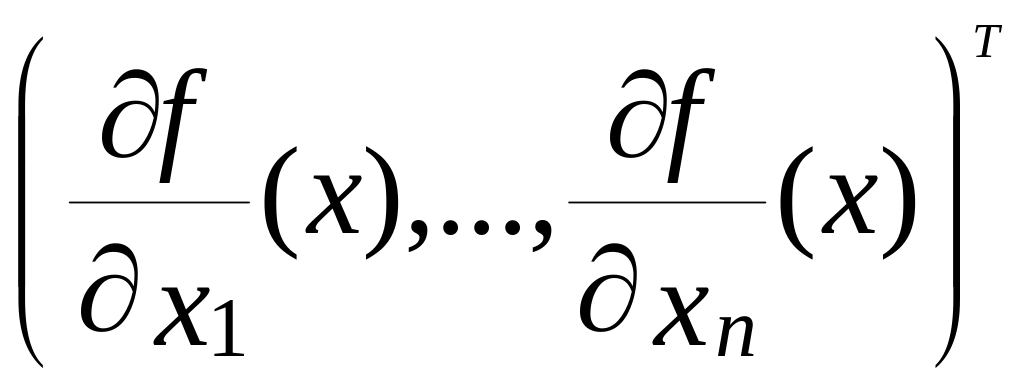 - градиент функции f в
точке х.
- градиент функции f в
точке х.
Теорема Радемахера. Всякая выпуклая функция является дифференцируемой почти всюду (за исключением множества лебеговой меры нуль) на открытом множестве Х dom f.
Теорема. Пусть f(x) – выпуклая функция на Rn. Тогда для любой точки х int(dom f) существует и конечна производная функции f по любому направлению pRn.
Для выпуклых функций можно определить понятие субградиента, которое заменяет обычное понятие градиента гладкой функции в задачах на экстремум.
Определение. Вектор g называется субградиентом функции f в точке х0 dom f, если
f(x) – f(x0) (g, x – x0) для любых х Rn.
Множество всех субградиентов функции f в точке х0 называется субдифференциалом функции f и обозначается f(x0).
Замечание. В определении субградиента не требуется выпуклости функции и можно вычислить субградиент в заданной точке и для произвольной функции. Однако для выпуклой функции, определённой на открытом выпуклом множестве, всегда существует хотя бы один субградиент в любой точке множества, т.е. её субдифференциал является непустым множеством. Для произвольной функции это не так.
Геометрический смысл понятия субдифференциала
Можно показать, что если f(x) выпуклая функция, то
1) вектор g![]() f(x0)
является внешней нормалью
опорной гипреплоскости к множеству
уравня M(f)
функции f в точке х0,
где M(f) =
{x
Rn|
f(x)
f(x0)};
f(x0)
является внешней нормалью
опорной гипреплоскости к множеству
уравня M(f)
функции f в точке х0,
где M(f) =
{x
Rn|
f(x)
f(x0)};
2) вектор (g, - 1)Rn+1, где g f(x0), является внешней нормалью опорной гиперплоскости, проведённой к надграфику функции f в точке (x0, f(x0)) (в частности, если x R, то g есть тангенс угла наклона опорной прямой, проведённой к надграфику функции f);
3) для функции f: R R f(x) = [f ’(x – 0), f ’(x + 0)].
Свойства субдифференциала выпуклой функции
Пусть f(x) – выпуклая функция, определённая на открытом выпуклом множестве Х dom f. Тогда справедливы следующие утверждения.
1. Субдифференциал f(x0) – непустое выпуклое, замкнутое и ограниченное множество для любой точки х0 Х.
2. Если f(x) – дифференцируемая функция в точке х0 Х, то
f(x0) = {f ’(x0)}.
3. Пусть h(x) = αf(x), α > 0, тогда
h(x) = αf(x) для x X
4. Пусть f(x) = f1(x) + f2(x), где f1(x) и f2(x) – выпуклые на Х функции, тогда
f(x) = f1(x) + f2(x) для х Х.
5. Пусть функции f1,
f2, … ,fm
– выпуклые функции, определённые на Х,
и f(x) =
![]() fi(x).
Тогда
fi(x).
Тогда
f(x)
= conv![]() для
х
Х,
для
х
Х,
где I(x) = {i = : fi(x) = f(x)}.
6.Производная функции f в произвольной точке по любому направлению p Rn, p 0 существует и
f ’(x, p)
=
![]() (g, p).
(g, p).
Замечание. Требование открытости множества Х существенно. Если Х – произвольное выпуклое множество, то в его граничных точках свойства 1 – 6 будут выполняться только при некоторых дополнительных предположениях.
В общем случае вычисление субдифференциала f(x) задача непростая. Один из инструментов решения этой задачи даёт теорема Кларка.
Теорема Кларка. Пусть x0
int
dom f, f(x)
– выпуклая функция на Rn,
Q – множество точек
пространства Rn,
в которых функция f(x)
недифференцируема, {xk}
– произвольная последовательность,
сходящаяся к x0(xk
Q
для любого k), такая, что
последовательность
![]() сходится. Тогда субдифференциал функции
f(x) в точке
x0 совпадает с
выпуклой комбинацией всех пределов
последовательностей
сходится. Тогда субдифференциал функции
f(x) в точке
x0 совпадает с
выпуклой комбинацией всех пределов
последовательностей
![]() для всевозможных последовательностей
{xk},
т.е.
для всевозможных последовательностей
{xk},
т.е.
f(x0)
= Conv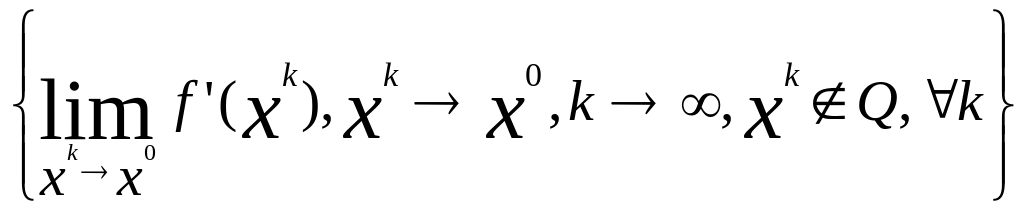 .
.
Примеры
1. Пусть f(x) = |x|. Требуется вычислить f(x). Если х > 0, то f(x) = x, f ’(x) = 1, следовательно,
f(x) = Conv{1} = {1}. Аналогично для x < 0 f(x) = Conv{-1} = {-1}. Пусть х = 0. Заметим, что это единственная точка, в которой функция f(x) недифференцируема. Тогда
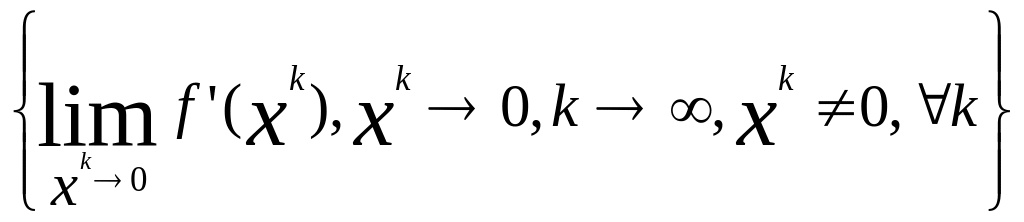 = {-1, +1},
= {-1, +1},
f(0) = Conv{-1, +1} = [-1, 1].
2. Пусть f(x1, x2) = |x1| + |x2|. Требуется вычислить f(x).
З аметим,
что f(x1,
x2) =
аметим,
что f(x1,
x2) =
Функция f(x1,
x2) дифференцируема
в любой точке пространства, кроме точек,
для которых выполнено одно из условий:
|x1| = 0 или |x2|
= 0, т.е. Q = {x
R2:
x1 = 0}![]() {x
R2:
x2 = 0}.
{x
R2:
x2 = 0}.
Пусть x
Q,
тогда f ’(x1,
x2) =
![]() ,
если x1 > 0, x2
> 0;
,
если x1 > 0, x2
> 0;
f
’(x1, x2)
=
![]() ,
если x1 > 0, x2
< 0;
,
если x1 > 0, x2
< 0;
f ’(x1,
x2) =
![]() ,
если x1 < 0, x2
> 0;
,
если x1 < 0, x2
> 0;
f ’(x1,
x2) =
![]() ,
если x1 < 0, x2
< 0.
,
если x1 < 0, x2
< 0.
На Рис. 13 представлены области, в которых функция дифференцируема и значения градиентов одинаковы.
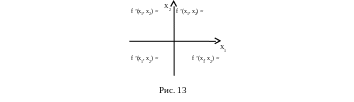 Для точек
х0
Q
субдифференциал состоит из единственного
элемента, совпадающего с градиентом
функции в этой точке.
Для точек
х0
Q
субдифференциал состоит из единственного
элемента, совпадающего с градиентом
функции в этой точке.
Пусть х0 Q, причём х0 лежит на оси Ох1 и х10 > 0. Тогда
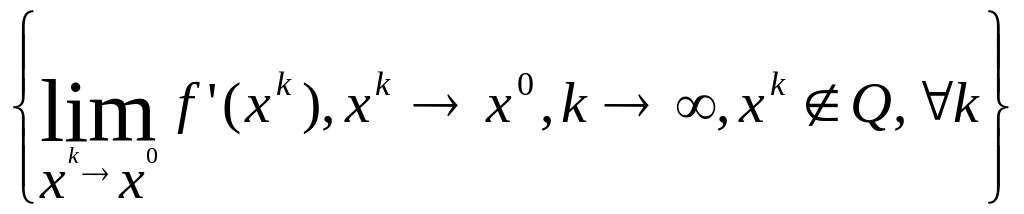 =
=![]() поэтому
поэтому
![]()
Аналогично вычисляется субдифференциал для других точек множества Q. Таким образом,
![]()
Заметим, что некоторые свойства субдифференциалов, приведённые выше, легко получить как следствие из теоремы Кларка.
