Задачи и упражнения

1. Пусть х⁰ Rⁿ , r R, r > 0. Является ли выпуклым шар радиуса r без центра

S(x⁰,r) = {x Rⁿ : |x-x⁰|| r}\{x⁰}?

2. Приведите пример односвязного невыпуклого множества, которое в результате удаления из него нескольких точек становится выпуклым.

3. Показать, что множество Х = {x Rⁿ : Ax = b, x 0} выпукло.

4. Являются ли выпуклым множество Х Rⁿ, если для любых x и v из X точка (х + +v) X?

5. Пусть x,v Rⁿ и x v . Проверить выпуклость множества Y = {y Rⁿ : y = (1-α)x + αv, α R}.

Замечание: Y – прямая, проходящая через точки x и v.

6. Верно ли, что если - выпуклое множество, то Х – выпукло? Верно ли, что если int X– выпуклое множество, то Х – выпукло?

7. На плоскости даны множества Х₁ и Х₂ (рис. 9 – 11), построить множества Х₁ + Х₂ и Х₁ – Х₂.

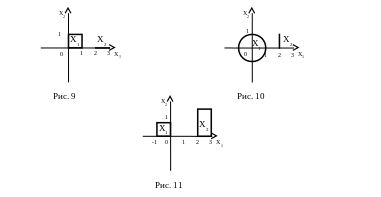
8. Пусть Х = Х₁ – Х₂. Следует ли отсюда, что Х₁ = Х + Х₂? Рассмотреть пример множеств, заданных на рис. 12.

9. Построить выпуклую и замкнутую выпуклую оболочку множества Х :

1) Х = {x R² : x₁² = x₂};

2) X = epi f, f(x) = |x|, x R;

3) X = epi f, f(x) =

4) X = epi f, f(x) = , x R ;

5) X = epi f, f(x) =

10. Пусть Х = {x Rⁿ : a_i x_i b_i, i = }, y Rⁿ. Построить проекцию точки y на X.

11. Пусть Х = {x Rⁿ : ||x – a|| R}, a Rⁿ. Построить проекцию точки y Rⁿ на X.

12. Построить опорную гиперплоскость к множеству Х в точке х⁰ :

1) Х = {xR3 : x₁² – 2x₁x₂ + 10x₂² + 6x₂x₃ + x₃² 25},x⁰ = (4,1,1);

2) X = {x R² : e^x1 x₂, x₂ 1}, x⁰ = (0,1).

13. Построить разделяющую гиперплоскость для выпуклых множеств Х₁ и Х₂ :

X₁ = {x R² : x₂(x₁ - 1) 3, x₁<1},

X₂ = {x R² : (x₂ + 4)(x₁ + 2) 3, x₁> - 2}.

14*. Доказать, что если Х – выпуклое множество с непустой внутренностью, то луч, проведённый из любой внутренней точки множества Х, пересекает границу Х не более, чем в одной точке.

2.Выпуклые функции

Будем рассматривать заданные на пространстве Rⁿ функции f(x), значения которых принадлежат расширенной действительной оси . Таким образом, допускается, что функции принимают значения - и + . Обозначим R₊ = R .

Определение. Функция f, называется выпуклой, если её надграфик epi f – выпуклое множество.

Обозначим dom f = {x : f(x)<+ }. dom f называется эффективной областью функции f.

Определение. Функцию f будем называть собственной, если f(x)> - для любых x Rⁿ и dom f 0.

Пример. Функции f(x) = х² и f(x) = являются собственными, а функция

f(x) = . не является собственной.

Теорема. Собственная функция f, является выпуклой, если и только если

f(αx + (1-α)y) αf(x) + (1-α)f(y) (1)

для любых х и у и любого α [0,1] .

Замечание. Для собственных функций выполнение неравенства (1) можно рассматривать как определение выпуклых функций.

Далее мы будем рассматривать только собственные функции.

Определение. Функция f называется строго выпуклой, если

f(αx + (1 - α)y)<αf(x) + (1 - α)f(y) (2)

для любых х и у и любого α (0,1).

Определение. Функция f называется вогнутой, если функция –f является выпуклой.

Определение. Функция f называется сильно выпуклой с константой >0, если

f(αx + (1 – α)y) αf(x) + (1 – α)f(y) – α(1 – α)||x-y||² (3)

для любых х, у и любого α [0,1].

Замечание. Пусть Х – выпуклое множество, Х Rⁿ. Тогда функция называется выпуклой на множестве Х, если выполняется неравенство (1) для любых х, у Х. Аналогично определяется строго выпуклая и сильно выпуклая функция на множестве Х.

Примеры.

1. Функции f(x) = 2x, f(x) = x², f(x) = e^x, x R являются выпуклыми.

2. f(x) = x² и f(x) = e^x – строго выпуклые функции; f(x) = 2x не является строго выпуклой функцией.

3. f(x) = x² – сильно выпуклая функция. Заметим, что f(x) = e^x не является сильно выпуклой.