Министерство общего и профессионального образования

Российской Федерации

Челябинский государственный университет

Элементы выпуклого анализа

Методические указания к практическим занятиям

По курсу «Методы оптимизации»

Челябинск 1998

1. Выпуклые множества

Будем рассматривать векторы x, принадлежащие n-мерному пространству Rⁿ . Заметим, что введенные ниже понятия можно распространить на произвольное линейное нормированное пространство Е. Большая часть приведенных ниже теорем при некоторых дополнительных предположениях будут также справедливы в пространстве Е. Однако в целях простоты и наглядности изложения ограничимся случаем пространства Rⁿ .

Определение. Множество X Rⁿ называется выпуклым, если для любых точек x X и y Y и любого числа [0,1] точка z = x +(1- )y также принадлежит множеству X.

Таким образом, по определению любое выпуклое множество вместе с каждыми своими двумя точками x и y содержит весь отрезок, их соединяющий.

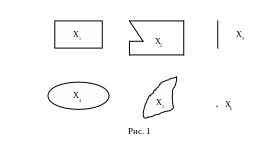
Упражнение. Какие из представленных на рис. 1 множеств являются выпуклыми?

Определение. Будем говорить, что точка x является выпуклой линейной комбинацией точек x₁,x₂,…,x_m, если существуют числа α₁,α₂,…,α_m такие, что

α_i 0,i = , α₁+α₂+…+α_m=1 и x=α₁x₁+α₂x₂+…+α_mx_m.

Определение. Пересечение всех выпуклых множеств, содержащих данное множество X, называется выпуклой оболочкой множества X и обозначается Conv X.

Пусть в Rⁿ определенно (x,y) – скалярное произведение векторов x и y, ||x|| = - норма вектора x.

Определение. Точка x называется внутренней точкой множества X, если существует >0 такое, что множество O_ε(x)={y Rⁿ: ||x-y|| ε} содержится в X.

Определение. Множество внутренних точек множества X называется внутренностью множества X и обозначается int X.

Определение. Совокупность всех предельных точек множества X называется замыканием X и обозначается .

Определение. Замыкание выпуклой оболочки множества X называется замкнутой выпуклой оболочкой X и обозначается .

Определение. Точка x называется граничной точкой множества X, если любая её окрестность содержит как точки, принадлежащие X, так и точки не принадлежащие X. Множество всех граничных точек множества X называется его границей и обозначается X.

Свойства выпуклых множеств.

1. Пересечение произвольного числа выпуклых множеств выпукло, т.е. если X_i – выпуклое множество, i I, где I – произвольный набор индексов, то X = X_i – выпукло.

2. Если множества X₁ и X₂ – выпуклы, а₁ и а₂ – произвольные вещественные числа, то множество X = а₁X₁ + а₂X₂ – выпукло, где

а₁X₁ + а₂X₂ = {x Rⁿ: x = a₁x₁+a₂x₂, x₁ X₁, x₂ X₂}.

3. Если X – выпуклое множество и точки х₁,х₂,…,х_m принадлежат Х, то Х содержит все их выпуклые линейные комбинации.

4. Выпуклая оболочка произвольного множества Х совпадает с множеством всех выпуклых комбинаций точек из Х.

Замечание. Из свойств 3 и 4 следует критерий выпуклости: множество Х выпукло в том и только в том случае, если оно содержит все выпуклые комбинации своих точек.

4. Пусть Х – выпуклое множество, тогда и int X – выпуклые множества.

Важную роль в теории экстремальных задач играют теоремы отделимости.

Теорема о разделяющей гиперплоскости. Пусть Х – замкнутое, выпуклое множество, а – точка в пространстве Rⁿ, а Х. Тогда существует гиперплоскость с нормалью р 0 такая, что

(р,а)>с и (р,х) с для х Х.

Геометрически существование разделяющей гиперплоскости можно продемонстрировать следующим образом.

Замечание. Если не выполнены условия теоремы, то разделяющую гиперплоскость провести можно не всегда (см. рис. 3)

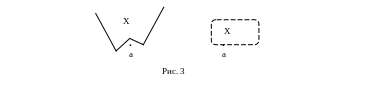
Определение. Гиперплоскость (р,х) = с называется опорной к множеству Х в точке х₀ Х, если для х Х выполняются соотношения

(р,х) с и (р,х₀) = с.

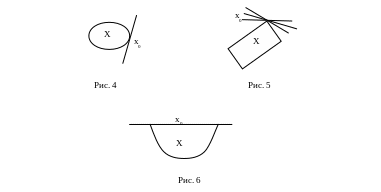
На рис. 4 – 6 приведены примеры взаимного расположения выпуклого множества Х и гиперплоскостей, опорных к Х в точке х₀.

Теорема об опорной гиперплоскости. В любой граничной точке х₀ к выпуклому замкнутому множеству Х можно построить опорную гиперплоскость.

Следует заметить, что для невыпуклых множеств это неверно: не через всякую граничную точку можно провести опорную гиперплоскость; так, на рис. 7 изображено множество Х, для которого через точку х₀ нельзя провести опорную гиперплоскость.

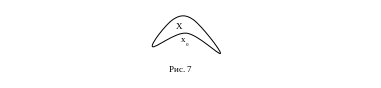Теорема отделимости. Если Х₁ и Х₂ – выпуклые непересекающиеся множества, то существует вектор р Rⁿ, р 0 такой, что (р,х₁) (р,х₂) для любых х₁ Х и х₂ Х₂.

Определение. Пусть f : Rⁿ R. Множество пар y R и x Rⁿ таких, что f(x) y называется надграфиком функции f и обозначается epi f.

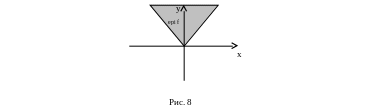
Пример. На рис. 8 изображён надграфик функции f(x) = |x|, область epi f находится над графиком y = |x|.

Определение. Проекцией точки а Rⁿ на множество Х Rⁿ называется точка р Х такая, что

||p-a|| ||x-a|| для любых х Х и обозначается Р_х(а).

Теорема. Пусть Х – выпуклое, замкнутое множество, точка а Rⁿ. Тогда проекция Р_х(а) существует и единственна.