- •Матрицы. Системы линейных уравнений
- •1. Матрицы
- •1.1. Основные понятия
- •1.2. Действия с матрицами
- •1.3. Задачи
- •2. Определители
- •2.1. Основные понятия
- •2.2. Свойства определителя
- •2.3. Алгебраические дополнения. Миноры. Формулы разложения определителя по столбцу или строке
- •2.4. Вычисление определителей
- •2.5. Задачи
- •3. Обратная матрица
- •3.1. Задачи
- •4. Ранг матрицы
- •4.1. Основные понятия
- •4.2. Вычисление ранга матрицы
- •4.3. Задачи
- •5. Системы линейных уравнений
- •5.1. Основные определения
- •5.2. Квадратные системы. Формулы Крамера
- •5.3. Метод Гаусса
- •5.4. Задачи
- •6. Однородные линейные системы
- •6.1. Общее решение однородной системы
- •6.2. Задачи
- •7. Неоднородные системы
- •7.1. Общее решение неоднородной системы
- •7.2. Задачи
- •Литература
5.3. Метод Гаусса
Идея метода Гаусса состоит в том, что путем последовательного исключения неизвестных система уравнений превращается в ступенчатую (в частности, треугольную) эквивалентную систему уравнений.
Ступенчатой системой называется система вида
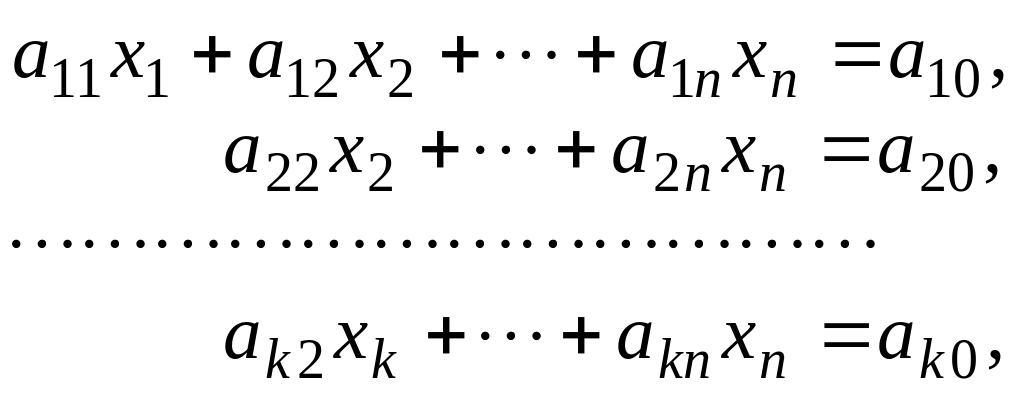
где
и
![]() .
При
.
При
![]() получаем треугольную систему. Очевидно,
что треугольная система имеет единственное
решение. Если
получаем треугольную систему. Очевидно,
что треугольная система имеет единственное
решение. Если
![]() ,
то система уравнений является
неопределенной. При этом
первых переменных можно принять за
главные, а остальные за свободные
неизвестные.
,
то система уравнений является
неопределенной. При этом
первых переменных можно принять за
главные, а остальные за свободные
неизвестные.
Для приведения системы уравнений к ступенчатому виду используются следующие преобразования, переводящие систему в эквивалентную:
1) перестановка любых двух уравнений,
2) умножение обеих частей уравнений на одно и тоже число,
3) прибавление к обеим частям уравнения соответствующих частей другого уравнения.
В результате таких преобразований получается или совместная ступенчатая система, эквивалентная исходной, или несовместная ступенчатая система. Несовместной будет система, в которой одно из уравнений имеет в правой части отличный от нуля свободный член, а коэффициенты в левой части равны нулю. В этом случае исходная система также несовместна.
При решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему, а ее расширенную матрицу, выполняя все преобразования над ее строками.
Пример. Решить методом Гаусса систему уравнений
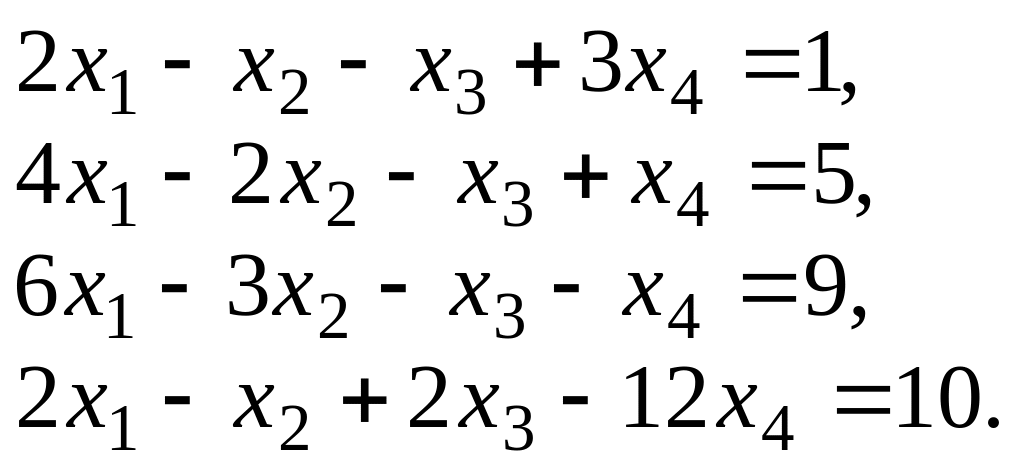
Выпишем расширенную матрицу системы. Умножая первую строку матрицы соответственно на 2, 3, 1, вычтем ее из второй, третьей и четвертой строк:
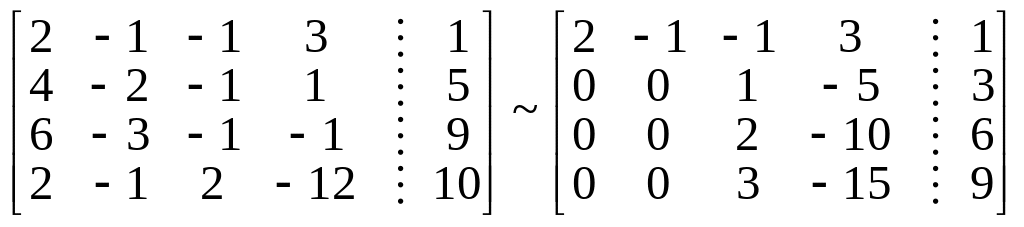 .
.
Умножим вторую строку на 2 и 3 и вычтем ее из третьей и четвертой. В итоге получим матрицу
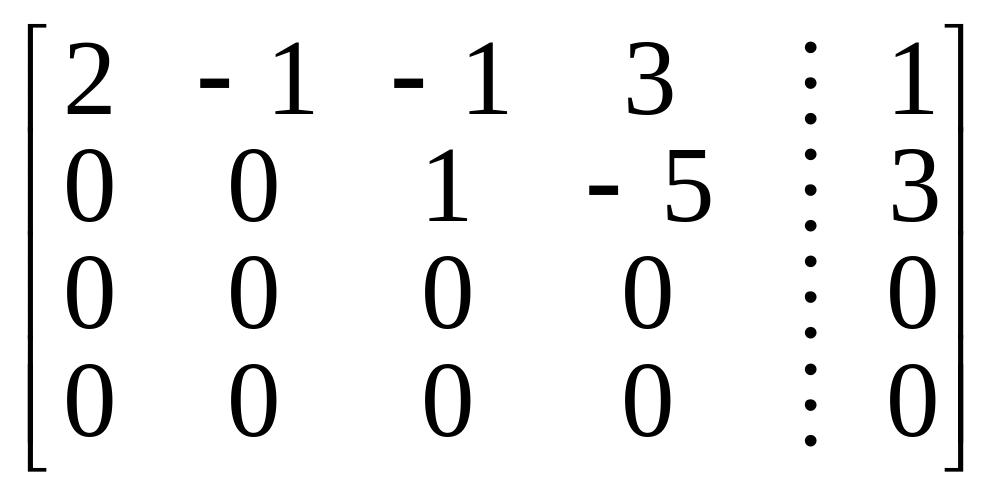 .
.
Таким образом, эквивалентная ступенчатая система имеет вид
![]()
За главные неизвестные
можно принять
![]() и
и
![]() ,
а за свободные
,
а за свободные
![]() .
Выражая главные через свободные, получим
.
Выражая главные через свободные, получим
![]()
Поэтому общее решение нашей системы есть вектор – столбец

где свободные переменные могут принимать любые значения.
5.4. Задачи
Решить системы уравнений с помощью правила Крамера.
1.
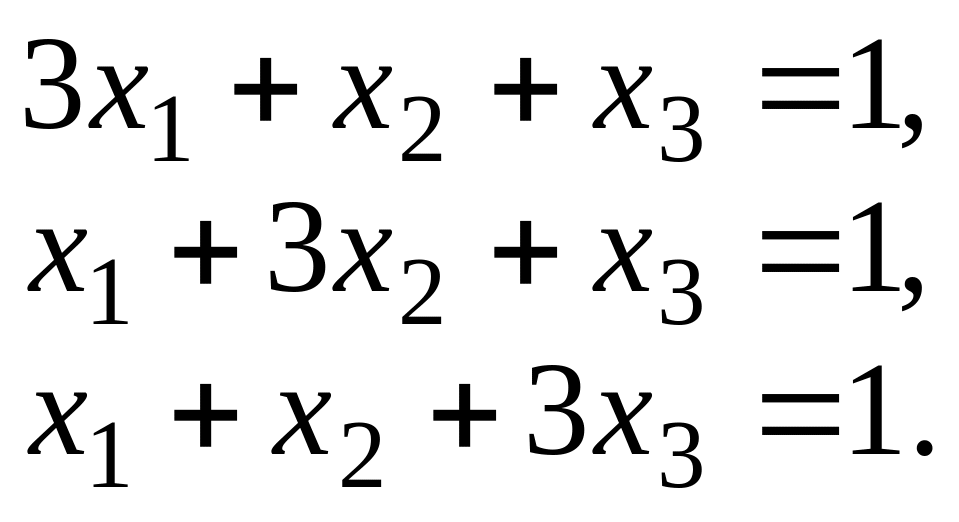 2.
2.
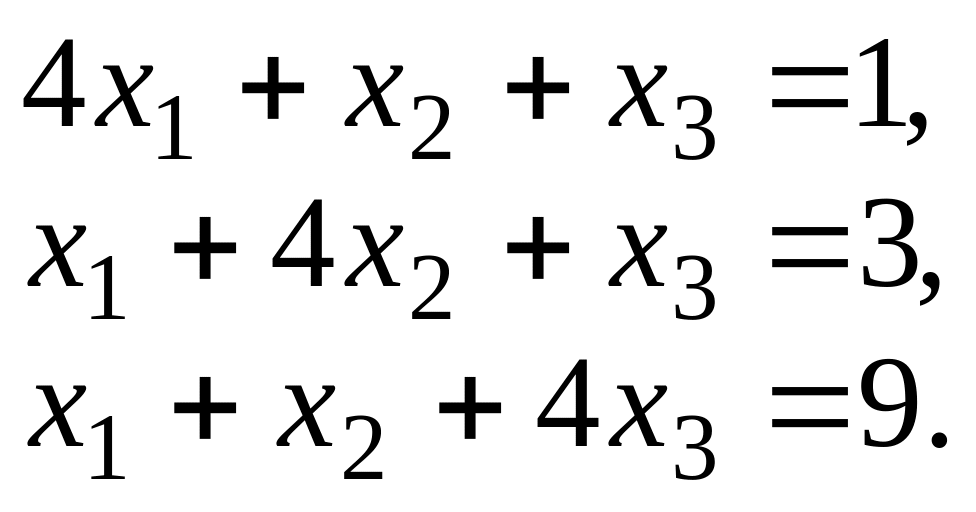
3.
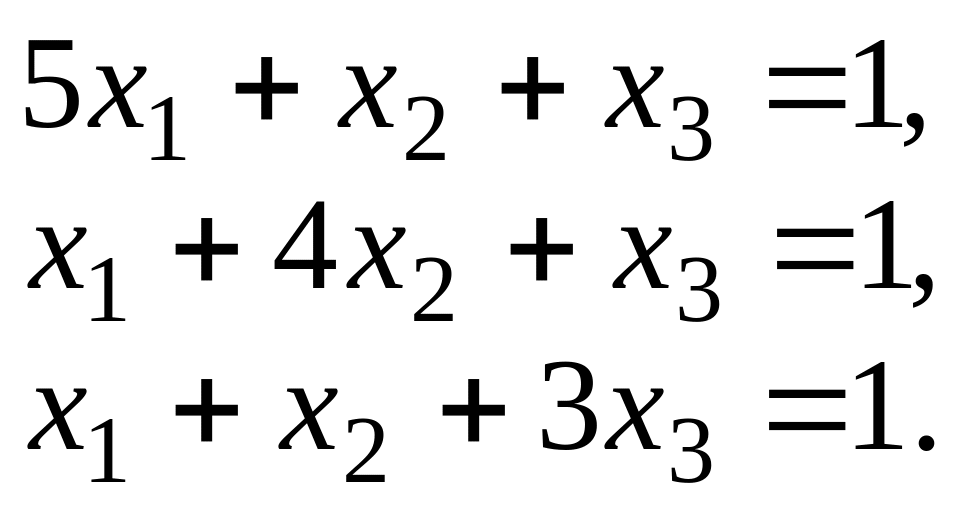 3.
3.
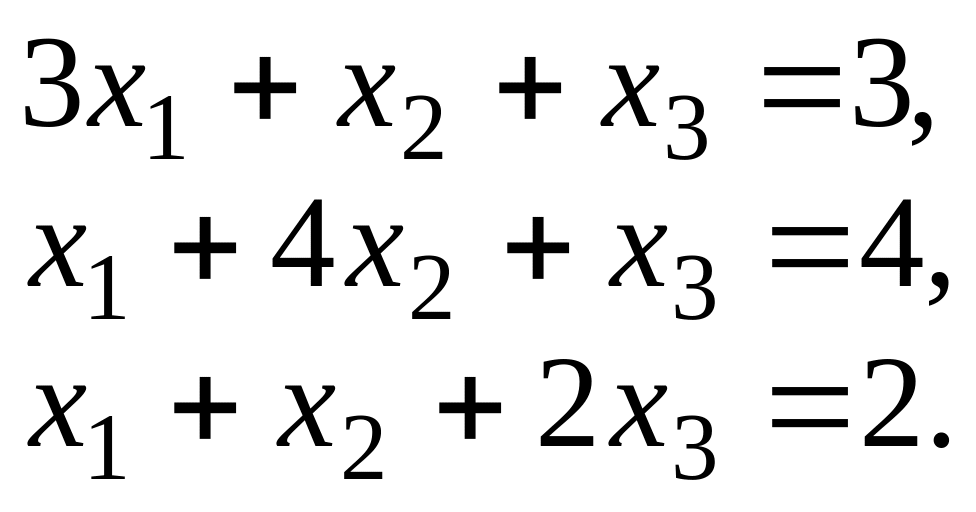
5.
 6.
6.
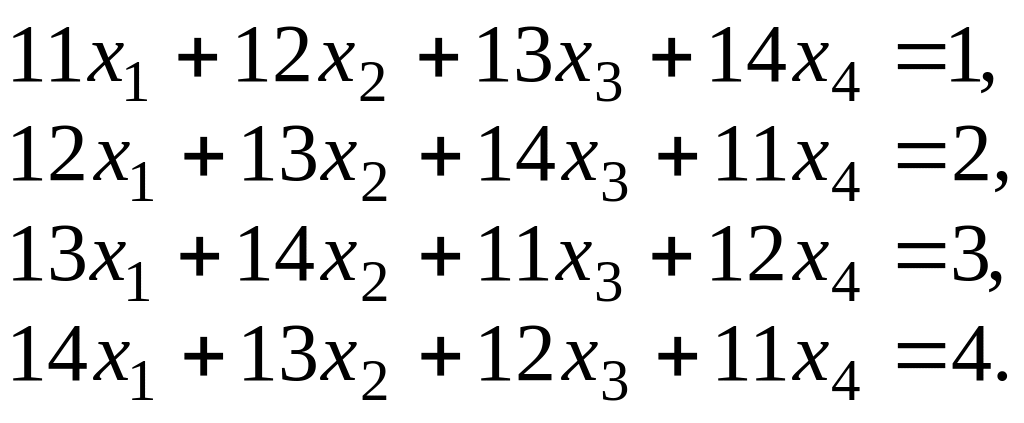
Решить системы уравнений методом Гаусса.
7.
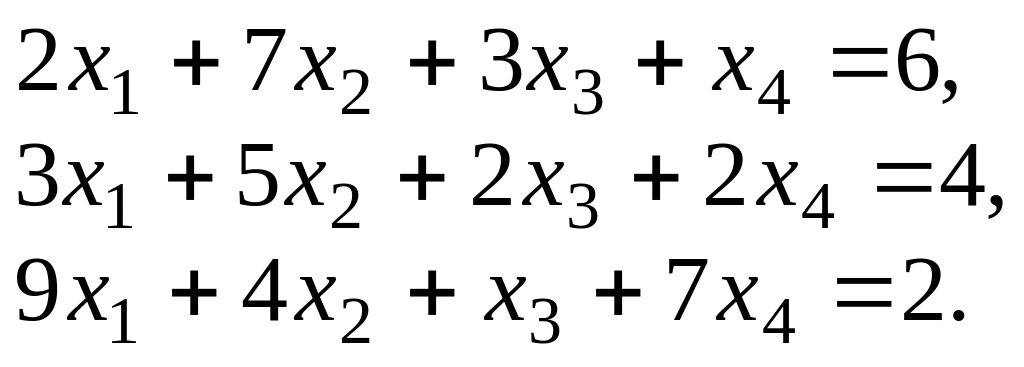 8.
8.
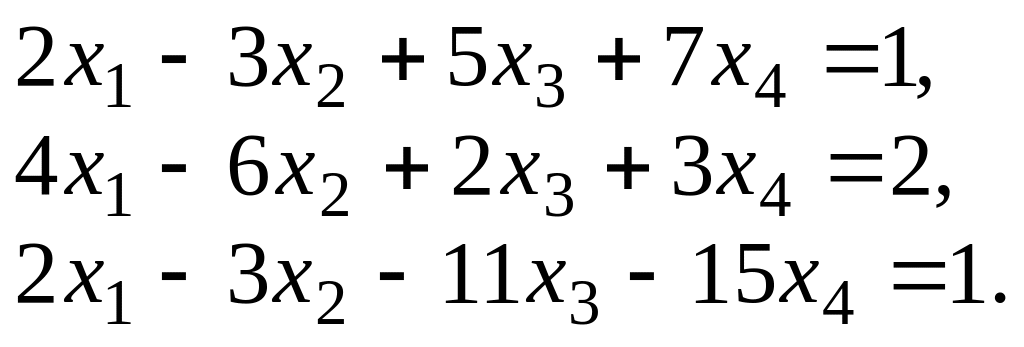
9.
 10.
10.
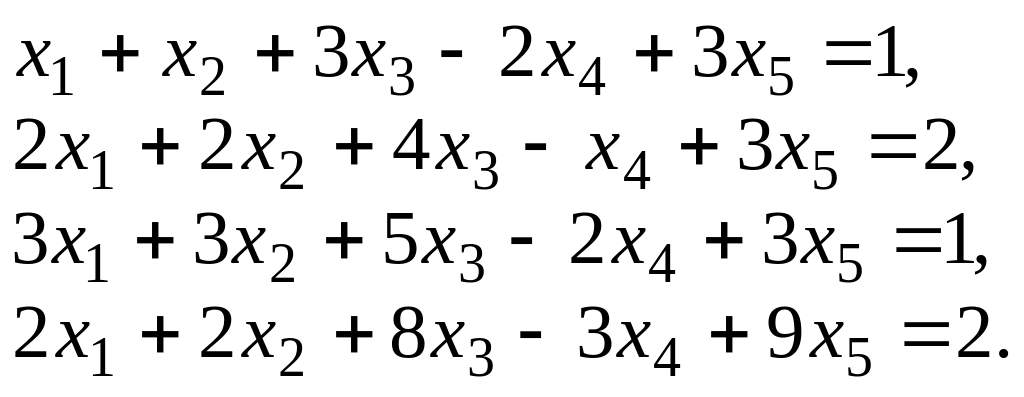
11.
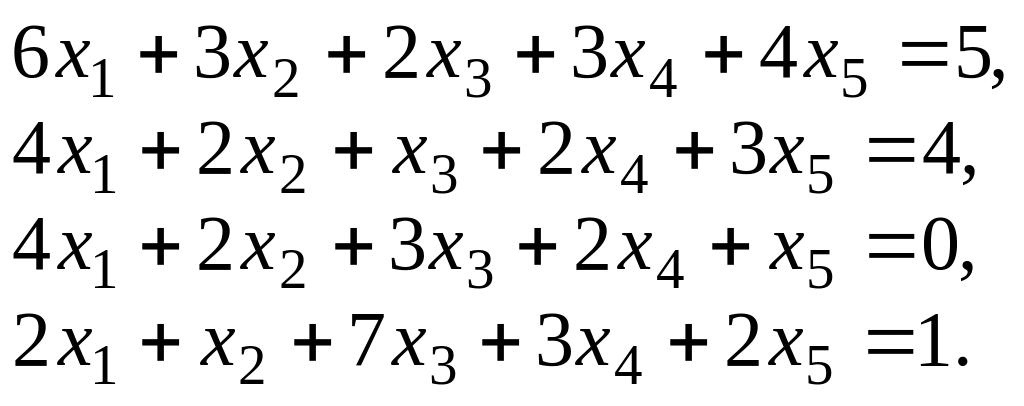
12.
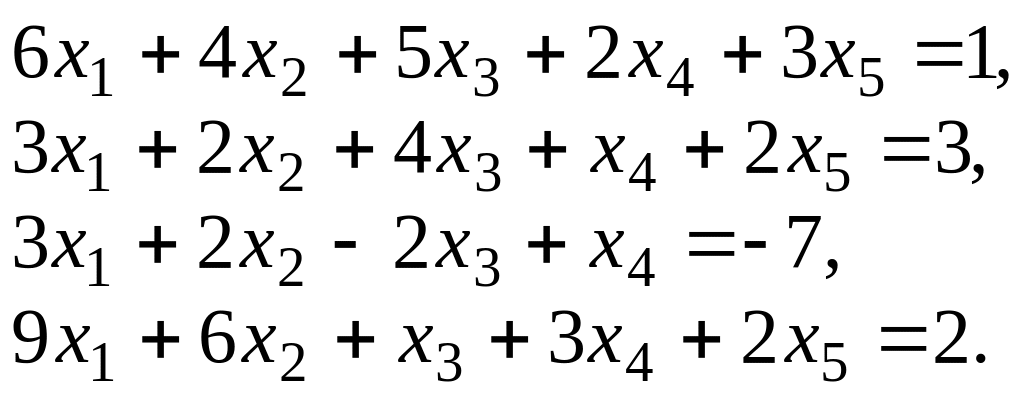
6. Однородные линейные системы
6.1. Общее решение однородной системы
Однородной линейной системой называется система уравнений вида
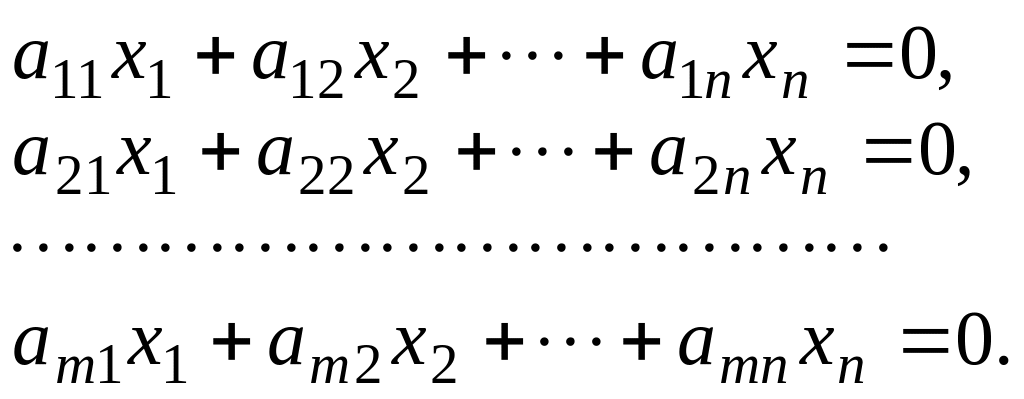
Любая однородная система совместна, так как всегда имеет нулевое (тривиальное) решение. Для существования нетривиального решения необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.
Особенностью однородной системы является то, что всякая линейная комбинация ее решений вновь является решением системы.
Определение.
Если ранг матрицы равен
,
то всякая совокупность из
![]() линейно независимых решений называется
фундаментальной
системой решений.
линейно независимых решений называется
фундаментальной
системой решений.
Для отыскания
общего решения системы достаточно найти
ее фундаментальную систему решений
![]() и составить их линейную комбинацию
и составить их линейную комбинацию
![]() .
.
Фундаментальная
система решений строится следующим
образом. Выделяем базисную систему
уравнений, главные и свободные неизвестные.
Предположим, что свободными являются
неизвестные
![]() .
Зададим определитель
порядка
.
Зададим определитель
порядка
![]() ,
отличный от нуля
,
отличный от нуля
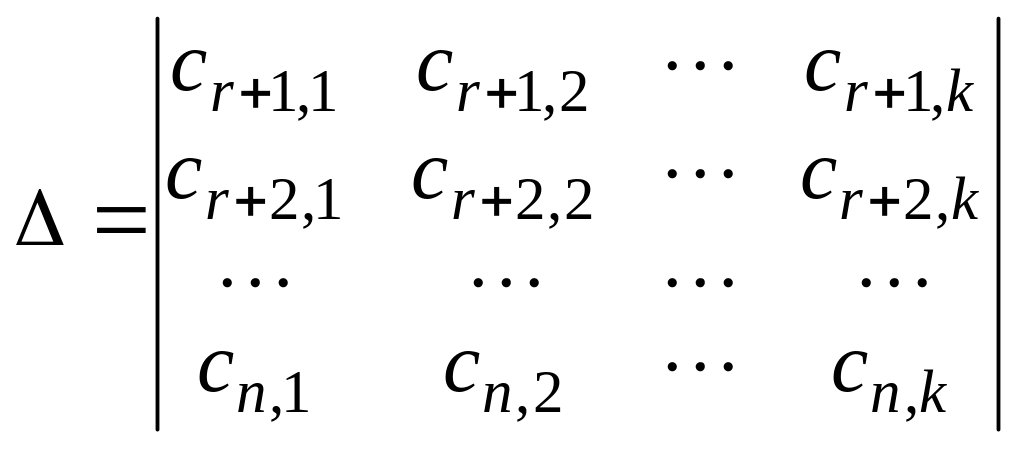 .
.
Принимая значения элементов го столбца определителя за значения свободных переменных, решаем базисную систему уравнений. Получившиеся решений образуют фундаментальную систему решений. Один из возможных вариантов выбора определителя состоит в задании его как определителя единичной матрицы
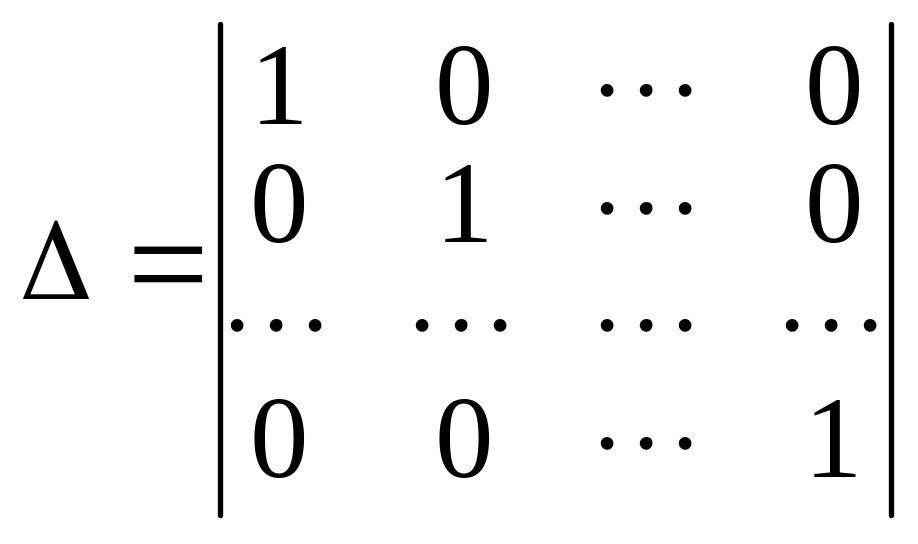 .
.
Пример. Найти фундаментальную систему решений и построить общее решение системы уравнений
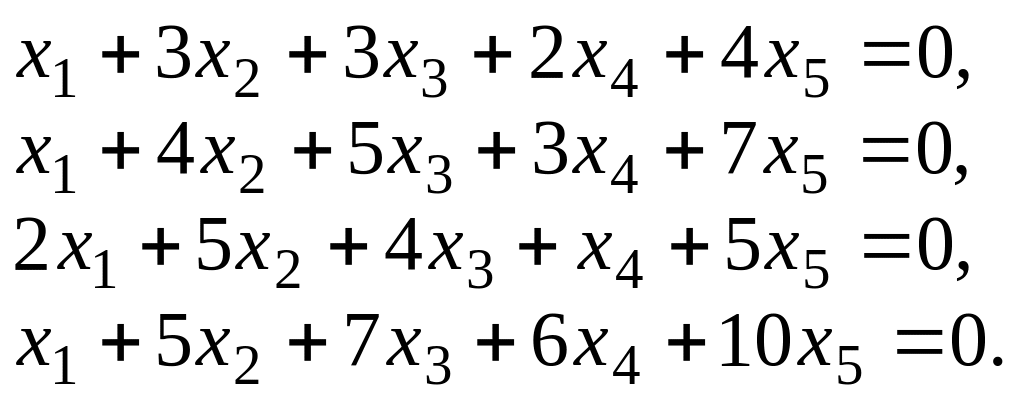
Приведем матрицу системы к ступенчатому виду
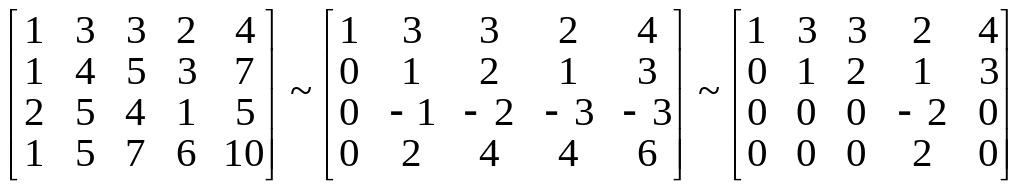 .
.
Очевидно, ранг
матрицы системы равен 3, следовательно,
фундаментальная система будет состоять
из двух решений. За главные неизвестные
можно принять
![]() ,
за свободные
,
за свободные
![]() .
Базисная система уравнений
.
Базисная система уравнений
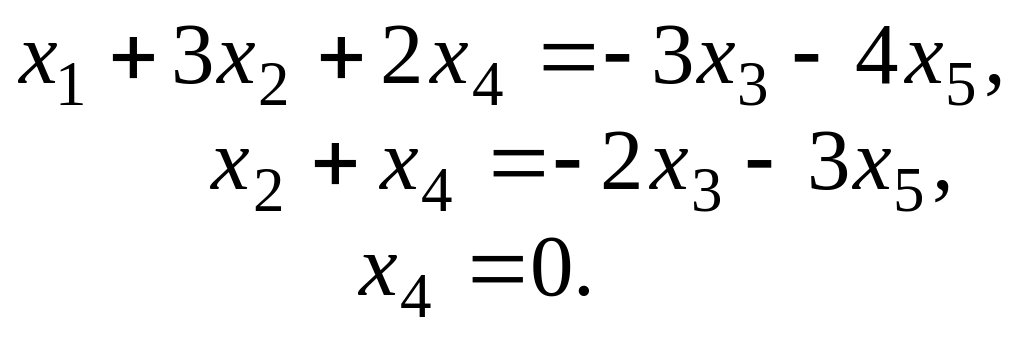
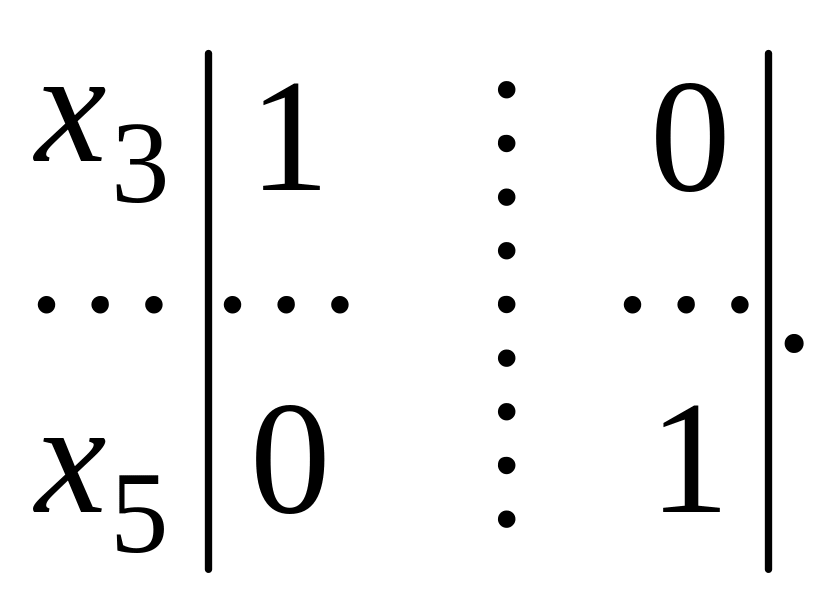
Задаем свободные
неизвестные
![]()
Решая базисную систему, получим фундаментальные решения
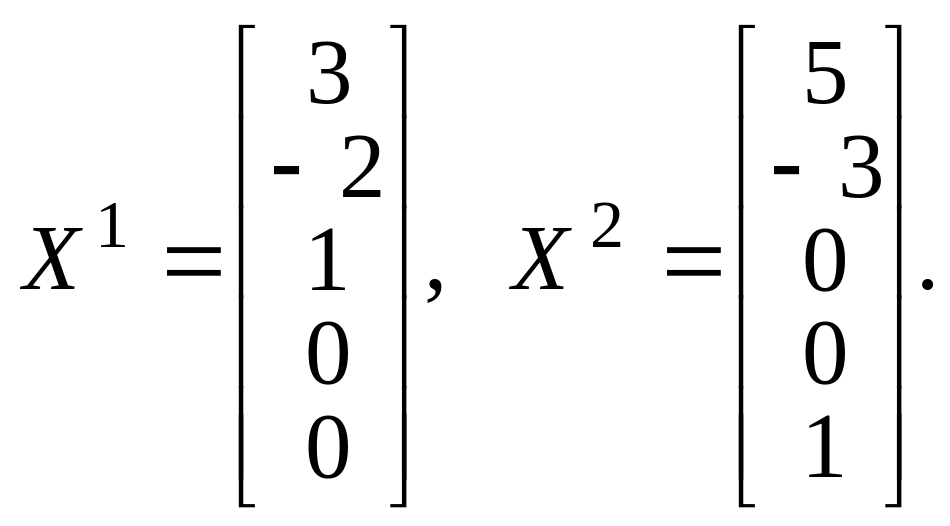
Тогда общее решение