4. Ранг матрицы

4.1. Основные понятия

Определение 1. Пусть даны вектор – столбцов порядка

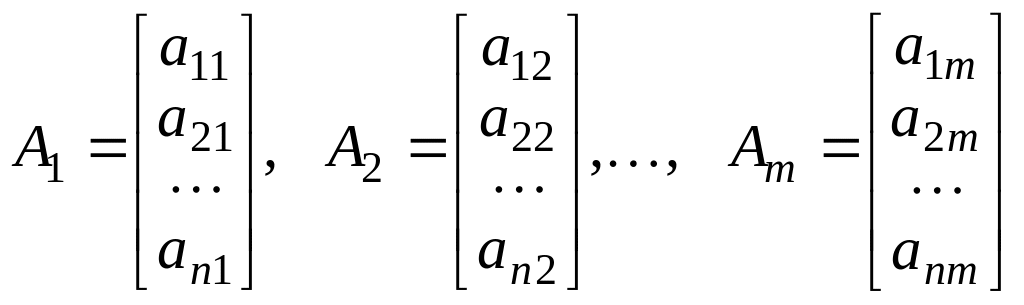
и скаляров . Умножая на и складывая, получим вектор – столбец с элементами , который называется линейной комбинацией столбцов .

Определение 2. Столбцы называются линейно зависимыми, если найдутся такие числа , не равные нулю одновременно, что линейная комбинация

,

где ноль справа это нулевой вектор – столбец.

Определение 3. Столбцы называются линейно независимыми, если равенство

возможно только при условии .

Необходимым и достаточным условием линейной зависимости вектор – столбцов является равенство одного из них линейной комбинации других.

Пример. Пусть даны вектор – столбцы

.

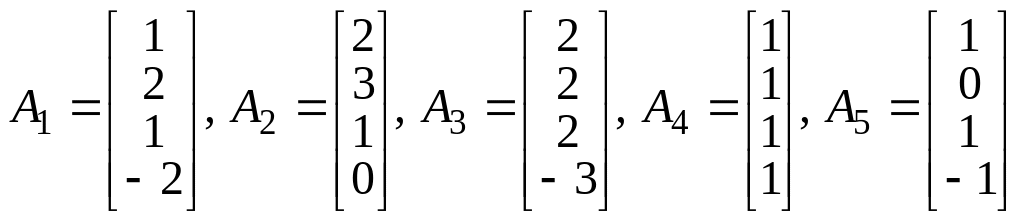Нетрудно заметить, что столбец равен сумме . Поэтому при линейная комбинация данных столбцов равна нулю и, следовательно, они линейно зависимы.

В общем случае проверка условия линейной зависимости сводится к нахождению ненулевого решения системы уравнений

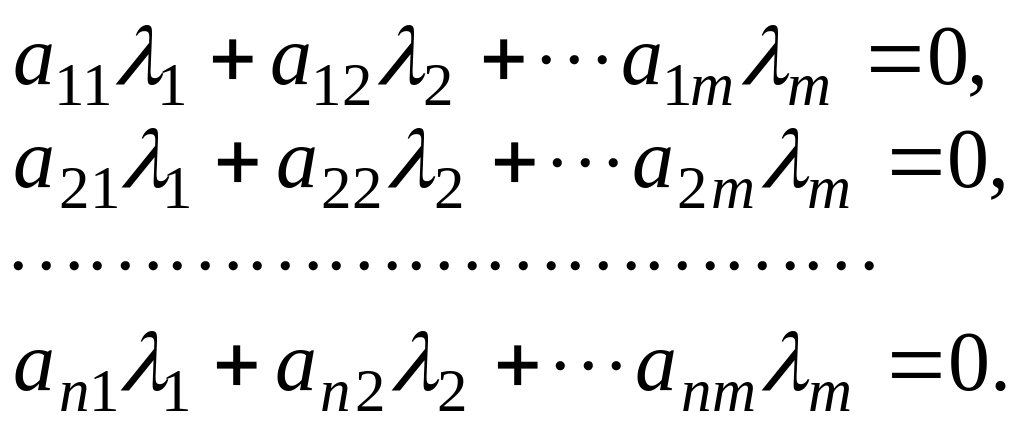
Рассмотрим теперь матрицу порядка .

Определение 4. Натуральное число называется рангом матрицы , если у нее имеется минор порядка отличный от нуля, а все миноры порядка и выше, если это возможно, равны нулю. Очевидно, что .

Определение 5. Если ранг матрицы равен , то всякий отличный от нуля минор порядка матрицы называется базисным минором. Строки и столбцы матрицы , на пересечении которых расположен базисный минор, называются базисными строками и столбцами.

Теорема (о базисном миноре). Базисные столбцы (строки) матрицы линейно независимы. Любой столбец (любая строка) матрицы является линейной комбинацией базисных столбцов (строк).

Из последних утверждений следует второе определение ранга матрицы: ранг матрицы равен максимальному числу ее линейно независимых столбцов (строк).

4.2. Вычисление ранга матрицы

Вычисление ранга матрицы можно проводить одним из следующих способов.

Первый состоит в сведении данной матрицы с помощью элементарных преобразований к канонической матрице. Каноническая матрица является блочной матрицей, у которой один из блоков представляет собой единичную матрицу, а все остальные блоки – нулевые матрицы.

Каноническую матрицу можно записать в виде

.

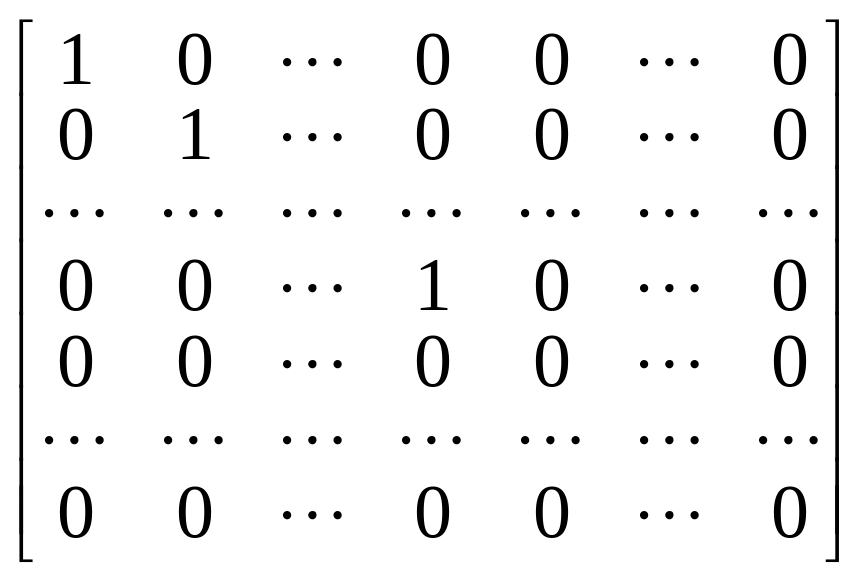Ранг канонической матрицы равен, очевидно, числу единиц, стоящих на диагонали. Преобразования, не меняющие ранга матрицы, называются элементарными. К их числу относятся:

1. Перестановка двух любых столбцов (строк) матрицы.

2. Умножение столбца (строки) на отличное от нуля число.

3. Прибавление к одному столбцу (строке) линейной комбинации других столбцов (строк).

Пример. Вычислить ранг матрицы

.

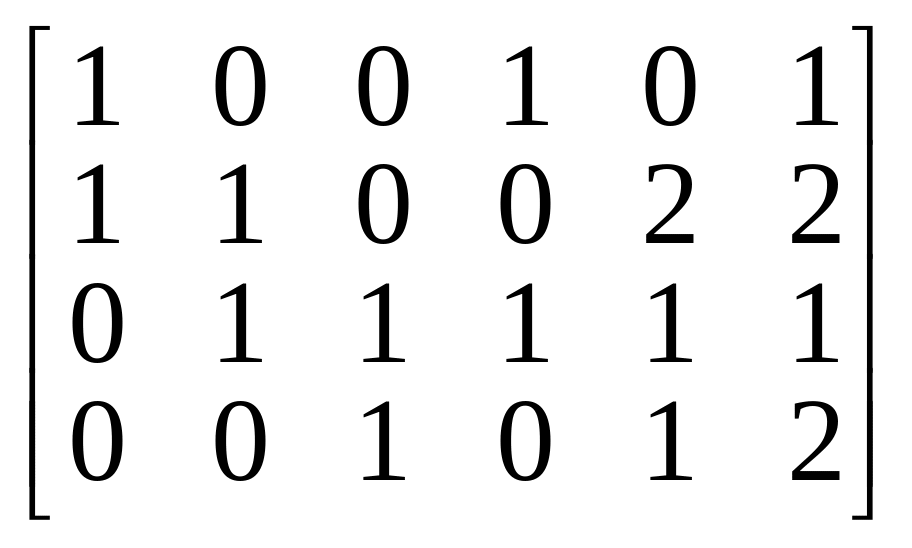Вычтем первый столбец из четвертого и шестого, а в получившейся матрице второй столбец прибавим к четвертому, вычтем его из шестого, и удвоенный второй столбец вычтем из пятого:

.

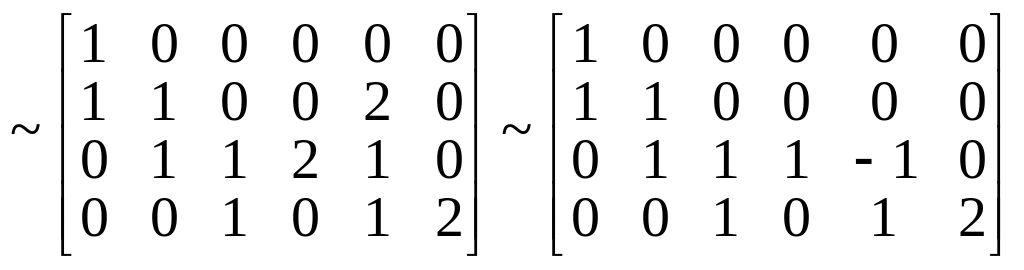В полученной матрице третий столбец прибавим к пятому и вычтем из четвертого

.

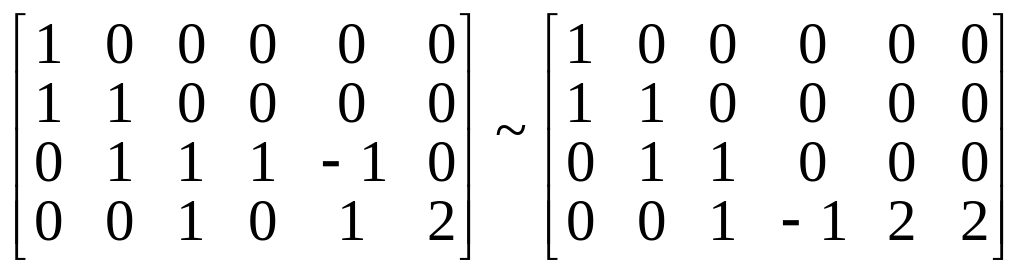Далее, четвертый столбец прибавим к третьему, удвоенный четвертый столбец прибавим к пятому и шестому. Наконец, в полученной матрице вычтем третий столбец из второго, а получившийся второй из первого

.

Ранг последней матрицы равен, очевидно, 4.

Второй способ вычисления матрицы дает метод окаймления миноров, основанный на следующей теореме:

Теорема. Пусть матрица имеет минор го порядка отличный от нуля, а все миноры го порядка, содержащие (окаймляющие) его равны нулю. Тогда ранг матрицы равен .

Пример. Вычислить ранг матрицы методом окаймления миноров

.

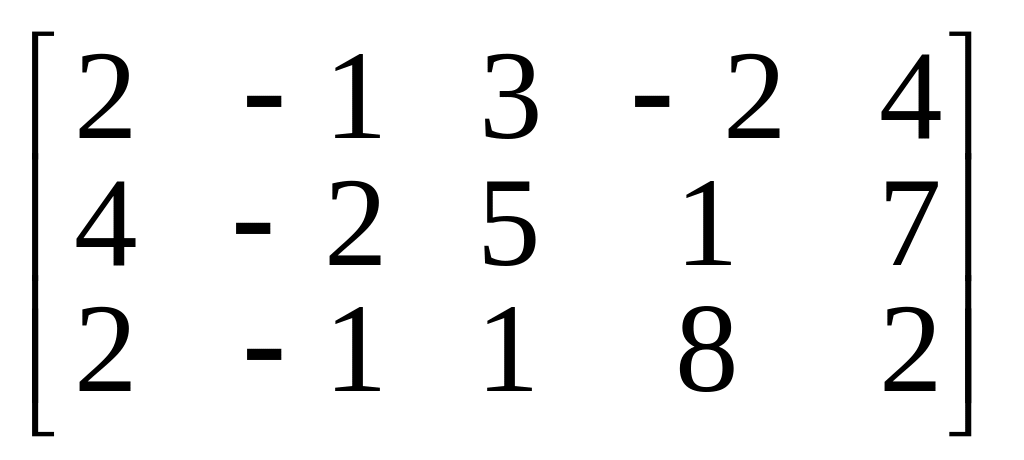У матрицы имеется минор второго порядка . Поэтому ранг данной матрицы не меньше двух. Окаймляют данный минор следующие миноры третьего порядка

.

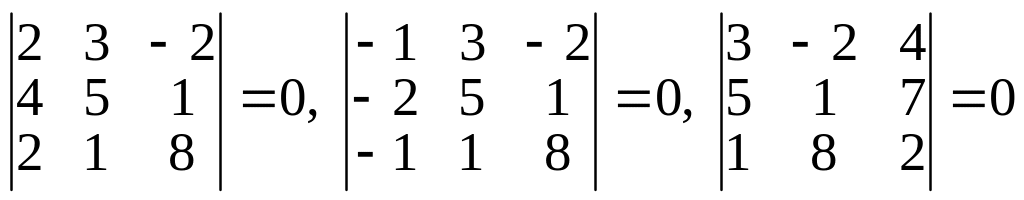Так как все они равны нулю, ранг матрицы равен двум.