Неупругое взаимодействие (соударение)

Ограничимся рассмотрением, так называемого, лобового столкновения, когда движение каждой из частиц происходит вдоль оси х (рис. 2.2).

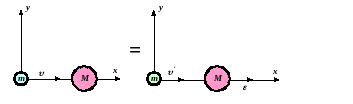Рис. 2.2. Неупругие столкновения двух частиц.

Для этого случая законы сохранения энергии и импульса запишутся в виде

, (2.11)

, (2.12) где Е_вн – изменение внутренней энергии частицы. Выражая из (2.12) V и подставляя его в (2.11), получаем для Е_вн

. (2.13)

Легко показать, что зависимость Е_вн от имеет максимум. Исследуя на максимум последнее соотношение, находим значение , при котором изменение внутренней энергии максимально

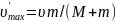. (2.14)

Подставляя (2.14) в (2.13), находим максимальное изменение внутренней энергии при неупругом взаимодействии

. (2.15)

Рассмотрим взаимодействие электрона с тяжелой частицей. Поскольку m << M, то, согласно (2.15), в случае неупругого соударения электрон может передать практически всю свою энергию. При взаимодействии частиц равных масс на изменение внутренней энергии расходуется не более половины начальной энергии частицы.

Эффективные сечения взаимодействия

Поскольку в плазме происходит большое количество различных типов взаимодействий, закономерен вопрос о важности учета того или иного процесса взаимодействия при данных условиях. Для этого следует ввести некоторый параметр, связанный с вероятностью совершения выбранного нами процесса. Таким параметром является эффективное сечение взаимодействия. Предположим (рис. 2.3), что поток частиц (например, электронов) с плотностью N (число частиц на единицу площади за 1 с) проходит вблизи частицы А (атома) и взаимодействует с ним.

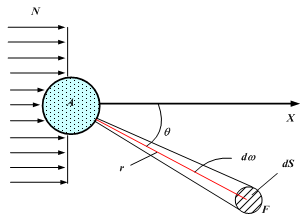
Рис.2.3. Схема, поясняющая понятие эффективное сечение взаимодействия

Под взаимодействием понимается любой возможный процесс (упругое рассеяние, рекомбинация, ионизация т.д.).

В результате этого взаимодействия частицы выбывает из потока (рассеиваются). При этом может произойти изменение внутренних состояний падающих частиц и частица А. Для простоты будем считать, что внутренне состояние изменяется только у частица А.

Рассмотрим площадку dS (рис. 2.3), расположенную на расстоянии r от частицы А. Эту площадку располагаем перпендикулярно радиус-вектору r, проведенному из центра частицы А. Угол отклонения радиус-вектора r обозначим через . Тогда телесный угол d, опирающийся на площадку dS, равен

d = dS/r² = sin dd, (2.16) где  - азимут точки F в полярной системе координат. Очевидно, что поток отклоненных частиц в единицу времени dv будет тем больше, чем больше поток падающих частиц N, чем больше телесный угол d и, кроме того, поток отклоненных частиц dv должен зависеть от некоторой вероятностной функции (, ), учитывающий как характер взаимодействия, так и направление отклонения. Таким образом, для dv можно записать

dv = Nd(, ) = N(, )sin dd. (2.17)

Так как dv имеет размерность с^-1, а N, соответственно, см^-2с^-1, то величина (, ) должна иметь размерность площади – см². Эта величина зависит от углов  и , а также от характера процесса, который в общем виде можно характеризовать как переход частицы А из состояния i в состояние j (например, i означает состояние частицы как нейтрального атома, а j – как однозарядного положительного иона, тогда переход из i в j означает ионизацию атома). Величину d_ij(, ) называют дифференциальным эффективным сечением перехода частицы А из состояния i в состояние j с отклонением падающей частицы в направлении, составляющим углы  и  по отношению к исходному. Если при взаимодействии состояние частицы А не меняется, то это означает, что взаимодействие носит упругий характер. Дифференциальное сечение для этого случая обозначается через d_ii(, ). Размерность дифференциального эффективного сечения в единицах площади позволяет определить его физический смысл следующим образом: d_ij(, ) – это часть сечения частицы А, при попадании в которое падающей частицы обязательно произойдет переход частицы А из состояния i в состояние j и падающая частица отклонится в телесный угол, определяемый направлением  и . Следует также отметить, что d_ij(, ) есть дифференциальное сечение рассеяния в единичный телесный угол.

Интегрируя d_ij(, ) по всем возможным значениям угла  от 0 до 2, получаем дифференциальное эффективное сечение частицы А при отклонении частицы в направлении 

. (2.18)

Физический смысл величины d_ij(), по аналогии с d_ij(, ), - это часть сечения частицы А, при попадании в которое падающей частицы обязательно произойдет переход частицы А из состояния i в состояние j и падающая частица отклонится в пространство между двумя конусами с углами при основании  и  +d, то есть падающая частица отклонится в телесный угол, определяемый направлением  под любым возможным значением угла .

Наконец, проинтегрировав d_ij() по всем возможным значениям угла  от 0 до 2, получим полную величину дифференциального эффективного сечения перехода

. (2.19)

Величина d_ij – это сечение частицы А, при попадании в которое падающей частицы обязательно произойдет переход частицы А из состояния i в состояние j. В большинстве случаев направление отклонения падающей частицы не очень важно, поэтому наибольшее применение имеет величина _ij . Эта величина отличается от газокинетических размеров молекулы или атома. Чаще всего она намного меньше и, кроме того, зависит от многих факторов (например, полное дифференциальное эффективное сечение ионизации атомов электронным ударом зависит от энергии электронов).

Если концентрация частиц А в рассматриваемом объеме равна n, то величина представляет собой полное сечение данного процесса. Определим физический смысл параметра Q_ij. Пусть в некотором объеме длиной l и сечением S находятся частицы A (рис. 2.4).

Рис. 2.4. Схема, поясняющая физический смысл параметра Q_ij.

Через этот объем проходят некоторые другие частицы (например, электроны), начальное количество которых N₀. Нас интересует некоторый процесс взаимодействия электронов с частицами А (например, ионизация). Зададимся вопросом: если полное дифференциальное сечение ионизации электронами частицы А есть величина _еj, то какое количество электронов пройдет данный объем, не принимая участия в ионизации?

Положим, что, претерпев ионизационное соударение, электрон выбывает из потока. Выберем в рассматриваемом объеме бесконечно тонкий участок dx, удаленный от границы этого объема на расстояние х. Этот участок настолько тонок, что частицы А не перекрывают друг друга. Пусть к этому участку доходят N_x электронов, не участвующих в ионизации. Очевидно, что для этого случая вероятность ионизации равна отношению суммарных сечений частиц А, находящихся в объеме Sdx, к его поперечному сечению S, т.е.

, (2.20)

Тогда количество электронов, участвующих в ионизации на участке dx и, соответственно, теряющихся в этой области, равно

или 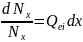. (2.21) Для определения полного количества электронов, прошедших всю область ионизации, необходимо проинтегрировать (2.21) по всей длине промежутка l

. (2.22)

На основе понятия «средняя длина свободного пробега» введем аналогичный термин «средняя длина ионизации» _ei – расстояние, которое электрон проходит между двумя ионизациями. Очевидно, что на участке dx вероятность ионизации

, (2.23)

. (2.24) Сравнивая (2.22) и (2.24), получаем

Q_ei = 1/_ei. (2.25) Таким образом, полное сечение некоторого процесса обратно пропорционально длине пробега для данного процесса и означает количество событий (ионизаций, возбуждения и т.д.), совершаемые падающей частицей на единице своего пути.

Кулоновские столкновения. Кулоновский логарифм.

Упругие взаимодействия в плазме – это, прежде всего, взаимодействия между заряженными частицами, происходящие по закону Кулона. Поэтому их называют кулоновскими взаимодействиями. Эти взаимодействия играют важную роль в плазменных процессах. Кроме них, в низкотемпературной слабоионизованной плазме следует учитывать упругие рассеяния заряженных частиц на нейтральных атомах и молекулах, так же как и столкновения нейтральных частиц между собой.

Рассмотрим более подробно кулоновские взаимодействия. Начнем изучение кулоновских столкновений с рассмотрения следующей задачи: пусть на кулоновский центр заряда q₂e налетает поток частиц j с зарядом q₁e (рис. 2.5). Вычислим силу, действующую на рассеивающий центр.

Рис. 2.5. Траектория заряда q₁e, рассеивающегося на неподвижном кулоновском центре q₂e

Пусть  обозначает прицельное расстояние налетающей частицы. Через колечко площадью 2d в единицу времени пролетает 2dj частиц. Каждая частица отклоняется на угол , зависящий от прицельного расстояния , и передает рассеивающему центру продольный импульс

p_|| = m(1 - cos).

Искомая сила F будет направлена вдоль скорости налетающего потока частиц и равна импульсу, передаваемому рассеивающему центру в единицу времени,

, (2.26) где

. (2.27)

Параметр _тр называется транспортным сечением и имеет смысл площади поперечного сечения, которое имеет рассеивающий центр, если бы он полностью поглощал импульс падающих на него частиц.

Для того чтобы вычислить интеграл (2.27), необходимо знать зависимость  от . Эта зависимость легко находится в приближении далеких пролетов, т.е. когда прицельное расстояние настолько велико, что угол  можно считать малым,  << 1. В таком приближении можно также считать, что частица движется по прямой с постоянной скоростью , и найти изменение ее поперечного импульса, проинтегрировав перпендикулярную к траектории составляющую кулоновской силы по времени:

.

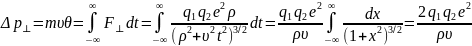Отсюда находим

. (2.28) Точная формула Резерфорда, дающая зависимость  от  при любых , ненамного сложнее (2.28):

. (2.29) Возвращаясь к интегралу (2.27), отметим, что основной вклад в него будут вносить большие расстояния, где как раз и справедливо приближение далеких пролетов. Пользуясь разложением

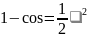
И формулой (2.29), из (2.28) находим

. (2.30) Как видно, данный интеграл логарифмически расходится на нижнем и верхнем пределах. Расходимость при малых  связана с тем, что здесь нарушается использованное нами приближение далеких пролетов. Этой расходимости не возникло, если бы мы пользовались точным выражением (2.29). Исправить положение можно, заменив нижний предел интегрирования в (2.30) на минимальное расстояние _min, при котором еще можно пользоваться нашим приближением. Поскольку интеграл (2.30) зависит от нижнего предела только логарифмически, то точное значение _min не очень существенно. В качестве _min можно выбрать то прицельное расстояние, при котором происходит рассеяние на угол порядка /2:

. (2.31) Расходимость при больших значениях  носит более глубокую причину. Она связана с тем обстоятельством, что кулоновский потенциал слишком медленно убывает с расстоянием. Однако, как мы уже знаем, на самом деле в плазме потенциал заряда экранируется, так что на расстояниях, больших чем дебаевский радиус r_D, поле спадает экспоненциально. Учет этого обстоятельства приводит к тому, что прицельные расстояния, большие r_D, фактически не вносят вклад в (2.30), и поэтому в качестве верхнего предела _max в интеграле можно взять величину r_D:

. (2.32) Точное значение отношения _max./_min не очень существенно, поскольку оно входит под знаком логарифма (по этой причине мы не учитывали также, что на самом деле поле заряда в плазме является не кулоновским, а «экранированным кулоновским»; учет этого обстоятельства дал бы множитель порядка единицы под знаком логарифма).

Величину

(2.33) называют кулоновским логарифмом. Важно отметить, что под знаком логарифма в (2.33) стоит большое число. Действительно, положим для оценки ² = 3T/m, q₁ = q₂ = 1, тогда

.

Для плазмы с Т = 100 эВ, n =10¹⁴ см^-3 находим

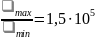,  = 14,3.

Обычно в качестве  берут число 10 – 15. Итак, для величины _тр мы получаем выражение

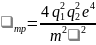. (2.34) Это сечение падает обратно пропорционально квадрату энергии налетающих частиц E = m²/2. Принимая q₁ =q₂ = 1 и  = 15, получим практическую формулу

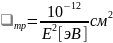. (2.35)