Лекція 11

Нормальні форми матриці Нормальна форма Жордана

Як відомо, до діагонального вигляду зводиться матриця не кожного лінійного перетворення. Тому виникає питання про інший канонічний вигляд, до якого можна звести матрицю довільного лінійного перетворення. В алгебраїчно замкненому полі, в тому числі і комплексному просторі, канонічним виглядом довільної матриці є так звана жорданова нормальна форма матриці. Розглянемо її.

Жордановою кліткою називається квадратна матриця вигляду

,

в якій на головній діагоналі знаходиться одне і те ж число , над головною діагоналлю – всюди число , а всі решта елементи – нулі.

Наприклад: , , – жорданові клітки 1, 2 і 3 порядків.

Легко видно, що характеристичний многочлен | - | перетворення , матрицею якого є жорданова клітка порядку , дорівнює . Він має єдине власне значення кратності , тому всі його власні вектори колінеарні (“спів- напрямлені” з e₁), тобто не утворюють лінійно незалежної системи. Це означає, що матриця перетворення при ні в якому базисі не зводиться до діагональ-ного вигляду (не існує власного базису).

Жордановою матрицею називається матриця вигляду

,

де – жорданові клітки деяких (не обов’язково різних) порядків, всі інші клітки заповнені нулями. Числа є власними значеннями перетворення з матрицею .

Діагональні матриці є частинним випадком жорданових матриць (у них жорданові клітки мають порядок 1).

Квадратні матриці порядку , елементами яких є многочлени довільних степенів від однієї невідомої з коефіцієнтами із поля Р, називаються многочленними матрицями або -матрицями.

-матриці А( )та В( ) називаються еквівалентними, якщо від матриці А( ) до матриці В( ) можна перейти шляхом скінченої кількості елементарних перетворень.

Канонічною -матрицею називається -матриця, яка володіє властивостями:

1) ця матриця є діагональною, тобто має вигляд ;

2) всякий многочлен е_і(λ) націло ділиться на многочлен е_і-1(λ);

3) кожний многочлен е_і(λ)є зведеним.

Теорема 1. Будь-яка -матриця з допомогою елементарних перетворень зводиться до канонічного вигляду, причому однозначно.

Доведення.

Нехай задана довільна -матриця А( ) порядку . Зафіксуємо деяке число k і відшукаємо всі мінори k-го порядку матриці А( ). Отримаємо скінченну систему многочленів від . НСД цієї системи многочленів (у зведеному вигляді) позначимо через d_к( ). Таким способом отримаємо однозначно визначену множину многочленів

d₁( ), d₂( ), , d_n( ) (1).

Якщо матриця А( ) має ранг r, то d_r+1( ) = = d_n( )= 0.

d_к( ) не змінюється при виконанні в матриці А( ) елементарних перетворень.

Отже, всім -матрицям , еквівалентним матриці А( ) , відповідає один і той же набір многочленів (1), тому для знаходження цих многочленів скористаємось канонічною (найпростішою) матрицею. Ясно, що мінор k-го порядку, який знаходиться в лівому верхньому куті матриці, дорівнює добутку е₁(λ) е₂(λ) ···е_к(λ) (2).

Якщо, далі, ми беремо в канонічній матриці мінор k-го порядку, який знаходиться в рядках з номерами i₁, i₂,...i_k (де i₁‹ i₂‹…‹ i_k) і в стовпчиках з тими ж номерами, то цей мінор дорівнює добутку , який ділиться на (2), оскільки із із і т. д.

Нарешті, якщо в канонічній матриці взято мінор k-го порядку, в якому номери рядків і стовпчиків не співпадають, то цей мінор містить нульовий рядок і тому дорівнює нулю. У підсумку випливає, що добуток (2) і буде НСД всіх мінорів k-го порядку канонічної матриці, а, значить, і вихідної матриці А( ).

d_k(λ) = е₁(λ) е₂(λ) ···е_к(λ), k=1,2, n. (3).

Ясно, що d_k-1(λ) = е₁(λ) е₂(λ) ···е_к-1(λ).

Із єдиності набору многочленів (1) випливає однозначність визначення многочленів е_k(λ).

Нехай ранг матриці А( ) дорівнює r. Тоді d_r(λ)≠0, але d_r+1( )= 0, звідки

е_r+1 (λ)= 0. (із 3). Звідси, якщо r ‹ n, то е_r+1 (λ)= е_n (λ) = 0, З другого боку, якщо k ≤ r, то (4).

Ми отримали спосіб безпосереднього знаходження многочленів е_k(λ), які називаються інваріантними множниками матриці А( ). ▲

Мінімальним многочленом матриці називається зведений незвідний многочлен, для якого ця матриця є коренем.

Знайдемо канонічний вигляд для характеристичної матриці довільної жорданової матриці порядку . Спочатку зробимо це для характеристичної матриці однієї жорданової клітки порядку .

Нехай є НСД мінорів порядку i матриці I зведеними многочленами від λ. Зокрема, .

Обчислюючи визначник цієї матриці і пам’ятаючи, що старший коефіцієнт многочлена має бути рівним , одержуємо, що . З другого боку, серед мінорів -го порядку матриці є мінор, рівний , а саме той, що отримується після закреслення першого стовпця і останнього рядка цієї матриці. Тому . Звідси випливає, що канонічним виглядом для клітки є така -матриця -го порядку:

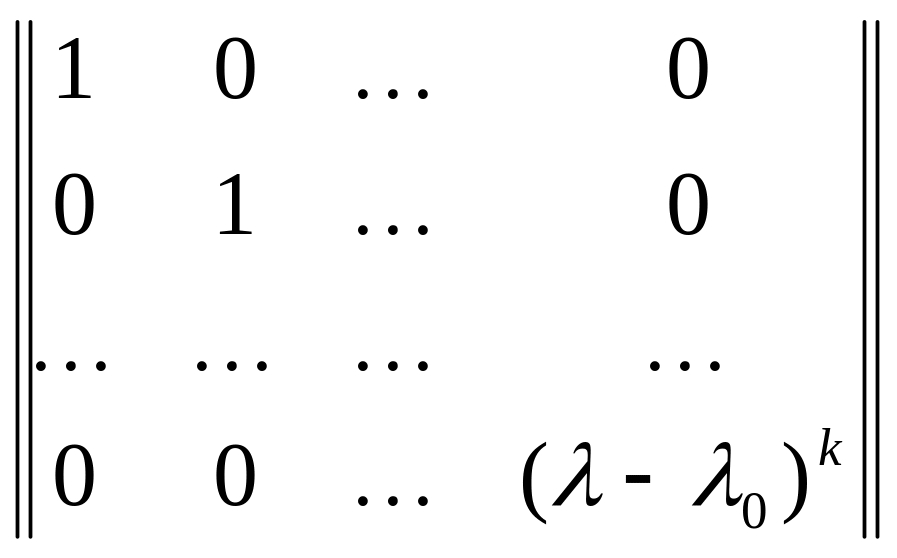. (5)

Теорема 2. Якщо многочлени із кільця – попарно взаємно прості, то має місце така еквівалентність:

~ .