Результат работы алгоритма:
A =
-0.6800 -0.1800 0.0200 0.2100
0.1600 -0.8800 -0.1400 0.2700
0.3700 0.2700 -1.0200 -0.2400
0.1200 0.2100 -0.1800 -0.7500
B =
-1.8300
0.6500
-2.2300
1.1300
L =
1.0000 0 0 0
-0.2353 1.0000 0 0
-0.5441 -0.1865 1.0000 0
-0.1765 -0.1932 0.1959 1.0000
U =
-0.6800 -0.1800 0.0200 0.2100
0 -0.9224 -0.1353 0.3194
0 0 -1.0344 -0.0662
0 0 0 -0.6383
X =
2.4731
-1.5106
3.2266
-2.3083
3. Метод вращений решения.
Целью прямого хода преобразований метода вращений заключается в приведение системы к треугольному виду последовательным обнулением поддиагональных элементов сначала первого столбца, затем второго и т.д.
В результате (n-1) этапов прямого хода исходная система будет приведена к треугольному виду
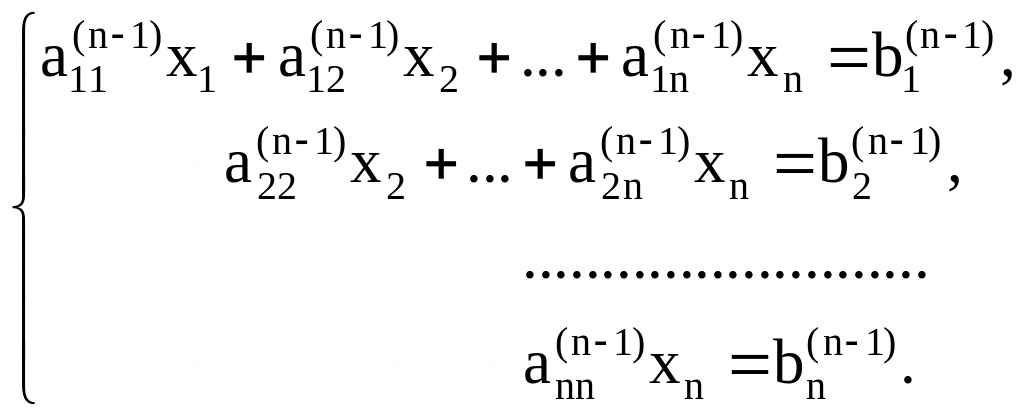
Нахождение
отсюда неизвестных
не отличается от обратного хода метода
Гаусса.
Практическая часть (листинг программы MatLab)
function Rotation
A=[-0.68 -0.18 0.02 0.21 -1.83;
0.16 -0.88 -0.14 0.27 0.65;
0.37 0.27 -1.02 -0.24 -2.23;
0.12 0.21 -0.18 -0.75 1.13];
X=zeros(4,1);
iter=0;
C1=A(1,1)/sqrt((A(1,1))^2+(A(2,1))^2);
S1=A(2,1)/sqrt((A(1,1))^2+(A(2,1))^2);
T=A;
for j=1:5
iter=iter+1;
A(1,j)=C1* T (1,j)+S1* T (2,j);
A(2,j)=-S1* T (1,j)+C1* T (2,j);
end
C2=A(1,1)/sqrt((A(1,1))^2+(A(3,1))^2);
S2=A(3,1)/sqrt((A(1,1))^2+(A(3,1))^2);
T=A;
for j=1:5
iter=iter+1;
A(1,j)=C2* T (1,j)+S2* T (3,j);
A(3,j)=-S2* T (1,j)+C2* T (3,j);
end
C3=A(1,1)/sqrt((A(1,1))^2+(A(4,1))^2);
S3=A(4,1)/sqrt((A(1,1))^2+(A(4,1))^2);
T=A;
for j=1:5
iter=iter+1;
A(1,j)=C3* T (1,j)+S3* T (4,j);
A(4,j)=-S3* T (1,j)+C3* T (4,j);
end
C4=A(2,2)/sqrt((A(2,2))^2+(A(3,2))^2);
S4=A(3,2)/sqrt((A(2,2))^2+(A(3,2))^2);
T=A;
for j=2:5
iter=iter+1;
A(2,j)=C4* T (2,j)+S4* T (3,j);
A(3,j)=-S4* T (2,j)+C4* T (3,j);
end
C5=A(2,2)/sqrt((A(2,2))^2+(A(4,2))^2);
S5=A(4,2)/sqrt((A(2,2))^2+(A(4,2))^2);
T=A;
for j=2:5
iter=iter+1;
A(2,j)=C5* T (2,j)+S5* T (4,j);
A(4,j)=-S5* T (2,j)+C5* T (4,j);
end
C6=A(3,3)/sqrt((A(3,3))^2+(A(4,3))^2);
S6=A(4,3)/sqrt((A(3,3))^2+(A(4,3))^2);
T=A;
for j=3:5
iter=iter+1;
A(3,j)=C6* T (3,j)+S6* T (4,j);
A(4,j)=-S6* T (3,j)+C6* T (4,j);
end
X(4)=A(4,5)/A(4,4);
X(3)=(A(3,5)-A(3,4)*X(4))/A(3,3);
X(2)=(A(2,5)-A(2,4)*X(4)-A(2,3)*X(3))/A(2,2);
X(1)=(A(1,5)-A(1,4)*X(4)-A(1,3)*X(3)-A(1,2)*X(2))/A(1,1);
X
Результат работы алгоритма:
>> Rot
A =
0.7996 0.1334 -0.5440 -0.3482 0.8241
-0.0000 0.9518 -0.1271 -0.4741 -0.7537
0 -0.0000 0.8835 0.1092 2.5988
0.0000 -0.0000 0 0.6158 -1.4214
X =
2.4731
-1.5106
3.2266
-2.3083
4. Метод простых итераций.
Дана система стандартного вида:
Ax=b, (1)
где
-
-матрица
,
-
n-мерные
векторы-столбцы, тем или иным способом
может быть преобразована к эквивалентной
ей системе вида:
(2),
где x – тот же вектор неизвестных,
B и c – некоторые новые матрица и вектор соответственно.
Систему
(2) - как задача о неподвижной точке
линейного отображения B
в пространство
и по аналогии со скалярным случаем
определить последовательность приближений
к неподвижной точке
рекуррентным равенством
(3).
Итерационный процесс (3), начинающийся
с некоторого вектора
- методом простых итераций (МПИ).
Лемма 1: условие, что все собственные числа матрицы B по модулю меньше 1, является необходимым и достаточным для того, чтобы:
1.
при
2.
матрица
имела обратную и
.
Лемма
2: если
,
то матрица
имеет обратную матрицу
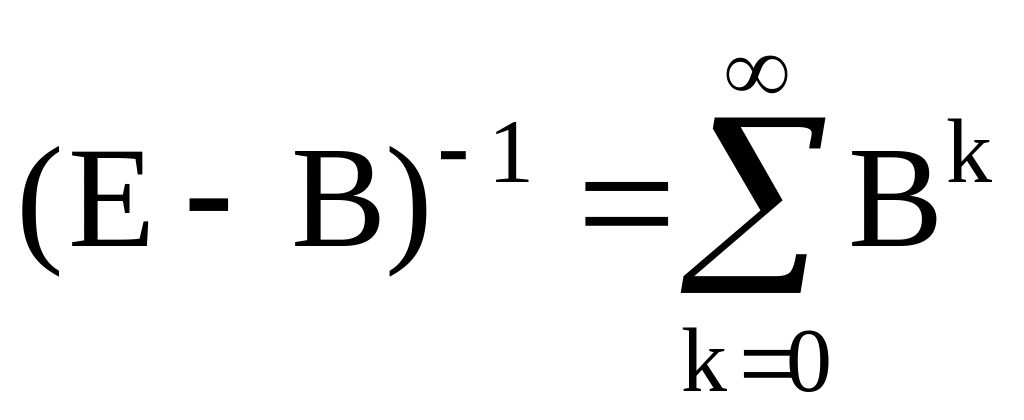и при этом справедливо неравенство
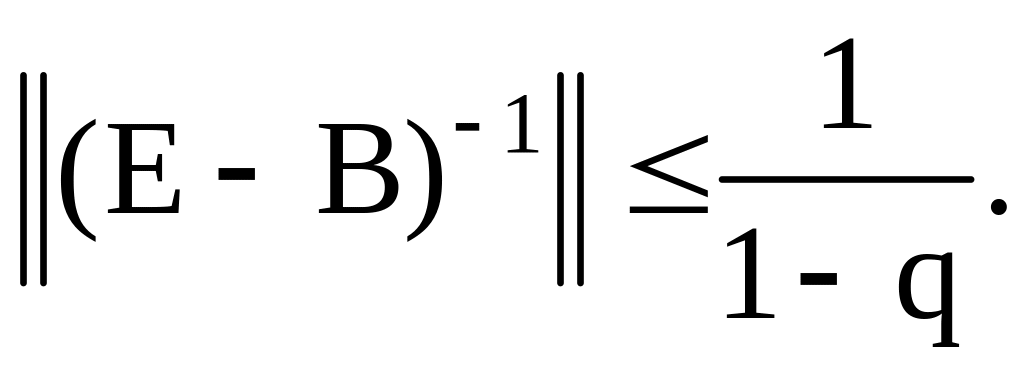
Теорема
1: необходимым
и достаточным условием сходимости
метода простых итераций (3) при любом
начальном векторе
к решению
системы (2) является требование, чтобы
все собственные числа матрицы B
были по модулю меньше 1.
Теорема
2: пусть
Тогда при любом начальном векторе
МПИ (3) сходится к единственному решению
задачи (2) и при всех
справедливы оценки погрешности:
1.
апостериорная:
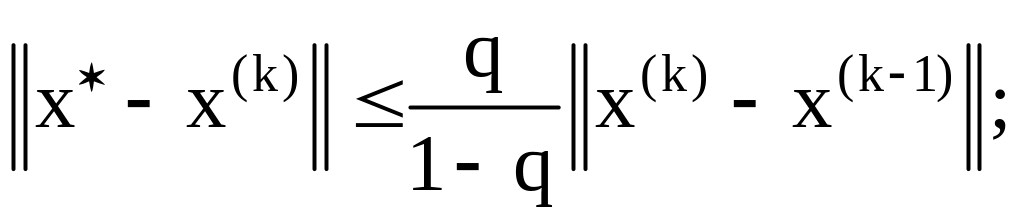
2.
априорная:
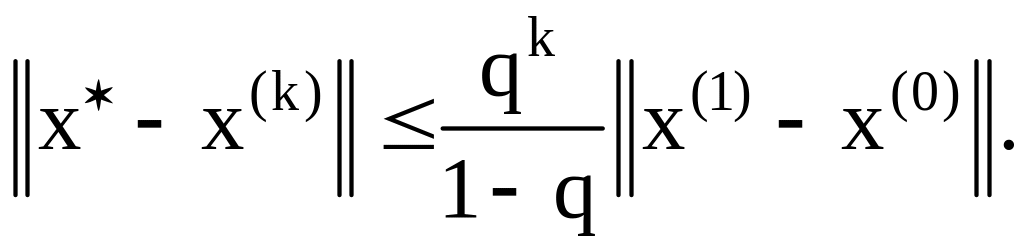
Критерий
сходимости МПИ: Для
того, чтобы МПИ был сходящимся при любом
начальном приближении необходимо и
достаточно, чтобы все собственные числа
матрицы
были по модулю меньше 1.
Условие
останова
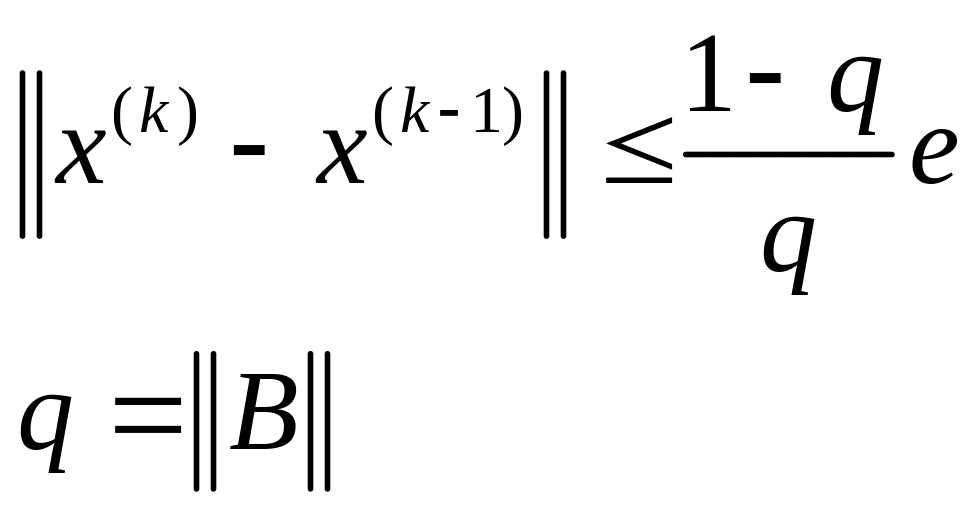
Практическая часть (листинг программы MatLab)
function mpi_slau
b=[-1.83; 0.65; -2.23; 1.13];
A=[-0.68 -0.18 0.02 0.21;
0.16 -0.88 -0.14 0.27;
0.37 0.27 -1.02 -0.24;
0.12 0.21 -0.18 -0.75 ];
condA=cond(A);
condA
e=[1 1 1 1];
E=diag(e);
B=A+E;
c=b;
q=norm(B,1);
q
X=[0;0;0;0];
X_k1=[0;0;0;0];
X_k=[0;0;0;0];
X_k=B*X_k+c;
n=max(abs(X_k-X_k1));
i=1;
while n > (((1-q)/q)*eps)
X_k1=X_k;
X_k=B*X_k+c;
n=max(abs(X_k-X_k1));
i=i+1;
end
X=X_k
disp('итераций'), i