
- •Зав. Кафедрой________________а.А.Трещев
- •Зав. Кафедрой________________а.А.Трещев
- •1. Первичная статистическая обработка эксперимента Задание на практическое занятие
- •Порядок выполнения
- •Содержание отчета
- •Контрольные вопросы
- •Вступление в теорию планирования эксперимента
- •Объект исследования
- •Факторное пространство
- •Проведение эксперимента
- •Пример выполнения
- •2. Интервальные оценки числовых характеристик
- •Пример 2.1 (Matlab)
- •Пример 4.4 (Maple)
- •Задание
- •Контрольные вопросы
- •3. Критерии согласия
- •Пример 3.1 (Matlab)
- •Пример 3.2 (Maple)
- •Задание
- •Контрольные вопросы
- •4. Метод наименьших квадратов
- •Пример 4.1 (Maple)
- •Пример 4.2 (Matlab)
- •Задание
- •Контрольные вопросы
- •5. Обработка результатов эксперимента Задание на практическое занятие
- •Порядок выполнения
- •Проверить однородность дисперсии по критерию Кохрена
- •Содержание отчета
- •Контрольные вопросы
- •Теоретические сведения Нахождение построчной дисперсии
- •Проверка однородности по критерию Кохрэна
- •Проверка нуль - гипотезы по критерию Стьюдента
- •Проверка адекватности по критерию Фишера
- •Пример выполнения
- •Библиографический список рекомендуемой литературы
Контрольные вопросы
Что называется доверительным интервалом и доверительной вероятностью?
Дайте общую схему построения доверительного интервала.
Как изменяется доверительный интервал с увеличением надежности? С увеличением объема выборки?
Как изменяется доверительный интервал в зависимости от того, известны ли другие параметры точно или нет?
3. Критерии согласия
Допустим,
что построенную по выборке статистическую
функцию распределения
![]() мы сгладили с помощью некоторой
гипотетической функции распределения
мы сгладили с помощью некоторой
гипотетической функции распределения
![]() .
Возникает вопрос: а верна ли гипотеза
о том, что функция распределения именно
,
а не какая-либо
другая?
Точнее, не противоречит ли гипотеза о
законе распределения
результатам эксперимента?
Чтобы
ответить на этот вопрос, пользуются
критериями согласия.
.
Возникает вопрос: а верна ли гипотеза
о том, что функция распределения именно
,
а не какая-либо
другая?
Точнее, не противоречит ли гипотеза о
законе распределения
результатам эксперимента?
Чтобы
ответить на этот вопрос, пользуются
критериями согласия.
Под
критерием согласия понимают некоторую
величину
![]() ,
которая отражает количественную меру
расхождения гипотетического
и эмпирического
распределений. Эту величину можно
выбрать многими способами, в соответствии
с которыми получаются и различные
критерии проверки интересующей нас
гипотезы. Например, можно положить
,
которая отражает количественную меру
расхождения гипотетического
и эмпирического
распределений. Эту величину можно
выбрать многими способами, в соответствии
с которыми получаются и различные
критерии проверки интересующей нас
гипотезы. Например, можно положить
![]()
или
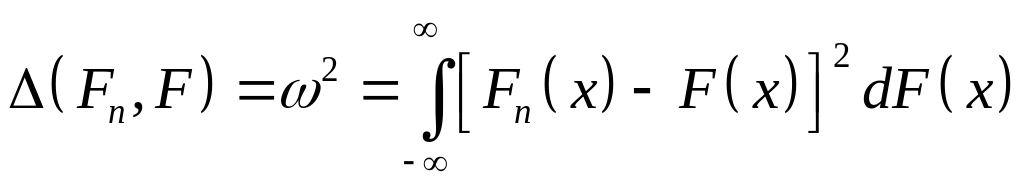
В первом случае получаем критерий Колмогорова, во втором – критерий Мизеса.
Схема
применения критерия согласия следующая.
Возьмём
![]() настолько малым, чтобы осуществление
события с вероятностью
настолько малым, чтобы осуществление
события с вероятностью
![]() можно было считать практически невозможным
в единичном опыте. Зная закон распределения
случайной величины
можно было считать практически невозможным
в единичном опыте. Зная закон распределения
случайной величины
![]() ,
найдем ее возможное значение
,
найдем ее возможное значение
![]() из уравнения
из уравнения
![]() .
По данной выборке вычислим значение
критерия согласия
.
По данной выборке вычислим значение
критерия согласия
![]() .
Если окажется, что
.
Если окажется, что
![]() ,
то это значит, что произошло практически
невероятное событие. Следовательно,
эксперимент опровергает нашу гипотезу,
и она отбрасывается.
При этом вероятность того, что мы
отбросили верную гипотезу, равна
.
Если
,
то это значит, что произошло практически
невероятное событие. Следовательно,
эксперимент опровергает нашу гипотезу,
и она отбрасывается.
При этом вероятность того, что мы
отбросили верную гипотезу, равна
.
Если
![]() ,
то гипотеза не противоречит эксперименту
и должна быть принята. Число
называется уровнем значимости критерия.
,
то гипотеза не противоречит эксперименту
и должна быть принята. Число
называется уровнем значимости критерия.
Колмогоров
нашел предельную функцию распределения
величины
![]() .
Эту функцию обычно обозначают
.
Эту функцию обычно обозначают
![]() :
:
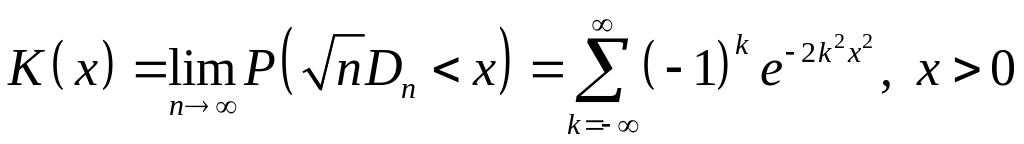
Формулой можно пользоваться для больших .
Чтобы
воспользоваться критерием согласия
Колмогорова, нужно построить графики
гипотетической и выборочной функций
распределения, по графикам найти
статистику
![]() и вычислить величину
и вычислить величину
![]() .
Найти вероятность события
.
Найти вероятность события
![]() по формуле
по формуле
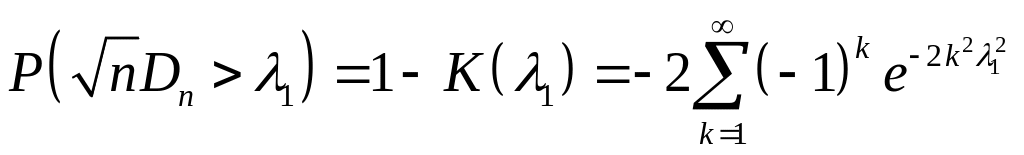
Если эта вероятность меньше , то гипотеза отвергается, если больше, то признается непротиворечащей эксперименту.
Предположим теперь, что, например, из физических соображений мы можем высказать гипотезу только о виде закона распределения, а параметры, входящие в него, неизвестны. Тогда критерий согласия Колмогорова не применим. В таких случаях часто используют критерий согласия Пирсона.
Всю
числовую ось разобьем на
![]() непересекающихся разрядов точками
непересекающихся разрядов точками
![]() .
Примем гипотезу о функции распределения.
Неизвестные
параметры, входящие в нее, заменим их
оценками. Таким
образом, гипотетическая функция
распределения
будет известна, и можно будет найти
вероятности
.
Примем гипотезу о функции распределения.
Неизвестные
параметры, входящие в нее, заменим их
оценками. Таким
образом, гипотетическая функция
распределения
будет известна, и можно будет найти
вероятности
![]() попадания случайной величины в
попадания случайной величины в
![]() -й
разряд. Возьмем статистику
-й
разряд. Возьмем статистику
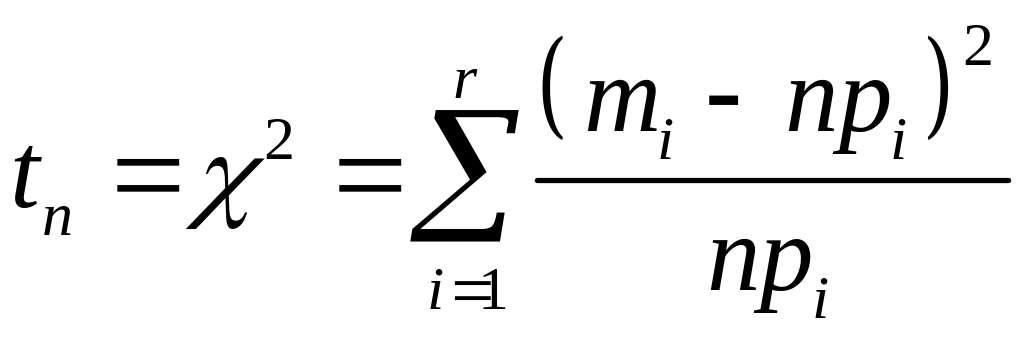
Здесь
–
объем выборки,
–
число разрядов,
![]() – число значений в
-м
разряде.
– число значений в
-м
разряде.
За
меру расхождения между гипотетической
и эмпирической
функциями распределения примем статистику
![]() ,
определенную формулой . Фишером
доказано, что предельным законом
распределения статистики
,
определенную формулой . Фишером
доказано, что предельным законом
распределения статистики
![]() является распределение
с
является распределение
с
![]() степенями свободы, если параметры
оценены по методу максимального
правдоподобия. Здесь
степенями свободы, если параметры
оценены по методу максимального
правдоподобия. Здесь
![]() –
число параметров, входящих в гипотетическую
функцию распределения. Доказано также,
что при объеме выборки
с достаточной точностью можно пользоваться
предельным законом распределения, если
–
число параметров, входящих в гипотетическую
функцию распределения. Доказано также,
что при объеме выборки
с достаточной точностью можно пользоваться
предельным законом распределения, если
![]() .
.
Схема
применения критерия Пирсона следующая.
По формуле вычисляют значение
статистики
![]() .
Вычисляют вероятность
.
Вычисляют вероятность
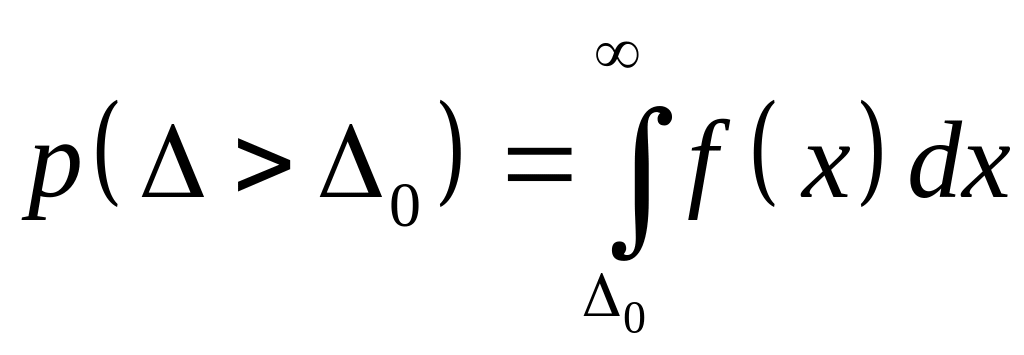
Здесь
определяется формулой
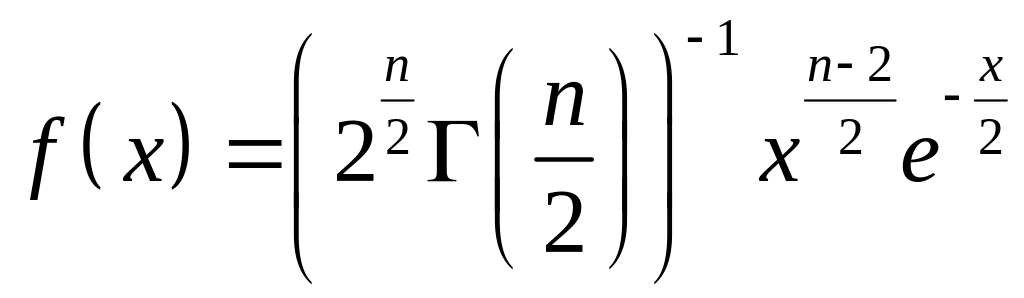 ,
а
следует заменить на
.
Если эта вероятность меньше уровня
значимости
,
то гипотезу следует отбросить.
,
а
следует заменить на
.
Если эта вероятность меньше уровня
значимости
,
то гипотезу следует отбросить.
Применение
критериев согласия иллюстрируют примеры
3.1-3.2. В начале генерируется (по методу
обратных функций) выборка значений
случайной величины, распределенной по
показательному закону с заданным
параметром
![]() .
Далее выборка группируется и находится
группированная функция распределения,
что необходимо для критерия Колмогорова.
В соответствии со схемой применения
критерия Колмогорова, задается
теоретическая функция распределения
,
и по этим значениям вычисляется статистика
.
Вычисляется вероятность по формуле и
сравнивается с уровнем значимости
.
.
Далее выборка группируется и находится
группированная функция распределения,
что необходимо для критерия Колмогорова.
В соответствии со схемой применения
критерия Колмогорова, задается
теоретическая функция распределения
,
и по этим значениям вычисляется статистика
.
Вычисляется вероятность по формуле и
сравнивается с уровнем значимости
.
В следующем разделе примеров применяется критерий Пирсона, Отметим, что, поскольку критерий Пирсона работает с плотностью распределения, для него может понадобиться другая группировка той же исходной выборки. Теоретическая плотность распределения может быть получена дифференцированием ранее введенной функции распределения. Теперь можно вычислить значение статистики и оценить вероятность , сравнивая ее с уровнем значимости .
