3.1. Окружность

Окружностью радиуса R с центром в точке М₀ называется множество всех точек М плоскости, удовлетворяющих условию М₀М=R.

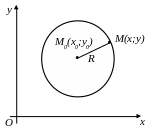
Рис. 7.

Пусть точка М₀ в прямоугольной системе координат xОy имеет координаты х₀, у₀, а точка М (х,у) – произвольная точка окружности. Тогда из условия М₀М=R получаем уравнение

.

Отсюда каноническое уравнение окружности примет вид:

(21)

Данному уравнению удовлетворяют координаты любой точки М (х,у) данной окружности и не удовлетворяют координаты никакой точки, не лежащей на окружности.

3.2. Эллипс

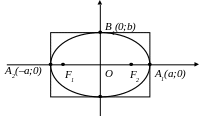
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, большая чем расстояние между фокусами.

Каноническое уравнение эллипса с центром в начале координат имеет вид:

(22)

y

x

В₂(0;–b)

Рис. 8.

Найдем точки пересечения эллипса с осями координат. Положив у=0, находим две точки А₁(а;0) и А₂ (-а;0), в которых ось Ох пересекает эллипс. Положив х=0, находим точки пересечения эллипса с осью Оу: В₁(0;b) и

В₂(0;-b). Отрезки А₁А₂ и В₁В₂ называются соответственно больной и малой осями эллипса. Числа a и b называются соответственно большой и малой полуосями эллипса.

Форма эллипса зависит от отношения . При b=a эллипс превращается в окружность, уравнение эллипса (22) принимает вид

.

В качестве характеристики формы эллипса чаще пользуются отношением – половины расстояния между фокусами к большой полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой (эпсилон):

Чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить , то эллипс превращается в окружность.

Если центр эллипса находится не в начале координат, а в произвольной точке О₁(х₀;у₀), то его каноническое уравнение эллипса будет иметь вид:

(23)

Чтобы построить такую фигуру, следует сначала сделать параллельный

перенос осей координат по правилу (см. 1.4.)

,

(24)

т огда в штрихованных координатах строится эллипс, как по уравнению (22).

Рис. 9.

3.3. Гипербола

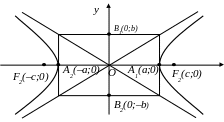
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

x

Рис.10.

Каноническое уравнение гиперболы с центром в начале координат имеет вид:

(25)

Здесь a – действительная полуось

b – мнимая полуось

Эксцентриситетом гиперболы называется отношение расстояния между фокусами к величине действительной оси гиперболы, обозначается : .

Чем меньше эксцентриситет гиперболы, тем меньше отношение ее полуосей, тем более вытянут ее основной прямоугольник.

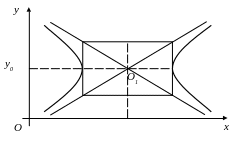
При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы, провести прямые, проходящие через противоположные вершины этого прямоугольника – асимптоты гиперболы и отметить ее вершины А₁ и А₂. Если центр гиперболы находится не в начале координат, а в произвольной точке О₁(х₀;у₀), то каноническое уравнение гиперболы будет иметь вид:

(27)

Чтобы построить гиперболу по уравнению (27), достаточно выполнить преобразование координат (4) и построить фигуру в штрихованных координатах.

x₀

Рис.11.
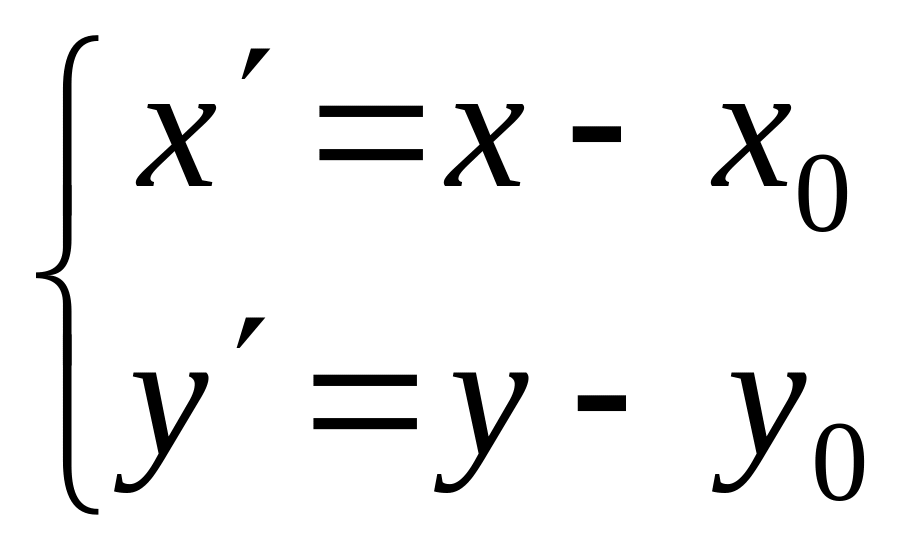