Теорема о сходимости метода бисекций

Пусть функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков Тогда метод бисекций сходится и справедлива оценка погрешности :

.

Например: Рассмотрим на отрезке [0;1] уравнение

f(x) = x - cosx = 0.

Найти приближенное значение корня уравнения t с помощью метода половинного деления.

Решение:

f(0) = -1 < 0; f(1 )= 1 - cos1 > 0;

f¢(x) = 1 + sinx > 0; при 0 £ x £ 1

11-кратное деление отрезка [0;1] пополам определяет корень с точностью e = (1/2)¹² < 0,00025. Искомый корень принадлежит отрезку: 0,73901 < t < 0,73926.

Метод хорд решения нелинейных уравнений

Пусть дано уравнение f(x)=0, где f(x) - непрерывная функция, имеющая в интервале (a, b) производные первого и второго порядка. Корень отделен и находится на отрезке [a, b], т.е. f(a)× f(b)<0.

Идея метода заключается в том, что на достаточно малом промежутке [a, b] дуга кривой y = f(x) заменяется стягивающий ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Оx.

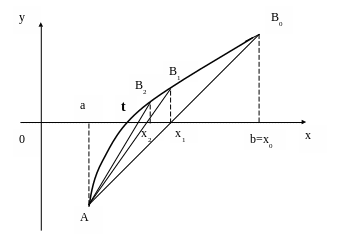
I. Случай, когда f¢ (x)× f² (x)>0

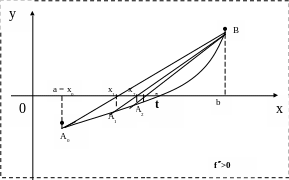
Уравнение хорды A₀B:

(из уравнения прямой, проходящей через две точки: )

Найдем значение x=x₁ для которого y=0.

или

(1)

Это формула метода хорд для первого шага.

Сейчас корень внутри отрезка [x₁,b]. Далее:

(2)

Здесь В – неподвижный конец хорды.

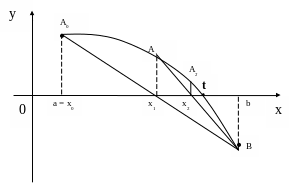
2. Случай, когда f¢ (x)× f² (x)<0

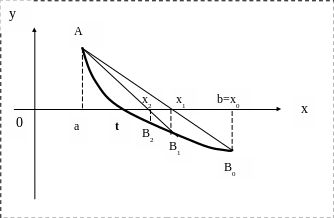
Хорда AB₀:

Найдем точку x₁ при y=0.

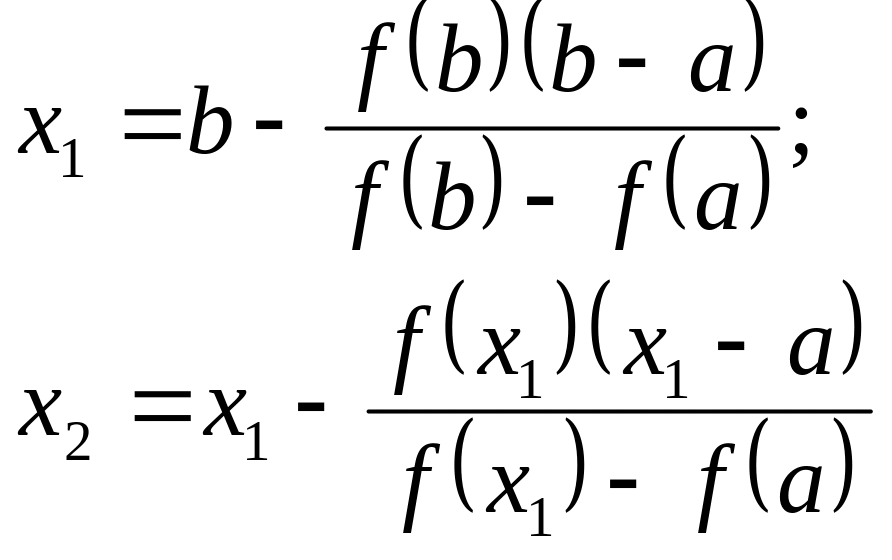(3)

Итак до (n+1)-го шага:

(4)

Здесь А - неподвижный конец хорды.

Правило выбора формул: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.

Оценка погрешности метода:

Эта формула справедлива лишь на достаточно малых отрезках. Ею можно пользоваться, если выполнено условие:

где

,

Метод Ньютона (метод касательных)

Пусть корень уравнения f(x)=0 отделен на отрезке [a, b], причем f¢ (x) и f² (x) непрерывны и сохраняют постоянные знаки на отрезке [a, b].

Геометрический смысл метода Ньютона состоит в том, что дуга кривой y=f(x) заменяется касательной к этой кривой.

1. Cлучай, когда . f(a)× f(b)<0 и f¢ (x)× f² (x)>0

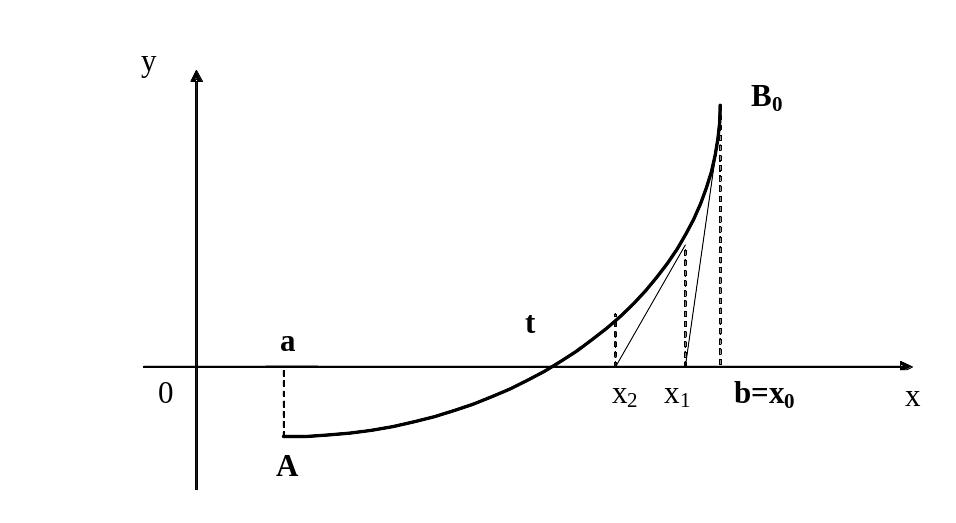
Уравнение касательной в точке B₀:

при y=0, x=x₁

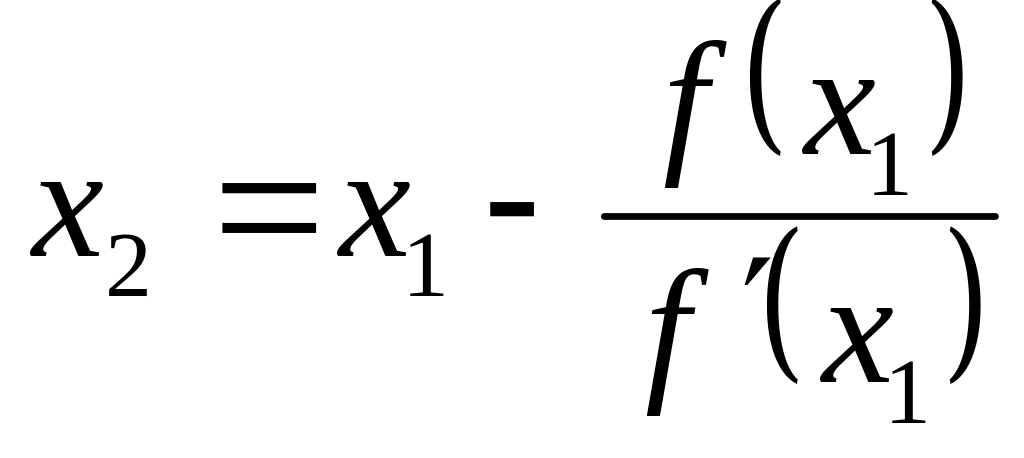
И наконец, формула метода Ньютона:

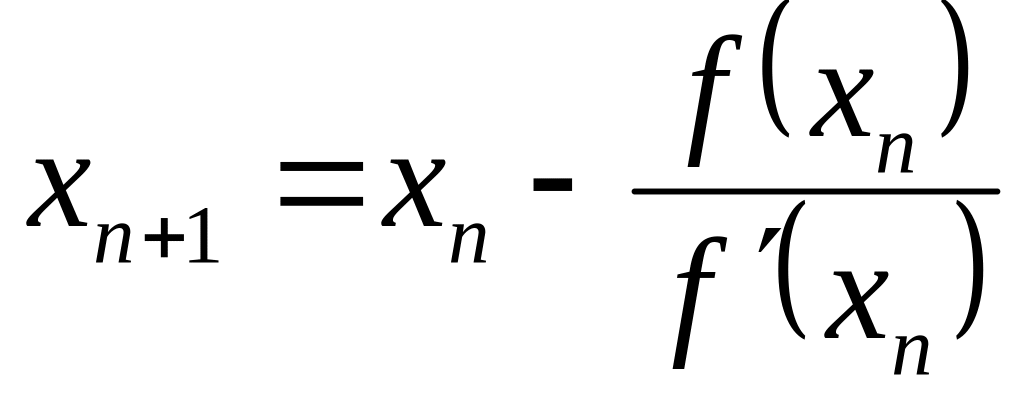
Определение: Корень t уравнения f(x)=0 называется простым, если , в противном случае корень называется кратным.

Целое число m называется кратностью корня t, если

Для k = 1,2,3,…, m-1 и .

Теорема о сходимости метода Ньютона

Пусть t - простой корень уравнения f(x)=0, и в некоторой окрестности этого корня функция f(x) дважды непрерывно дифференцируема.

Тогда найдется такая малая d-окрестность точки t, что при произвольном выборе начального приближения x₀ из этой малой окрестности (т.е. на (t-d,t+d) ) итерационная последовательность, порождаемая методом Ньютона, не выходит за пределы данной окрестности и справедлива оценка

, где n  0, C = d ^-1.

Как указано в теореме, метод Ньютона обладает локальной сходимостью, то есть областью его сходимости является малая окрестность корня t. Неудачный выбор начального приближения может дать расходящуюся итерационную последовательность.