Часть II. Методы решения нелинейных уравнений

Класс уравнений, для которых можно найти формулу решения, весьма узок. Уже для алгебраических уравнений пятой степени нет общей формулы, выражающей корни этого уравнения через его коэффициенты с помощью арифметических действий (доказано теоремой Абеля). Нет формул и для решения уравнений вида: , т.е. уравнений, включающих трансцендентные функции: тригонометрические, обратные тригонометрические и др.

Однако для решения практических задач не столь важно обладать формулой решения (аналитическое решение), важно уметь найти корни уравнения с заранее заданной точностью.

Иными словами, надо уметь решать такую задачу:

Дано уравнение f(x)=0, имеющее корни t₁, t₂,…, t_n и число e >0. Для каждого корня нужно найти его приближенное значение, т.е. число, отличающееся от данного корней этого уравнения меньше, чем на e по абсолютной величине. Число e является погрешностью (точностью) вычисления корня.

Процесс нахождения приближенных значений корней уравнения разбивается на два этапа:

1. отделение корней,

2. итерационное уточнение корней до заданной степени точности.

Отделение корней

Определение: Корень t уравнения f(x)=0 считается отделенным на отрезке [a,b], если на этом отрезке уравнение f(x)=0 не имеет других корней.

Два способа отделения корней.

1. графический метод: построением графиков вручную или с помощью компьютера;

2. аналитический метод: используя некоторые свойства функции, изучаемые в курсе математического анализа.

Теорема. Если функция непрерывна на отрезке [a,b] и принимает на концах отрезка значения разных знаков, т.е. f(a)×f(b)<0 а производная f¢(x) сохраняет постоянный знак внутри отрезка, то внутри отрезка существует корень уравнения f(x)=0 и притом единственный.

Итерационное уточнение корней

После того, как корень t отделен, на отрезке его локализации строится итерационная последовательность приближений x₁, x₂,…, x_n , … к точному значению корня. Существуют различные итерационные методы построения такой последовательности, которые мы и будем рассматривать.

Если построенная последовательность приближений сходится к точному значению корня, т.е.

,

то говорят, что итерационный метод сходится.

Метод половинного деления или бисекций

Дано уравнение f(x)=0, функция f(x) непрерывна на [a, b], принимает на его концах значения разных знаков и имеет на этом отрезке один корень (корень отделен). Предположим для определенности, что f(a)<0; f(b)>0. Возьмем среднюю точку b₁=(b + a)/a на [a, b], вычислим f(b₁). Если f(b₁)=0 - то корень найден, если нет, то рассмотрим два отрезка [a, b₁] и [b₁, b] и выберем тот, на концах которого функция имеет разные знаки.

.

т

Выбранный отрезок обозначим [a₁, b₁], f(a₁)<0, f(b₁)>0.

Повторим описанную процедуру. Неограниченное продолжение процесса дает последовательность отрезков [a, b], [a₁, b₁], [a₂, b₂],…. Эти отрезки вложены друг в друга – каждый последующий отрезок принадлежит предыдущим, причем f(a_n)<0, f(b_n)>0. Длины отрезков с возрастанием номера n стремятся к нулю:

,

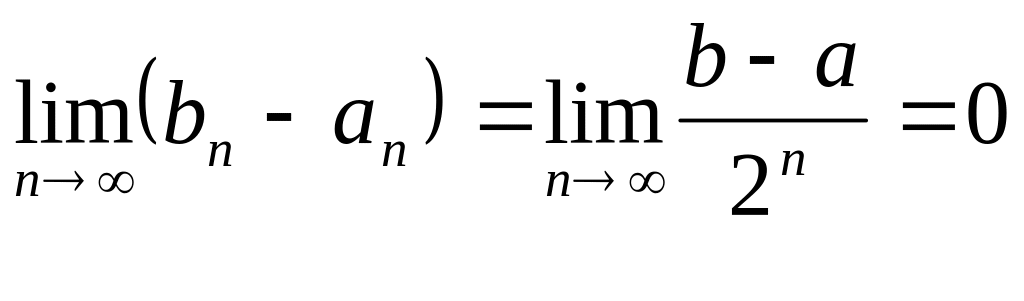следовательно, процесс сходится к корню уравнения.

Критерий окончания процесса вычислений: Пусть задана погрешность e, с которой необходимо найти корень. Если длина отрезка локализации корня [a_n, b_n] меньше 2e, то итерации прекращают и в качестве приближенного значения корня, найденного с заданной точностью принимают середину этого отрезка.