Общая формула для вычисления погрешностей

Если дана функция f(x, y, z), то , как следует из свойств приращений функции и первого дифференциала, абсолютная и относительная погрешности вычисления её значения можно приближенно оценить так:

СЕМИНАР 1

Тема: Элементы теории погрешностей

1. В результате измерения длины стола линейкой с сантиметровыми делениями установлено, что значение длины находится между делениями 63 и 64 см. Указать границы абсолютной и относительной погрешностей значения длины, если за наилучшее её приближение принять среднее значение 63,5 см.

2. В результате пятикратных измерений периода колебаний маятника студент получил результаты (в секундах): 4,8; 5,0; 4,9; 4,8; 5,0. Основываясь на этих измерениях, установить наилучшее приближение значения периода и границы абсолютной и относительной погрешностей.

3. Определить количество значащих цифр: 0,2409; 24,09; 100,700.

4. Округлить соответственно до двух, трёх и четырёх знаков после запятой следующие числа: 3,009982; 24,00551; 21,161728. Определить абсолютные и относительные (в процентах) погрешности полученных приближений.

5. Пусть a=2,91385 и a=0,0097. Какие цифры в числе a можно считать верными?

отв. (2, 9, 1)

6. Вычислить с помощью калькулятора 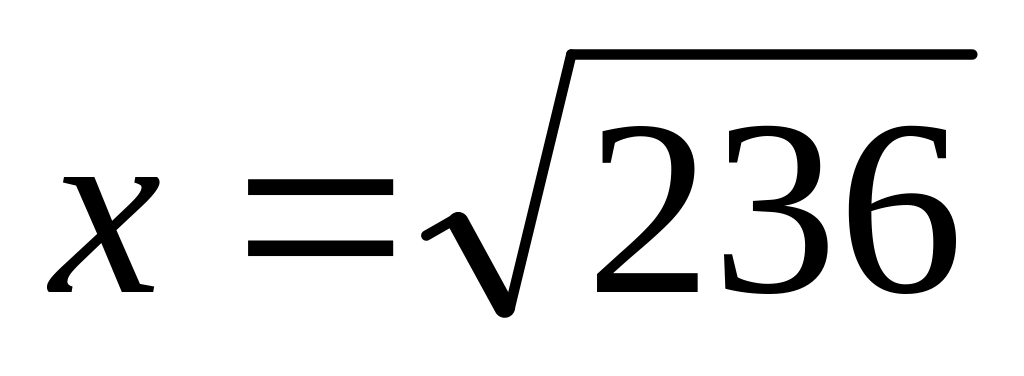(15,3623), округлить результат до десятых (x₁), найти абсолютную погрешность округления x₁. Назвать все верные цифры числа x₁.

7. Округлить сомнительные цифры числа a = 47,4530,024, оставив в нём верные знаки.

отв.(47,5)

8. Округлить сомнительные цифры числа a=46,38520,0031, оставив в нём верные знаки.

отв.(46,39)

9. Округлить сомнительные цифры приближенного числа a=3,2873, если относительная погрешность - _а=0,1%. Оставить в нём только верные знаки. ……….(3,29)

10. У приближенных чисел 36,7; 2,489; 31,010; 0,031 все цифры верны. Указать абсолютные и относительные погрешности этих чисел.

11. У приближенных чисел 0,310; 3,495; 24,3790 все цифры верны в строгом смысле. Округлить заданные числа до сотых и определить в округлённых значениях количество цифр, верных в строгом смысле.

12. Спортивная площадка имеет форму прямоугольника со сторонами: а = 10,02м, b = 5,01м. Найти её площадь S и относительную погрешность вычислений, если стороны измерены с точностью Δ=0,5 см.

13. Округлить сомнительные цифры числа a₁= 26,7245 ± 0,0026, оставив верные знаки. Определить абсолютную погрешность результата.

отв. 26,7±0,0271

Задачи с решениями

ЗАДАЧА 1. Определить предельную абсолютную погрешность приближенного

числа а = 5,213, если _a = 0,01%.

Решение: Запишем проценты в виде десятичной дроби и для определения абсолютной погрешности воспользуемся выше приведённой формулой, тогда

_a = a _a = 5,213 • 0,0001 = 0,00053.

(абсолютную погрешность всегда округляют с избытком).

ЗАДАЧА 2. Определить, какое равенство точнее: или ?

Решение: Для нахождения абсолютных погрешностей берем числа а и b с бớльшим числом десятичных знаков: 13/19  0,68421;  7,2111. Определяем абсолютные погрешности, округляя их с из­бытком:

D_a = | 0,68421—0,684 | < 0,00022; D_b = | 7,2111—7,21| < 0,0012.

Находим относительные, погрешности:

d_a = D_a / а = 0,00022 / 0,684 » 0,00033 = 0,033%;

d_b = D_b / b = 0,0012 / 7,21 » 0,00017 =0,017%.

Второе равенство является более точным, поскольку d_a > d_b.

ЗАДАЧА 3. Определить абсолютные погрешности приближенных чисел а = 96,387 и b = 9,32, если они содержат только верные цифры.

Решение: Так как для числа а = 96,387 последняя цифра 7, стоящая в разряде тысячных долей, является верной значащей цифрой, то D_a  0,5 • 0,001, т. е. D_a  0,0005. Тогда число а можно записать так: а = 96,387 ± 0,0005.

Последняя цифра приближенного числа b = 9,32 стоит в разряде сотых долей. Так как это число содержит верные цифры, то D_b  0,5• 0,01, т. е. D_b  0,005. Число b можно записать так: 9,32 ±0,005.

ЗАДАЧА 4. Округлить число А = 26,837 до трёх значащих цифр. Найти абсолютную и относительную погрешности округления.

Решение: Округляя число А = 26,837 до трех значащих цифр, получим а = 26,8, откуда D_a =| А - а | = | 26,837—26,8 | = 0,037 < 0,05, т. е. число а имеет три верные значащие цифры.

Относительная погрешность округления:

ЗАДАЧА 5. Округлить сомнительные цифры числа а₁ = 34,124 ( ± 0,021). Определить абсолютную погрешность результата.

Решение: Приближенное число a₁ имеет три верные цифры: 3, 4, 1, так как D_a = 0,021 < 0,05. Применяя правила округления, найдем приближенное значение а₂, сохранив десятые доли: а₂ = 34,1. Теперь получаем

D_a2 = D_a1 + D_окр = 0,021 + 0,024 = 0,045 < 0,05 = 0,510^-1.

Таким образом, все значащие цифры числа а₂ верные, т.е. е. а₂ = 34,1.

ЗАДАЧА 6. Округлить сомнительные цифры числа a₁ = 15,3654 ± 0,0018. Определить абсолютную погрешность результата.

Решение: Приближенное число a₁ = 15,3654 ± 0,0018 имеет четыре верные значащие цифры (1, 5, 3, 6), так как D_a1 = 0,0018 < 0,005 = 0,510^-2. При округлении до четырех значащих цифр получим а₂ = 15,37 и D_a2 = D_a1 + D_окр = 0,0018+0,0046 = 0,0064. Очевидно, что

0,005 < 0,0064 < 0,05.

Следовательно, число 15,37 ± 0,0064 имеет четыре верные цифры.

ЗАДАЧА 7. Найти произведение приближенных чисел х = 3,6 и y = 84,507, все цифры которых верны.

Решение: В первом числе две верные значащие цифры, а во втором - пять. Поэтому второе число округляем до трех значащих цифр. После округления имеем х= 3,6; y = 84,5.

Отсюда xy = 3,6 • 84,5 = 304,20  3,0 •10².

В результате оставлены две значащие цифры, т. е. столько, сколько их имел сомножитель с наименьшим количеством верных значащих цифр.

ЗАДАЧА 8. Определить произведение и приближенных чисел x = 12,4 и y= 65,54 и число верных знаков в нём, если все написанные цифры сомножителей верны.

Решение: В первом из чисел три верные значащие цифры, во втором - четыре; можно перемножить числа без предварительного округления: u = 12,4 • 65,54 = 812,696. Следует оставить три значащие цифры, так как наименее точный из сомножителей имеет столько же верных значащих цифр. Таким образом, и = 813.

Подсчитаем погрешность:

Тогда D_u = 813  0,0048  4.

Значит, произведение u имеет два верных знака (8;1) и его следует записать так:

u = 813  4.

ЗАДАЧА 9. Задано число 3572,121 ±0,02. Определить его верные значащие цифры.

Решение: Согласно определению

D_а = 0,02 > ½ 10^-3 .= 0,0005,

D_a = 0,02 > ½ 10^-2 = 0,005,

D_a = 0,02< ½ 10^-1 = 0,05.

Итак, в числе 3572,121 ±0,02 только первые пять цифр: 3,5,7,2,1 — верные значащие. Поэтому ответ имеет вид: 3572,1 ± 0,02.

ЗАДАЧА 10. Вычислить при n = 3,0567 ±0,0001, т = 5,72 ±0,02:

A =(n — l)(m + n)/(m — n)²

и определить погрешности результата.

Решение: Так как единица – число точное, (n - 1) = 2,0567 ±0,0001; с учетом теоремы 1 об абсолютной погрешности алгебраической суммы: (т + п) = 8,7767 ±0,0201, (т – п) = 2,6633 ± 0,0201.

Тогда

Последний результат получен с помощью правила подсчета цифр (число т содержит три значащие цифры) и последовательного округления.

Далее вычисляем относительную погрешность результата согласно теоремам 2 ÷ 4:

Абсолютная погрешность: ∆_а = 2,54 • 0,0174  0,0442

Следовательно, приближенное значение: а = 2,54 ± 0,0442.

Затем вычисляем верные значащие цифры результата:

0,0442 > ½ 10^-2 = 0,005,

0,0442 < ½ 10^-1 = 0,05.

Итак, цифры 2, 5 — верные значащие цифры, что позволяет записать ответ: А = 2,5 ± 0,0442, _а = 0,0174.