6.5. Статистические характеристики огибающей и фазы случайных процессов

Синфазную и квадратурную составляющие можно представить в виде:

Вычислим корреляционную функцию :

Подставим выражения для и , получим:

Аналогично

Взаимная корреляционная функция

.

Дисперсии синфазной и квадратурной составляющих равны дисперсии исходного процесса:

Для того чтобы найти двумерную плотность вероятности огибающей и фазы случайного процесса , воспользуемся двумерной ПРВ квадратурной и синфазной составляющих. Будем полагать, что исходный процесс - нормальный, тогда и - также нормальны и независимы. Их совместная ПРВ в этом случае равна произведению одномерных плотностей вероятности:

Для того чтобы найти искомую ПРВ , совершим замену:

Якобиан преобразования (см. выражение(6.1))

Учитывая, что A²+B²=U², получаем искомую двухмерную плотность

Проинтегрировав по U, получив ПРВ начальной фазы:

Таким образом, распределение случайной фазы равномерное на отрезке [0, 2 ].

Поскольку в выражении для нет зависимости от угла, то

Плотность распределения огибающей нормального случайного процесса носит название закона Рэлея (рис. 6.6).

Матожидание

Рис. 6.6. Плотность распределения вероя- тности огибающей нормального случайного процесса

и дисперсия

Найдем совместную ПРВ огибающей и нормальной фазы для нормального случайного процесса в два момента времени t и . Пусть x₁=A(t₁), x₂=A(t₂), y₁=B(t₁), y₂=B(t₂) и f₄(x₁), x₂ y₁, y₂ - совместное распределение и в два момента времени t и :

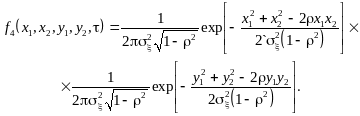(6.2)

Полагаем, что случайные величины х и y (как синфазная и квадратурная составляющая) независимы, а функции корреляции для х и y равны:

С помощью замены перейдем к огибающей и начальной фазе:

Якобиан преобразования

После преобразований, получим:

Для того чтобы найти двумерную ПРВ огибающей, проинтегрируем четырехмерную ПРВ по фазам и :

Учитывая, что модифицированная функция Бесселя нулевого порядка

получаем:

Определив двухмерную плотность распределения огибающей, можно легко найти корреляционную функцию огибающей:

Матожидания огибающей уже вычислено, поэтому его квадрат равен , среднее значение произведения

Раскладываем в ряд по многочленам Лагерра и после интегрирования получаем:

(6.3)

Разделив выражение (6.3) на дисперсию, получим нормированную корреляционную функцию

6.6. Статистические характеристики огибающей суммы гармонического сигнала и узкополосного шума

Пусть на входе радиотехнического устройства присутствует сумма узкополосного нормального шума и детерминированного гармонического сигнала :

Очевидно, что

Плотность распределения вероятностей синфазной и квадратурной составляющих

Переходя к новым переменным, получаем (якобиан преобразования равен U):

(6.4)

Чтобы получить одномерную ПРВ огибающей U, надо проинтегрировать выражение для по фазе:

(6.5)

Рис. 6.7. Плотность распределения вероятности огибающей суммы гармонического сигнала и нормального шума

Выражение (6.5) носит название закона Райса (рис. 6.7).

При отсутствии детерминированного гармонического сигнала, т.е. при из выражения (6.5) получим закон Рэлея. При больших значениях ПРВ огибающей стремится к нормальной:

с дисперсией, равной , и матожиданием .

Одномерное распределение фазы можно получить проинтегрировав выражение (6.4) по U:

После интегрирования получим:

Рис. 6.8. Плотность распределения вероятности фазы суммы гармонического сигнала и нормального узкополосного шума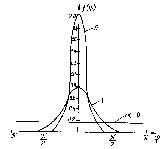

,

где - интеграл вероятности. Плотность вероятности фазы показана на рис. 6.8.

При больших соотношениях сигнал/шум - распределение фаз стремится к нормальному с дисперсией :

при >>1.

Несколько сложнее получить соотношение для мгновенной частоты. Для этого необходимо получить для суммы гармонического сигнала и шума выражение, аналогичное формуле (6.2). Затем, вспомнив, что частота - это производная от фазы, можно получить четырехмерную плотность для огибающей, фазы и их производных:

здесь

Одномерная ПРВ производной от фазы

После интегрирования формула приобретет вид:

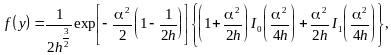(6.6)

где

Рис. 6.9. Плотность распределения вероятности мгновенной частоты суммы гармонического сигнала и нормального узкополосного шума

Здесь - мгновенная частота.

На рис. 6.9 показана зависимость (6.6) для разных отношений сигнал/шум.

При большом сигнале ПРВ стремится к нормальной с дисперсией .