
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
Фундаментальные последовательности в . Критерий сходимости Коши
Последовательность
точек пространства
называется фундаментальной (или
сходящейся в себе, или последовательностью
Коши), если для любого
существует такой номер
,
что
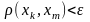
Критерий:Для того, чтобы последовательность точек пространства была сходящейся необходимо и достаточно, чтобы она была фундаментальной.
Понятие внутренней точки множества и его внутренности.. Определение и свойства открытых множеств в . Примеры открытых множеств.
Точка множества называется внутренней точкой этого множества, если она принадлежит ему вместе с некоторой своей окрестностью.
Совокупность всех
внутренних точек множества
обозначается
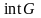 и называется внутренностью множества
.
и называется внутренностью множества
.
Множество называется открытым, если каждая его точка является внутренней, т.е. если =
Пример 1. Во
множестве вещественных чисел
,
которое мы естественно отождествляем
с пространством
 ,
-окрестностью
точки
является интервал
,
-окрестностью
точки
является интервал
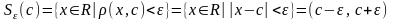 (здесь
следует иметь в виду, что в
(здесь
следует иметь в виду, что в
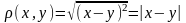 ).
).
Так как любой
конечный или бесконечный интервал
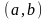 вместе с каждой своей точкой
при некотором
содержит и интервал
вместе с каждой своей точкой
при некотором
содержит и интервал
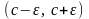 ,
то всякий интервал
является открытым множеством□
,
то всякий интервал
является открытым множеством□
Понятие точки сгущения множества в пространстве . Определение замкнутого множества . Критерий замкнутости в терминах предела.
Точка
называется
точкой сгущения или, также, предельной
точкой множества
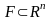 ,
если в любой ее проколотой окрестности
,
если в любой ее проколотой окрестности
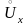 имеется хотя бы одна точка множества
,
т.е. если
имеется хотя бы одна точка множества
,
т.е. если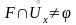 .
.
Множество называется замкнутым, если оно содержит все свои точки сгущения.
Критерий замкнутости Для того чтобы множество было замкнутым необходимо и достаточно, чтобы оно содержало предел любой своей сходящейся последовательности.
Связь между открытыми и замкнутыми множествами и свойства замкнутых множеств в . Примеры замкнутых множеств.
Теорема 4. Множество
является открытым тогда и только тогда,
когда его дополнение
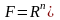 является замкнутым.
является замкнутым.
Д о к а з а т е л ь с т в о. Необходимость. Пусть множество открыто. Тогда ни одна его точка не может быть точкой сгущения множества (ибо всякая такая точка имеет окрестность целиком лежащую в и, значит, непересекающуюся с ). Таким образом, множество содержит все свои точки сгущения, т.е. является замкнутым
Достаточность. Пусть множество замкнуто. Тогда ни одна точка множества не является точкой сгущения множества . Поэтому каждая точка множества имеет целиком содержащуюся в нем свою окрестность. Следовательно, множество открыто □
58. Понятие функции нескольких переменных
Пусть
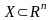 .
Тогда отображение (функция)
.
Тогда отображение (функция)
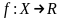 называется функцией
переменных, заданной на множестве
,
при этом множество
,
как и в случае произвольного отображения,
называется областью определения функции
.
называется функцией
переменных, заданной на множестве
,
при этом множество
,
как и в случае произвольного отображения,
называется областью определения функции
.
Определение предела функции нескольких переменных в смысле Коши и его геометрическая форма.
(определение
предела по Коши).
Пусть функция
определена на множестве
и
– точка сгущения этого множества. Число
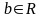 называется пределом функции
при
называется пределом функции
при
 ,
или пределом функции
,
или пределом функции
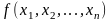 при
при
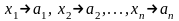 ,
или также пределом функции
в
точке
,
или также пределом функции
в
точке
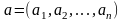 ,
если для любого
существует такое
,
что для любого
,
если для любого
существует такое
,
что для любого
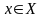 ,
удовлетворяющего неравенствам: (1)
,
удовлетворяющего неравенствам: (1)
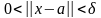
|
имеет место
неравенство(2)
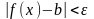
|
|
Определение предела функции нескольких переменных в смысле Гейне.
(определение
предела по Гейне)
Пусть функция
определена на множестве
и
– точка сгущения этого множества. Число
называется пределом функции
при
или, также, пределом функции
в точке
,
если для любой последовательности
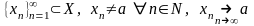 ,
последовательность
,
последовательность
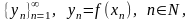 сходится и
сходится и
|
|
Определение
непрерывности функции нескольких
переменных на языке
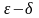 и его геометрическая форма.
и его геометрическая форма.
(определение
непрерывности
на языке «
»).
Функция
,
,
называется непрерывной в точке
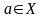 ,
если для любого
существует такое
,
что для любого
,
удовлетворяющего неравенству
,
если для любого
существует такое
,
что для любого
,
удовлетворяющего неравенству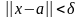 ,
,
справедливо
неравенство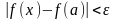 .
.
Определение непрерывности функции нескольких переменных на языке последовательностей.
Функция
,
,
называется непрерывной в точке
,
если для любой последовательности точек
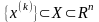 ,
сходящейся к точке
(
,
сходящейся к точке
(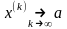 ),
числовая последовательность
),
числовая последовательность
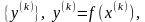 сходится к точке
сходится к точке
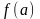 ,
т.е.
,
т.е.
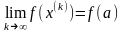 .
.
Теорема о непрерывности сложной функции.
Теорема
1
(о непрерывности
сложной функции).
Пусть функции
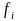 ,
,
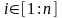 ,
определены на множестве
,
определены на множестве
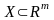 и непрерывны в точке
и непрерывны в точке
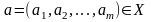 ,
а функция
определена на множестве
,
а функция
определена на множестве
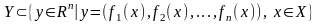 ,
,
и непрерывна в
точке
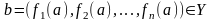 .
Тогда сложная функция
.
Тогда сложная функция
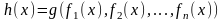 ,
,
,
,
непрерывна в точке .
Понятия непрерывной и равномерно непрерывной функции на множестве. Понятие компактного множества в пространстве .
Функция
,
,
называется непрерывной на множестве
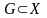 ,
если она непрерывна в каждой точке этого
множества.
,
если она непрерывна в каждой точке этого
множества.
Функция
,
,
называется равномерно непрерывной на
множестве
,
если
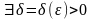 такое, что
такое, что
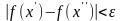
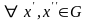 ,
,
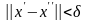 .
.
Множество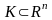 называется
компактным или также компактом, если
называется
компактным или также компактом, если
оно замкнуто и ограничено.
Теоремы Кантора и Вейерштрасса о непрерывной функции на компакте
Теорема кантора
Всякая
непрерывная
на компакте
функция
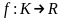 является на нем равномерно непрерывной.
является на нем равномерно непрерывной.
(первая теорема Вейерштрасса о непрерывных на компакте функциях).
Всякая непрерывная на компакте функция – ограничена на нем.
(вторая теорема Вейерштрасса о непрерывных на компакте функциях).
Всякая непрерывная на компакте функция достигает на нем своих точной верхней и точной нижней граней.
Понятия дифференцируемой функции нескольких переменных и ее дифференциала. Непрерывность и дифференцируемость.
Пусть
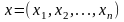 –
внутренняя точка множества
–
внутренняя точка множества
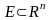 .
Функция
.
Функция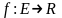 называется дифференцируемой в точке
Х, если существует такая линейная функция
называется дифференцируемой в точке
Х, если существует такая линейная функция
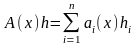 ,
,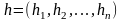
() переменных
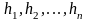 ,
что
,
что
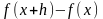
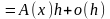 (здесь
(здесь
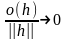 при
при
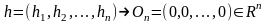
при этом линейная
функция
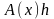 называется дифференциалом функции
в точке Х и обозначается
называется дифференциалом функции
в точке Х и обозначается
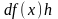 или,
короче,
или,
короче,
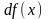 Теорема
1. Если функция
Теорема
1. Если функция
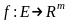 дифференцируема в точке
дифференцируема в точке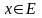 ,
то она и непрерывна в этой точке.
,
то она и непрерывна в этой точке.
Доказательство. Достаточно заметить, что в силу (2)
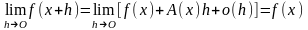 □
□
Понятие частной производной функции нескольких переменных.
Пусть – некоторая функция переменных и – внутренняя точка множества . Если существует предел
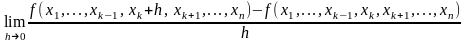 ,то
он называется частной производной
функции
в точке
по
-ой
переменной.
,то
он называется частной производной
функции
в точке
по
-ой
переменной.
Теорема о существовании частных производных
Теорема 2.
Дифференцируемая
в точке
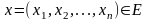 функция
имеет в этой точке конечные частные
производные
функция
имеет в этой точке конечные частные
производные
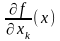 по всем переменным,
по всем переменным,
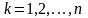 ,
при этом
,
при этом
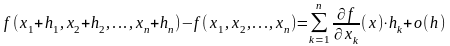 (
,
(2)
(
,
(2)
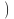 ).и
следовательно дифференциал функции
имеет вид
).и
следовательно дифференциал функции
имеет вид
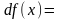
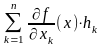 Д
о к а з а т е л ь с т в о. Так как функция
дифференцируема в точке
Д
о к а з а т е л ь с т в о. Так как функция
дифференцируема в точке
,
то имеет место равенство (1), где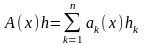 ,
,
и, следовательно, равенство (1) можно записать в виде
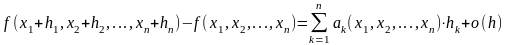 (
при
(
при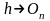 (3)
В частности для любого вектора
(3)
В частности для любого вектора
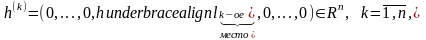 последнее равенство принимает вид:
последнее равенство принимает вид:
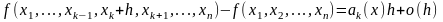
(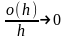 при
при
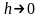 ),Отсюда
следует, что для любого
существует конечный предел
),Отсюда
следует, что для любого
существует конечный предел
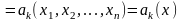 ,
,
который по
определению 3, в то же время, равен частной
производной
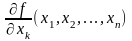 .
Поэтому равенство (3) можно записать в
виде (2) □
.
Поэтому равенство (3) можно записать в
виде (2) □
Достаточное
условие дифференцируемости функции
нескольких переменных.
(достаточное
условие
дифференцируемости).
Пусть все частные производные
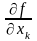 ,
,
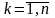 ,
функции
,
существуют
и непрерывны в точке
.
Тогда функция
дифференцируема в точке
.
,
функции
,
существуют
и непрерывны в точке
.
Тогда функция
дифференцируема в точке
.
Д о к а з а т е л ь с т в о. В силу теоремы Лагранжа для функций одной переменной и непрерывности частных производных имеем:
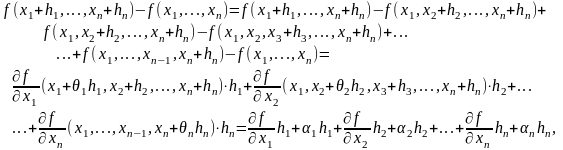 где
где
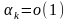 при
,
.
Таким образом,
при
,
.
Таким образом,
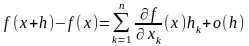 □
□

 геом
форма
геом
форма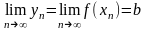 .
.