
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
Определение 1.
Пусть функция
(
)
раз дифференцируема в точке
.
Тогда однородный многочлен степени
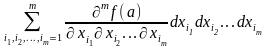 от
переменных
от
переменных
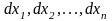 называется дифференциалом
-го
порядка функции
в точке
.Дифференциал
-го
порядка функции
в точке
обозначается
называется дифференциалом
-го
порядка функции
в точке
.Дифференциал
-го
порядка функции
в точке
обозначается
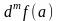 .
Таким образом,
.
Таким образом,
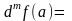 Замечание
1. Здесь и
выше в определении 1
Замечание
1. Здесь и
выше в определении 1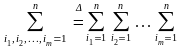 и,
следовательно, необходимо иметь в виду,
что под знаком
-кратной
суммы в определении 1 и формуле (1)
некоторые из чисел
и,
следовательно, необходимо иметь в виду,
что под знаком
-кратной
суммы в определении 1 и формуле (1)
некоторые из чисел
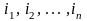 и даже все они могут быть равными друг
другу.
и даже все они могут быть равными друг
другу.
Замечание 2.
При
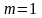 формула (1) принимает вид:
формула (1) принимает вид: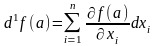 .Следовательно
дифференциал первого порядка функции
в точке
это – просто ее дифференциал в этой
точке.Замечание
3. При
.Следовательно
дифференциал первого порядка функции
в точке
это – просто ее дифференциал в этой
точке.Замечание
3. При
 формула (1) имеет вид
формула (1) имеет вид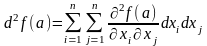 при
этом здесь предполагается, что функция
дважды дифференцируема в точке
.
Таким образом, если первый дифференциал
функции
представляет собой линейную функцию
переменных
при
этом здесь предполагается, что функция
дважды дифференцируема в точке
.
Таким образом, если первый дифференциал
функции
представляет собой линейную функцию
переменных
 ,
,
то второй ее дифференциал представляет
собой квадратичную форму от тех же
переменных.
,
,
то второй ее дифференциал представляет
собой квадратичную форму от тех же
переменных.
79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
Если функция
определена в некоторой окрестности
 точки
и имеет в этой точке всевозможные частные
производные до порядка
включительно, то ее можно представить
в виде
точки
и имеет в этой точке всевозможные частные
производные до порядка
включительно, то ее можно представить
в виде
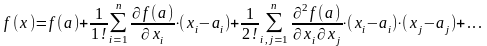
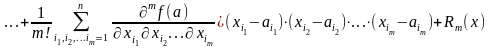 ,
,
Эта формула
называется формулой Тейлора функции
переменных, при этом функция
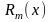 ,
стоящая в правой ее части, называется
остаточным членом формулы Тейлора.Замечание
1. Учитывая
определение дифференциала порядка
функции
и то, что дифференциал любого порядка
есть функция дифференциалов независимых
переменных, формулу Тейлора (7) можно
записать следующим образом:
,
стоящая в правой ее части, называется
остаточным членом формулы Тейлора.Замечание
1. Учитывая
определение дифференциала порядка
функции
и то, что дифференциал любого порядка
есть функция дифференциалов независимых
переменных, формулу Тейлора (7) можно
записать следующим образом:
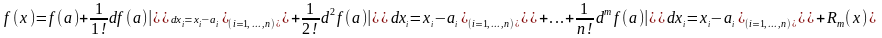 Теорема
1. Пусть
Теорема
1. Пусть
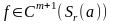 ,
т.е. пусть функция имеет в окрестности
точки
всевозможные
частные производные до порядка
,
т.е. пусть функция имеет в окрестности
точки
всевозможные
частные производные до порядка
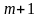 включительно и все они непрерывны в
этой окрестности. Тогда при любом
включительно и все они непрерывны в
этой окрестности. Тогда при любом
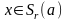 для функции
справедлива формула Тейлора (1) с
остаточным членом в форме Пеано:
для функции
справедлива формула Тейлора (1) с
остаточным членом в форме Пеано: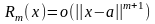
Понятие
локального экстремума функции
нескольких переменных. Необходимое
условие локального экстремума
Определение
1. Пусть
функция
определена на множестве
.
Точка
называется точкой локального максимума
функции
,
если существует такое
|
|
при этом если
последнее неравенство является строгим
для всех указанных здесь
,
то точка
называется точкой строго локального
максимума функции
.Аналогично,
определяются понятия точек локального
минимума и строгого локального минимума
функции
(для
этого в (1) неравенство
или, соответственно, < заменяется на
неравенство
или соотв. на > ). Если точка
является точкой локального максимума
или точкой локального минимума, то она
называется также точкой локального
экстремума. Аналогично вводится понятие
точки строгого локального экстремума.
Замечание
1. Если
– внутренняя точка множества
,
то в определении 1, достаточно требовать,
чтобы соответствующее неравенство
выполнялось для всех
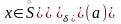 ,
так как
всегда может быть выбрано так, что
,
так как
всегда может быть выбрано так, что
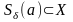 .Теорема
1. Пусть
функция
определена в некоторой окрестности
точки
и имеет в этой точке частные производные
по всем переменным. Тогда, если точка
– точка локального экстремума функции
,
то все ее частные производные в этой
точке равны нулю:
.Теорема
1. Пусть
функция
определена в некоторой окрестности
точки
и имеет в этой точке частные производные
по всем переменным. Тогда, если точка
– точка локального экстремума функции
,
то все ее частные производные в этой
точке равны нулю: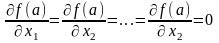 ,
,
т.е.
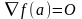 .Д
о к а з а т е л ь с т в о.
Выберем произвольное
и рассмотрим следующую функцию скалярного
аргумента
.Д
о к а з а т е л ь с т в о.
Выберем произвольное
и рассмотрим следующую функцию скалярного
аргумента
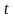 :
: (
(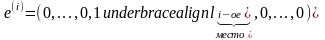 ).Так
как функция
определена в некоторой окрестности
точки
и имеет в этой точке частную производную
по
–ой
переменной, то функция
).Так
как функция
определена в некоторой окрестности
точки
и имеет в этой точке частную производную
по
–ой
переменной, то функция
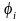 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки
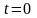 и имеет в ней производную
и имеет в ней производную
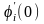 ,
при этом по определению частной
производной по
–ой
переменной
,
при этом по определению частной
производной по
–ой
переменной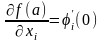 .
.
Более того, так
как
– точка локального экстремума функции
,
то, очевидно, точка
– точка локального экстремума функции
.
Тогда по теореме Ферма
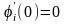 ,
т.е.
,
т.е.
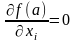 .
В силу произвольности выбранного
это и означает, что
.
В силу произвольности выбранного
это и означает, что

Достаточное условие локального экстремума функции нескольких переменных Определение 2. Пусть функция определена в окрестности точки и имеет в этой точке частные производные первого порядка по всем переменным. Тогда если , то точка называется стационарной точкой функции или, также, точкой подозрительной на экстремум. Теорема 2. Пусть – стационарная точка функции и функция дважды непрерывно дифференцируема в окрестности точки .Тогда 1) если второй дифференциал функции в точке является положительно определенной квадратичной формой, то точка – точка строго локального минимума функции , а если он представляет собой отрицательно определенную квадратичную форму, то точка – точка строгого локального максимума функции ;

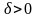 ,
что
,
что
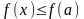
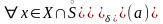 ,
,