
- •Формула интегрирования по частям для неопределенного интеграла.
- •Основные свойства определенного интеграла Римана: интегрируемость сужения, аддитивное свойство, линейные свойства, интегрируемость произведения.
- •Число e как сумма ряда.
- •Понятие знакочередующегося ряда. Признак Лейбница. Исследование ряда
- •Понятия абсолютно и условно сходящегося числового ряда. Теорема о сходимости абсолютно сходящегося ряда.
- •Основные теоремы о степенных рядах (о непрерывности суммы степенного ряда, о почленном дифференцировании и почленном интегрировании степенного ряда)
- •Разложение функций в степенные ряды (определение).
- •Определения несобственных интегралов 1-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 1-го рода.
- •Определения несобственных интегралов 2-го рода (с различными видами особенностей), сходящиеся и расходящиеся несобственные интегралы 2-го рода.
- •Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
- •Критерий сходимости несобственного интеграла от неотрицательной функции.
- •Интегральный признак сходимости числового ряда.
- •Скалярное произведение и евклидова норма в (определения). Неравенство Коши-Буняковского.
- •53. Координатные последовательности последовательности точек в . Критерий сходимости последовательности в в терминах координатных последовательностей.
- •58. Понятие функции нескольких переменных
- •Понятие градиента и его арифметические свойства
- •4°. (Здесь предполагается, что g ¹ 0 в соответствующей точке).
- •Определение дифференциалов высших порядков. Иллюстрация определения на примере дифференциалов 1-го и 2-го порядков.
- •79. Формула Тейлора для функции нескольких переменных (включая формулировку теоремы о разложимости функции по формуле Тейлора с остаточным членом в форме Пеано)
- •2) Если же второй дифференциал функции в точке является знакопеременной квадратичной формой, то точка не является точкой локального экстремума функции .
Теорема о замене переменной и формула интегрирования по частям для несобственных интегралов.
5о.
Теорема о
замене переменной.
Пусть функция
непрерывна на бесконечном или
полубесконечном промежутке
,
а функция
1) либо непрерывно дифференцируема на
конечном или бесконечном промежутке
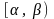 ,
возрастает на нем,
,
возрастает на нем,
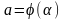 и
и
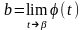 ,
2) либо непрерывно дифференцируема на
конечном или полубесконечном промежутвке
,
2) либо непрерывно дифференцируема на
конечном или полубесконечном промежутвке
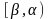 ,
убывает на нем,
,
убывает на нем,
 и
и
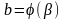 .
Тогда интегралы
.
Тогда интегралы
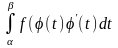 и
(8)
сходятся или нет одновременно и если
сходятся, то имеет место формула
и
(8)
сходятся или нет одновременно и если
сходятся, то имеет место формула
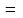 (формула замены переменной в несобственном
интеграле) (9). 6о.
Формула
интегрирования по частям.
Пусть функции
и
непрерывно дифференцируемы на промежутке
и существует (конечный) предел
(формула замены переменной в несобственном
интеграле) (9). 6о.
Формула
интегрирования по частям.
Пусть функции
и
непрерывно дифференцируемы на промежутке
и существует (конечный) предел
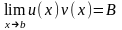 . (12)
Тогда из сходимости одного из интегралов
. (12)
Тогда из сходимости одного из интегралов
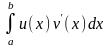 и
и
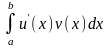 (13)
вытекает сходимость другого, и если они
сходятся, то имеет место формула :
(13)
вытекает сходимость другого, и если они
сходятся, то имеет место формула :
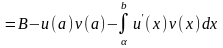 (формула
интегрирования по частям)(14) Д
о к а з а т е л ь с т в о.
При сделанных предположениях для любого
,
(формула
интегрирования по частям)(14) Д
о к а з а т е л ь с т в о.
При сделанных предположениях для любого
,
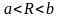 имеет место формула интегрирования по
частям для определенного интеграла
(15) С учетом того, что существует конечный
предел (12), отсюда, очевидно следует, что
интегралы (13) сходятся или нет одновременно,
а если сходятся то имеет место формула
(14), которая получается в результате
перехода к пределу при
имеет место формула интегрирования по
частям для определенного интеграла
(15) С учетом того, что существует конечный
предел (12), отсюда, очевидно следует, что
интегралы (13) сходятся или нет одновременно,
а если сходятся то имеет место формула
(14), которая получается в результате
перехода к пределу при
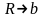 в формуле (15) □ Замечание
1. Обычно формулу (14) записывают также
как и в случае обычного –собственного
интеграла:
в формуле (15) □ Замечание
1. Обычно формулу (14) записывают также
как и в случае обычного –собственного
интеграла:
 ,где
,где
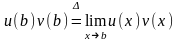 .
Ее записывают также и в виде
.
Ее записывают также и в виде
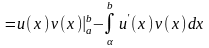 .
.
Критерий сходимости
Коши и теорема сравнения для несобственных
интегралов. Абсолютно и условно сходящиеся
несобственные интегралы.
Пусть функция
определена на полуоси
и интегрируема по Риману на любом отрезке
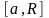 ,
,
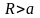 .
Теорема 1 (Критерий Коши). Несобственный
интеграл
(1) сходится тогда и только тогда, когда
для любого
найдется такое
.
Теорема 1 (Критерий Коши). Несобственный
интеграл
(1) сходится тогда и только тогда, когда
для любого
найдется такое
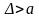 ,
что для любых
,
что для любых
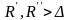 имеет место неравенство
имеет место неравенство
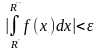 .(2)
Д о к а з а т
е л ь с т в о.
Сходимость интеграла (1) означает
существование конечного предела функции
.(2)
Д о к а з а т
е л ь с т в о.
Сходимость интеграла (1) означает
существование конечного предела функции
 (3)
при
(3)
при
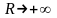 .
В силу критерия Коши для существования
предела
.
В силу критерия Коши для существования
предела
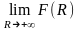 необходимо и достаточно, чтобы для
любого
существовало такое
,
что для любых
выполнялось неравенство
необходимо и достаточно, чтобы для
любого
существовало такое
,
что для любых
выполнялось неравенство
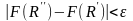 .
Остается заметить, что (3) ~ (2). Пусть
наряду с функцией
на полуоси
определена функция
,
которая, как и функция
, интегрируема по Риману на любом отрезке
,
.
Теорема 2
(признак
сравнения). Пусть
.
Остается заметить, что (3) ~ (2). Пусть
наряду с функцией
на полуоси
определена функция
,
которая, как и функция
, интегрируема по Риману на любом отрезке
,
.
Теорема 2
(признак
сравнения). Пусть
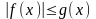 при
при
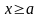 .
Тогда если сходится интеграл
.
Тогда если сходится интеграл
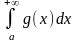 ,
(4) то сходится и интеграл (1). В свою
очередь, если интеграл (1) расходится,
то расходится и интеграл (4). Д о к а з а
т е л ь с т в о. Пусть интеграл (4) сходится.
Тогда по теореме 1 для любого
найдется такое
,
что для любых
выполняется неравенство (2), где вместо
функции
следует
подставить функцию
.
Следовательно, используя неравенство
(
)
получим
,
(4) то сходится и интеграл (1). В свою
очередь, если интеграл (1) расходится,
то расходится и интеграл (4). Д о к а з а
т е л ь с т в о. Пусть интеграл (4) сходится.
Тогда по теореме 1 для любого
найдется такое
,
что для любых
выполняется неравенство (2), где вместо
функции
следует
подставить функцию
.
Следовательно, используя неравенство
(
)
получим
 .
По теореме 1 это означает, что интеграл
(1) сходится. Пусть теперь дано, что
интеграл (1) расходится. Тогда интеграл
(4) также расходится, так как в противном
случае, т.е. в случае его сходимости, по
доказанному выше сходился бы и интеграл
(1), а это противоречит условию. Определение
1. Несобственный
интеграл
называется абсолютно сходящимся, если
сходится интеграл
.
По теореме 1 это означает, что интеграл
(1) сходится. Пусть теперь дано, что
интеграл (1) расходится. Тогда интеграл
(4) также расходится, так как в противном
случае, т.е. в случае его сходимости, по
доказанному выше сходился бы и интеграл
(1), а это противоречит условию. Определение
1. Несобственный
интеграл
называется абсолютно сходящимся, если
сходится интеграл
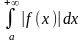 .Определение
2. Если
несобственный интеграл
сходится, но не абсолютно, то говорят,
что он сходится условно.
.Определение
2. Если
несобственный интеграл
сходится, но не абсолютно, то говорят,
что он сходится условно.
