Метод Симпсона

Более высокая точность определения численного значения определенного интеграла получается при аппроксимации функции f(x) квадратичным интерполяционным полиномом, который совпадает с f(x) в крайних точках a и b, а также в средней точке . Интеграл от этого квадратичного полинома выражается формулой:

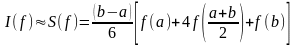, (5)

которая называется формулой Симпсона.

Р ис. 4. Метод Симпсона.

В методе Симпсона площадь криволинейной трапеции рассчитывается как сумма площадей ряда криволинейных трапеций, у которых криволинейная сторона представляет собой участок параболы. Это можно видеть на рис.4.

Каждая парабола может быть проведена только через три граничные точки, принадлежащие двум соседним отрезкам. Поэтому число участков разбиения отрезка [a,b] в отличие от предыдущих методов обязательно должно быть четным. Таким образом, вместо каждых двух элементарных прямолинейных трапеций будем рассматривать одну элементарную трапецию, ограниченную параболической дугой. Исходя из этого, определенный интеграл на случай разбиения интервала на n участков с шагом h. приближенно вычисляется по формуле:

(6)

– полная формула Симпсона.

Таким образом, для реализации метода прямоугольников, трапеции и Симпсона для вычисления определенного интеграла необходимо:

Задать в явном виде определенный интеграл, площадь которого необходимо определить. После этого задаются пределы интегрирования, и шаг интегрирования. Затем проводится расчет по формулам (2), (4) и (6).

Для метода Симпсона число разбиений n должно быть четным, что подлежит проверке при составлении программы.

Метод Гаусса.

Приближение функции одним полиномом на всем отрезке интегрирования, как правило, приводит к большой ошибке в оценке значения интеграла.

Для уменьшения погрешности отрезок интегрирования разбивают на части и применяют численный метод для оценки интеграла на каждой из них.

При стремлении количества разбиений к бесконечности, оценка интеграла стремится к его истинному значению для любого численного метода.

Приведённые выше методы допускают простую процедуру уменьшения шага в два раза, при этом на каждом шаге требуется вычислять значения функции только во вновь добавленных узлах. Для оценки погрешности вычислений используется правило Рунге.

Описанные выше методы используют фиксированные точки отрезка (концы и середину) и имеют низкий порядок точности (0 - методы правых и левых прямоугольников, 1 - методы средних прямоугольников и трапеций, 3 - метод парабол (Симпсона)). Если мы можем выбирать точки, в которых мы вычисляем значения функции , то можно при том же количестве вычислений подынтегральной функции получить методы более высокого порядка точности. Так для двух (как в методе трапеций) вычислений значений подынтегральной функции, можно получить метод уже не 1-го, а 3-го порядка точности:

В общем случае, используя точек, можно получить метод с порядком точности . Значения узлов метода Гаусса по точкам являются корнями полинома Лежандра степени .

Значения узлов метода Гаусса и их весов приводятся в справочниках специальных функций. Наиболее известен метод Гаусса по пяти точкам.

Недостаток метода Гаусса состоит в том, что он не имеет лёгкого (с вычислительной точки зрения) пути оценки погрешности полученного значения интеграла. Использование правила Рунге требует вычисления подынтегральной функции примерно в таком же числе точек, не давая при этом практически никакого выигрыша точности, в отличие от простых методов, где точность увеличивается в разы при каждом новом разбиении. Кронродом был предложен следующий метод оценки значения интеграла

где - узлы метода Гаусса по точкам, а параметров , , подобраны таким образом, чтобы порядок точности метода был равен .

Тогда для оценки погрешности можно использовать эмпирическую формулу:

,

где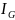 - приближённое значение интеграла, полученное методом Гаусса по точкам.

Сравнение методов по эффективности:

Возьмем пять произвольных промежутков и вычислим погрешность для каждого из методов по формуле:

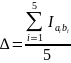
Были выбраны следующие промежутки:

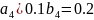
Так как средние значения погрешностей и итераций имеют большой интервал, строить график не имеет смысла, поэтому составим таблицу:

Метод трапеций		Метод Симпсона			Метод Гаусса
Δ	Количество итераций		Δ	Количество итераций		Δ	Количество итераций
4,794001	4,6		4,916453	5,8		0,1203142	61,4
0,216836	63,4		0,000009	46		0,0088742	198,2
0,004717	630,2		0,000004	452,4		0,0056248	637,4
0,003569	6300,8		0,000016	4500,6		0,0000448	1991
						0,0000042	6692,6
						0,0000002	97819,4
						0,0000000	125448,5

Как видно из таблицы, самым лучшим соотношением точность/количество итераций обладает метод Симпсона, но при дальнейшем повышении количества итераций в переменные записываются выходящие за пределы значения, что вносит погрешность в вычисления. Именно поэтому в методе трапеций и Симпсона нижние ячейки оставлены пустыми. Метод Гаусса работает дольше, но при этом может вычислить значение интеграла со сколь угодно большой точностью.

Описание алгоритма решения задачи

Для удобства построения алгоритма была введена функция подсчета значения функции, указанной в задании.

1. Как и в предыдущем задании, был реализован выбор метода решения задачи.

2. До перехода к конкретному методу у пользователя запрашиваются пределы интегрирования. Так как функция определена на промежутке ограничений ввода нет.

3. Метод трапеции начинается с ввода шага с терминала. Далее в результирующую переменную подсчитывается первое слагаемое метода .

4. Стартует цикл, где счетчик выступает в роли аргумента, соответственно он пробегает значения от нижнего предела к верхнему, увеличиваясь каждый раз на шаг. К результирующей переменной каждый раз прибавляется значение .

Примечание: для сокращения кода можно было использовать неупрощенную формулу, тем самым избавиться от строчки, указанной в пункте 3. В самом цикле слагаемое приняло бы вид .

5. Результаты записываются в файл.

6. В методе трапеций запросы вводы и вывод те же самые.

7. Для удобства вычисляется количество разбиений по формуле .

8. По требованию, в методе Симпсона количество разбиений должно быть четным, поэтому в противном случае количество разбиений увеличивается на 1(чтобы не понижать точность) и вычисляется новый шаг.

Примечание: опять же, программу можно упростить, избавившись от этого условия. Для этого достаточно вычислять каждый отрезок не по первой, второй и третьей точке, а по первой третьей и второй, то есть .

9. В цикле выполняются операции, указанные в вышеприведенной формуле для метода Симпсона.

10. Для метода Гаусса введены две функции:

• Первая из них просчитывает значение интеграла на задаваемом в качестве параметра промежутке a, b по формуле

где m= , n= , и 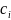- нули полинома Лежандра со степенью 6, значения которых взяты из таблицы:

• Рекурсивная функция, вычисляющая интеграл методом Гаусса с заданной точностью. В качестве параметров используются пределы, ранее вычисленный интеграл и точность. Сначала область интегрирования делится на два, вычисляется по ранее описанной функции, результаты складываются. Если разность суммы и ранее вычисленного интеграла оказывается меньше точности, два раза рекурсивно вызывается функция, первая считает первую половину с точностью, деленной на два и вычисленным интегралом от первой половины, вторая, соответственно от второй. В конце функция возвращает сумму значений вычисленных половинок от интегралов

11. Пользователю предлагается выбрать точность, далее вызывается рекурсивная функция, с параметрами введенных пределов интегрирования, заданной точностью и функцией, вычисляющей значение интеграла на всем заданном промежутке.

12. Результаты записываются в файл

13. С помощью цикла можно еще раз повторить операцию.

Руководство программиста

Программный код приложения разрабатывался на языке СИ.

В программе использованы следующие пользовательские функции:

• float f(float x) вычисляет значение функции от х

• float calcGauss(float a, float b) Вычисляет интеграл методом Гаусса по шести точкам

• float gauss(float a,float b, точность, ранее вычисленный интеграл)

Рекурсивная функция, разбивающая область от a до b на две половинки и считающая интеграл на каждой из них, пока не достигнет нужной точности.

Так же в глобальный массив с двумя строками записаны вышеприведенные точки следующим методом:

double pnt[2][G]={{ , , },

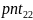{ , , }}; где G – количество точек деленное на два.

То есть внешними скобками объединены строки, а внутренними элементы соответствующей строки. Если потребуется изменить порядок метода Гаусса, нужно во-первых изменить значение константы G и вписать в массив новые значения точек для соответствующего порядка, которые являются табличными значениями.

Блок-схема алгоритма программы приведена в приложении А.

Листинг программы приведен в приложении В.

Пример входного и выходного файла в приложении С.

Руководство пользователя

После запуска программа потребует выбрать метод нахождения интеграла от указанной функции. Далее необходимо задать область интегрирования, после чего для методов Симпсона и трапеции указывается шаг, а для метода Гаусса с шестью узлами - точность. Процедуру можно повторять сколь угодно раз, после чего посмотреть результаты в файле integral.txt

Вывод: В ходе лабораторной работы были изучены некоторые численные методы вычисления определенных интегралов, а так же они были реализованы программно на языке СИ и при помощи специализированных программных пакетов (Matcad).

Приложение В

#include <stdio.h>

#include <stdio.h>

#include <math.h>

#define G 3

double pnt[2][G]={{0.932469514203152/2,0.661209386966265/2,0.238619186083197/2},

{0.171324492379170/2,0.360761573048139/2,0.467913934572691/2}};

float f(float x)

{

float y=(pow(x,2)+sin(2*x))/(cos(x)+3);

return y;

}

float calcGauss(float a,float b)

{

float m,n,sum=0;

m=(b+a)/2;

n=(b-a)/2;

for(int i=0;i<G;i++)

sum+=pnt[1][i]*(f(m+n*pnt[0][i])+f(m-n*pnt[0][i]));

return sum*(b-a);

}

float gauss(float a,float b,float e,float g)

{

float ga,gb,t=(b+a)/2;

ga=calcGauss(a,t);

gb=calcGauss(t,b);

if (fabs(ga+gb-g)>e)

{

ga=gauss(a,t,e/2,ga);

gb=gauss(t,b,e/2,gb);

}

return (ga+gb);

}

void main()

{

float a,b,h,itg;

int N;

char P;

FILE *out;

out=fopen("Integral.txt","w");

printf(" x^2+sin(2*x)\n");

printf("Definite integral of the function Y(x)= ------------\n");

printf(" cos(x)+3\n\n");

printf("can be calculated with ");

do

{

do

{

printf("Simpson method(S), trapetion method(T), Gauss method with 6 nodes(G)\n");

scanf(" %c",&P);

}

while(P!='t' && P!='T' && P!='g' && P!='G' && P!='s' && P!='S');

printf("Input limits(a,b)\n");

scanf("%f %f",&a,&b);

if(P=='t' || P=='T')

{

printf("Input step(h)\n");

scanf("%f",&h);

itg=h*(f(a)+f(b))/2;

for(float i=a+h;i<b;i+=h)

itg+=f(i)*h;

fprintf(out," x^2+sin(2*x)\n");

fprintf(out,"Y(x)= ----------------- = %f\n",itg);

fprintf(out," cos(x)+3\n\n");

fprintf(out,"Integral was calculated from %.3f to %.3f with trapetion method;\nStep was equal %f\n\n",a,b,h);

}

if(P=='S' || P=='s')

{

printf("Input step(h)\n");

scanf("%f",&h);

N=ceil((b-a)/h);

if ((N%2)!=0)

{

N++;

h=(b-a)/N;

}

itg=(f(a)+f(b))*h/3;

for(int i=0;i<=(N/2-1);i++)

{

itg+=f(h*(2*i+1)+a)*4*h/3;

if(i>0)itg+=f(h*2*i+a)*2*h/3;

}

fprintf(out," x^2+sin(2*x)\n");

fprintf(out,"Y(x)= ----------------- = %f\n",itg);

fprintf(out," cos(x)+3\n\n");

fprintf(out,"Integral was calculated from %.3f to %.3f with Simpson's method;\nStep was equal %f\n\n",a,b,h);

}

if(P=='G' || P=='g')

{

printf("Input accuracy(h)\n");

scanf("%f",&h);

itg=gauss(a,b,h,calcGauss(a,b));

fprintf(out," x^2+sin(2*x)\n");

fprintf(out,"Y(x)= ----------------- = %f\n",itg);

fprintf(out," cos(x)+3\n\n");

fprintf(out,"Integral was calculated from %.3f to %.3f with Gauss method;\nAccuracy was equal %f\n\n",a,b,h);

}

printf("You may check results in 'Integral.txt file'\nDo you want to try again?(Y/N)\n");

scanf(" %c",&P);

}

while(P=='Y' || P=='y');

fclose(out);

}

Приложение C

Выходной файл Integral.txt:

x^2+sin(2*x)

Y(x)= ----------------- = 17.123938

cos(x)+3

Integral was calculated from 0.000 to 5.000 with trapetion method;

Step was equal 0.001000

x^2+sin(2*x)

Y(x)= ----------------- = 17.116716

cos(x)+3

Integral was calculated from 0.000 to 5.000 with Simpson's method;

Step was equal 0.001000

x^2+sin(2*x)

Y(x)= ----------------- = 17.116722

cos(x)+3

Integral was calculated from 0.000 to 5.000 with Gauss method;

Accuracy was equal 0.001000

x^2+sin(2*x)

Y(x)= ----------------- = 0.276663

cos(x)+3

Integral was calculated from 0.000 to 1.000 with trapetion method;

Step was equal 0.000100

15