3.1.2. Таблицы истинности

3.8. Установить равносильность формул

(Х  Y) и

Решение

Х	Y			Х  Y
0	0	1	1	1	1	1	1
0	1	1	0	0	1	0	0
1	0	0	1	0	0	1	0
1	1	0	0	1	1	1	1

3.9. Составить таблицу истинности для формулы

(Х  Y)   Y.

3.10. Составить таблицу истинности для формулы

Х₁  Х₂  Х₃.

3.11. Составить таблицу истинности для формулы:

(Х  (Х  Е))  Y.

3.2. Булевы функции

Числа в цифровых устройствах представляются в различных системах счислениях (позиционных и непозиционных).

В цифровой технике применяются десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. В двоичной системе счисления алфавит содержит два символа {0,1}. С их помощью записываются все слова (числа). При использовании n разрядов можно записать 2ⁿ различных наборов двоичных комбинаций чисел (слов).

Переход из одной системы счисления в другую осуществляется в соответствии с приведенной выше формулой записи полинома А. Например,

.

Математической основой работы цифровых устройств в двоичной системе счисления является алгебра логики или булева алгебра.

Функция f(x₀, x₁, …, x_n) называется логической (булевой), если ее аргументы x₀, x₁, …, x_n и значения функции могут принимать только два значения: логического 0 и логической 1.

Для задания функции алгебры логики, как и любой другой функции необходимо поставить в соответствие значения функции для всех возможных комбинаций входных аргументов. Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n.

Способы задания логических функций: словесный (взаимосвязь функции и ее аргументов описывается словесной формулировкой); табличный (строится таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие значения логической функции); цифровой (функцию алгебры логики определяют в виде последовательности десятичных чисел, при этом последовательно расписывают эквиваленты двоичных кодов, которые соответствуют единичным либо нулевым значениям функции); аналитический (функция алгебры логики записывается в виде аналитического выражения, где показаны логические операции, выполняемые над аргументами функции).

Логические функции одной или двух переменных называются элементарными. Они предполагают проведение только одной логической операции.

Существует 4 функции одной переменной (табл. 3.2).

Таблица 3.2

Таблица истинности для функций одной переменной

Аргумент х	Функции
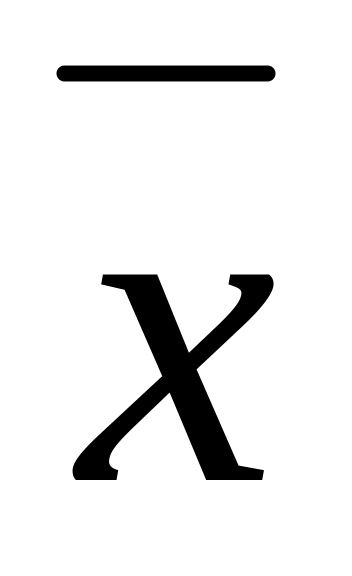
	f0(х) = 0	f1(х) = х	f2(х) =	f3(х) = 1
0 1	0 0	0 1	1 0	1 1

Существует 16 функций двух переменных (табл. 3.3).

Таблица 3.3

Таблица истинности для функций двух переменных

Аргу- менты		Функции
х1	х2	f0=0	f1= x1x2	f2= х1х2	f3= х1	f4= х2х1	f5= х2	f6 х1х2	f7== х1+х2	f8=х1х2	f9=х1х2	f10= х2	f11=х1х2	f12=  х1	f13=х1х2	f14= х1х2	f15=1
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Цифровую форму представления логической функции рассмотрим на примере функции f₆, которая принимает единичные значения на наборах входных переменных (х₁х₂) в двоичном коде 01, 10, что соответствует десятичному эквиваленту 1; 2: f₆(х₁, x₂)=(1,2)=(1,2). Функция f₆ принимает нулевые значения на наборах входных переменных (х₁х₂) в двоичном коде 00,11. Это соответствует в десятичном коде 0; 3: f₆(х₁, x₂)=П(0,3)=(0,3).

Таблицы истинности могут быть записаны в других формах, которые могут оказаться более удобными в различных случаях. Например, при записи таблицы истинности в виде карты Карно аргументы функции (входные переменные) делятся на две группы. Комбинации значений аргументов одной группы приписываются столбцам таблицы, комбинации значений аргументов другой группы — строкам таблицы. Столбцы и строки обозначаются комбинациями, соответствующими последовательности чисел в коде Грея.

Минимизация логических функций — это упрощение логического выражения с целью уменьшения аппаратур­ных затрат при технической реализации цифрового уст­ройства. С целью про­ведения расчетов и проектирования целесообразно зако­ны функционирования представлять в стандартных кано­нических формах. Для проведения последующих преобразований логи­ческие функции представляют в исходных стандартных канонических формах: совер­шенной дизъюнктивной нормальной форме (СДНФ) и со­вершенная конъюнктивной нормальной форме (СКНФ).

Записывают СДНФ и СКНФ по таблице истинности: СДНФ имеет столько конъюн­кций, сколько единичных значений принимает функция. Для каждого набора переменных, для которых логичес­кая функция равна логической 1, составляются элементар­ные конъюнкции. Если в данном наборе входная переменная имеет нулевое значение, то ее записывают с инверсией. Затем логически суммируют все конъюнкции.

Если любая из конъюнкций равна логической 1, то фун­кция принимает единичное значение. Ранг конъюнкции n определяется числом входящих в нее переменных. Каждая конъюнкция в СДНФ имеет ранг n, равный числу переменных логической функции. В состав ДНФ входят конъюнкции с рангом меньше n.

СКНФ также может быть записана непосредственно по таблице истинности.

В цифровых устройствах техническую реализацию логических функций осуществляют логические элемен­ты. Условные графические обозначения (УГО) наиболее распространенных элементов НЕ, И, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ, исключающее ИЛИ-НЕ, показаны на рис. 3.1.

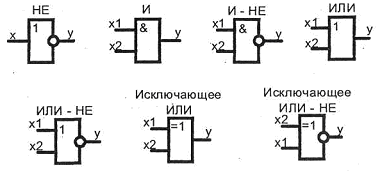
Рис. 3.1. Условные графические обозначения наиболее распространенных элементов