Дифференциальные уравнения второго порядка

Пусть дано дифференциальное уравнение второго порядка F(x,y,y^',y^'') = 0 . Двухточечная краевая задача для уравнения ставится следующим образом: найти функцию y = y(x), которая внутри отрезка [a,b] удовлетворяет уравнению, а на концах отрезка - краевым условиям

.

Рассмотрим случай, когда уравнение и граничные условия линейны.Такая краевая задача называется линейной краевой задачей. В этом случае дифференциальное уравнение и краевые условия записываются так: y^'' + p(x)y^' + q(x)y = f(x),

,

где p(x),q(x),f(x)- известные непрерывные на отрезке [a,b] функции, α₀,α₁,β₀,β₁,A,B -заданные постоянные, причем .

Если А=В=0, то краевые условия называются однородными. Методы приближенного решения поставленных краевых задач можно разбить на две группы: разностные методы и аналитические методы.

Метод конечных разностей для линейных дифференциальных уравнений второго порядка

Пусть x₀ = a,x_n = b,x_i = x₀ + ih(i = 1,2,...,n − 1) - система равноотстоящих узлов с некоторым шагом и p_i = p(x_i),q_i = q(x_i),f_i = f(x_i) . Обозначим получаемые в результате расчета приближенные значения искомой функции y(x) и ее производных y^'(x),y^''(x) в узлах x_i через соответственно. Заменим приближенно в каждом внутреннем узле производные y^'(x_i),y^''(x_i) конечно-разностными отношениями , а на концах положим . Используя эти формулы , приближенно заменим уравнение y^'' + p(x)y^' + q(x)y = f(x) и краевые условия системой уравнений

.

Получим линейную алгебраическую систему n+1 уравнений с n+1 неизвестными. Решив ее, если это возможно, получим таблицу приближенных значений искомой функции.

Более точные формулы получаются, если заменить y^'(x_i),y^''(x_i) центрально-разностными отношениями . Тогда получим систему

.

Оценка погрешности метода конечных разностей имеет вид ,где y(x_i)-значение точного решения при x = x_i,M₄ = max_[a,b] | y⁽⁴⁾(x) | .

В практических задачах часто встречаются уравнения, в которых функции p(x),q(x),f(x) заданы таблично с некоторым шагом h. Совершенно естественно такие уравнения решать разностным методом с данным шагом h.

Метод прогонки

1. Рассмотрим систему, полученную при замене уравнения и краевых условий конечно-разностными отношениями:

.

Метод прогонки решения таких систем заключается в следующем. Запишем сначала первые n-1 уравнений системы в виде

y_{i + 2} + m_iy_{i + 1} + k_iy_i = h²f_i, где m_i = − 2 + hp_i,k_i = 1 − hp_i + h²q_i,(i = 0,1,2,...,n − 2).

Затем написанная выше система приводится к виду y_{i + 1} = c_i(d_i − y_{i + 2}),(i = 0,1,2,...,n − 2). Числа c_i,d_i последовательно вычисляются по формулам:

при i=0 ;

при i=1,2,...,n-2 .

Вычисления производятся в следующем порядке.

ПРЯМОЙ ХОД. По формулам вычисляем значения m_i,k_i.Находим c₀d₀ и затем, применяя последовательно рекуррентные формулы, получаем значения c_id_i при i = 1,2,...,n − 2 .

ОБРАТНЫЙ ХОД.Из уравнения при i=n-2 и последнего уравнения системы получаем .

Решив эту систему относительно y_n, будем иметь Используя уже известные числа c_{n − 2}d_{n − 2}, находим y_n. Затем вычисляем значения y_i(i = n − 1,...,1),последовательно применяя рекуррентные формулы:

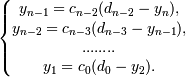
Значение y₀ находим из предпоследнего уравнения системы: .

2. Рассмотрим метод прогонки для решения системы, которая получается при замене уравнения и второго краевого условия центральными конечно-разностными отношениями:

.

Запишем сначала первые n-1 уравнений системы в виде , где . Затем приводим эти уравнения к виду y_i = c_i(d_i − y_{i + 1}),(i = 1,2,...,n − 1), где коэффициенты c_i,d_i вычисляются по формулам: при i=1 ; при i=2,...,n-2 .

Вычисления производятся в следующем порядке.

ПРЯМОЙ ХОД. По формулам вычисляем значения m_i,k_i.Находим c₁d₁ и затем, применяя последовательно рекуррентные формулы, получаем значения c_id_i при i = 2,...,n − 2 .

ОБРАТНЫЙ ХОД.Запишем уравнение при i = n,i = n − 1 и последнее уравнение системы: .

Решая эту систему относительно y_n, будем иметь Используя уже известные числа c_n,d_n,c_{n − 1}d_{n − 1}, находим y_n. Значения y_i(i = n − 1,...,1)получаем из рекуррентных формул.

Значение y₀ находим из предпоследнего уравнения системы: .