
- •Содержание
- •4. Численные квадратуры 4
- •4. Численные квадратуры
- •4.1. Введение
- •4.2. Одномерные квадратурные правила и формулы
- •4.3. Формулы прямоугольников
- •4.4. Формула трапеций
- •4.5. Метод Ньютона-Котесса
- •4.6. Формула Симпсона (метод парабол)
- •If Odd(k) then {Проверка k на нечетность}
- •4.8. Формула Уэддля (Веддля)
- •4.10. Метод Чебышева
- •4.11. Метод Гаусса
- •4.12. Переход от одного отрезка к другому
- •4.13. Квадратурные правила Гаусса-Кронрода
- •4.14. Интегрирование таблично заданных функций
- •4.15. Эрмитова кубическая квадратура
- •4.16. Двойные и тройные интегралы
- •Литература
4.12. Переход от одного отрезка к другому
Программы, в которых
реализованы квадратурные правила,
обычно позволяют задавать концы отрезка
интегрирования произвольно
.
Однако в таблицах, правила приведены
для какого-либо определенного отрезка,
чаще всего
![]() или
или
![]() .
Приближенное значение интеграла
.
Приближенное значение интеграла
![]() для какого-либо другого отрезка
для какого-либо другого отрезка
![]() будет иметь вид
будет иметь вид
![]() .
.
В этом случае нужно
с помощью замены переменной осуществить
переход от переменной
![]() ,
принадлежащей отрезку
( где возможно
,
принадлежащей отрезку
( где возможно
![]() )
к переменной
)
к переменной
![]() ,
принадлежащей отрезку
,
принадлежащей отрезку
![]() .
Тогда формула примет вид
.
Тогда формула примет вид
![]()
Для отрезка она упростится
![]() .
.
Существует много преобразований при переходе от переменной к переменной и преобразовании отрезка к отрезку , но приведенное выше – самое простое в силу своей линейности.
4.13. Квадратурные правила Гаусса-Кронрода
Вычисление определённых интегралов находит широкое применение как в математических, так и в прикладных задачах. На практике, как правило, используют приближённые квадратурные формулы. Одной из наиболее известных и востребованных при разработке пакетов компьютерной математики (MATLAB, Mathematica) является квадратурная формула Гаусса-Кронрода [1-6].
При построении
квадратурных формул типа Гаусса-Кронрода
используются различные системы
ортогональных многочленов [1-4, 6].
Рассмотрим систему ортогональных
многочленов Якоби
![]() .
Нетрудно доказать следующее свойство
симметрии этих многочленов.
.
Нетрудно доказать следующее свойство
симметрии этих многочленов.
ТЕОРЕМА. Для
многочленов Якоби
,
ортогональных на
![]() с весовой функцией
с весовой функцией
![]() (
(![]() ,
,
![]() ),
выполняется
),
выполняется
![]() .
.
Для весовой функции
вида
при
![]() эта теорема обобщает доказанное в [7]
утверждение (Теорема 1.3).
эта теорема обобщает доказанное в [7]
утверждение (Теорема 1.3).
В настоящей работе показано, что для базовой формулы типа Гаусса (построенной с помощью многочленов Якоби), используя указанное свойство симметрии, можно построить две парные симметричные квадратурные формулы типа Гаусса-Кронрода.
Не теряя общности,
будем рассматривать промежуток
интегрирования
![]() .
Пусть построена базовая квадратурная
формула типа Гаусса
.
Пусть построена базовая квадратурная
формула типа Гаусса
![]() , (1)
, (1)
где весовые
коэффициенты
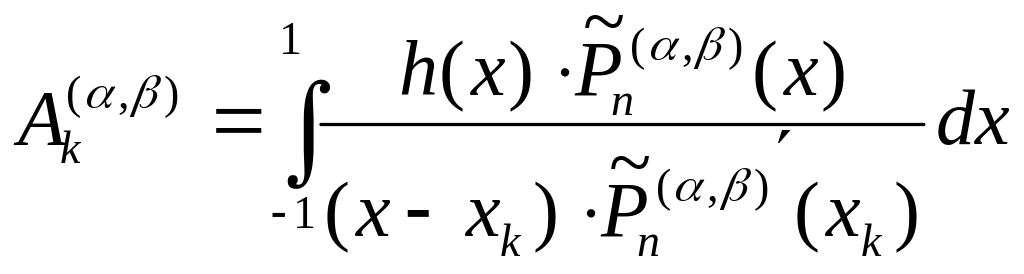 ,
,
![]() – нули многочлена Якоби с единичным
старшим коэффициентом
– нули многочлена Якоби с единичным
старшим коэффициентом
![]() .
Тогда по найденным значениям весовых
коэффициентов
.
Тогда по найденным значениям весовых
коэффициентов
![]() и узлам
и узлам
![]()
![]() можно построить две парные симметричные
формулы типа Гаусса-Кронрода (равного
алгебраического порядка точности):
можно построить две парные симметричные
формулы типа Гаусса-Кронрода (равного
алгебраического порядка точности):
![]() , (2)
, (2)
![]() , (3)
, (3)
где
– нули полинома Кронрода
![]() ,
который строится по аналогии с методом,
изложенным в [4]. Коэффициенты многочлена
,
который строится по аналогии с методом,
изложенным в [4]. Коэффициенты многочлена
![]() определяются с помощью взвешенных
степенных моментов
определяются с помощью взвешенных
степенных моментов
![]() по формулам
по формулам
![]()
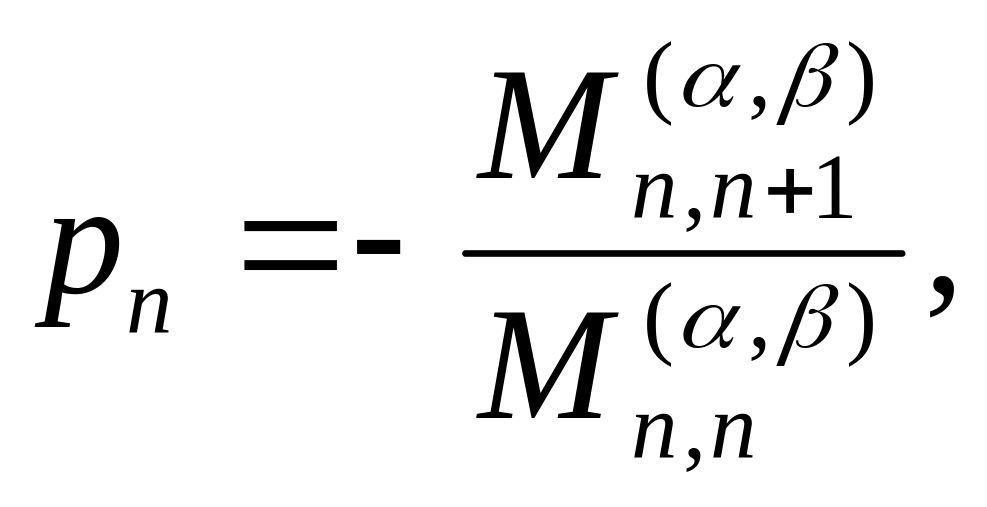
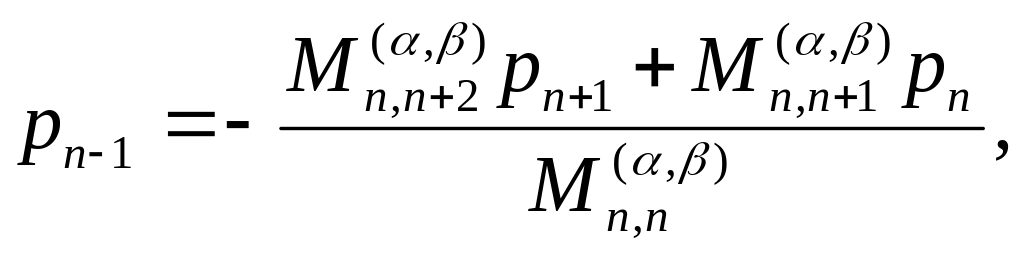 …
…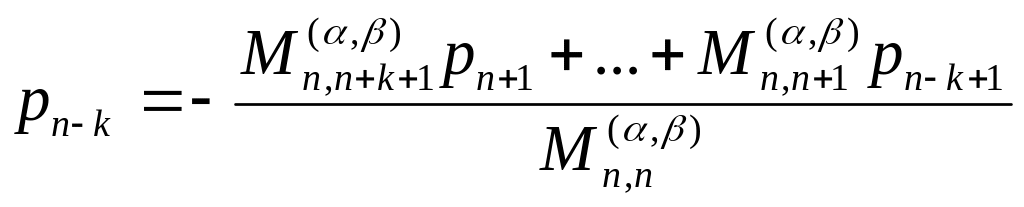 ,
а весовые коэффициенты вычисляются по
формуле
,
а весовые коэффициенты вычисляются по
формуле
 .
.
Заметим, что правые
части в формулах (2) и (3) в общем случае
при
дают различные приближенные значения
интеграла, а при
![]() – равные. Получение двух приближенных
значений интеграла с помощью одного
набора весовых коэффициентов
и узлов
дает определенные вычислительные и
алгоритмические преимущества при
использовании формул (2) и (3).
– равные. Получение двух приближенных
значений интеграла с помощью одного
набора весовых коэффициентов
и узлов
дает определенные вычислительные и
алгоритмические преимущества при
использовании формул (2) и (3).
В [4] указано, что
формулы (1) и (2)–(3) при некоторых
ограничениях на весовую функцию можно
применять при вычислении интегралов
вида
![]() ,
предварительно выделив весовую функцию
и положив
,
предварительно выделив весовую функцию
и положив
![]() .
.
В 1965 году задачу
получения оценок погрешности квадратурных
правил Гаусса исследовал советский
специалист в области вычислительной
математики А. С. Кронрод. Идея Кронрода
состояла в построении, наряду с правилами
Гаусса, нового правила, узлами которого
были бы как все узлы правила Гаусса (![]() ),
так и некоторые другие точки. Кронрод
предложил строить правила вида
),
так и некоторые другие точки. Кронрод
предложил строить правила вида
![]() .
.
Отметим, что
и
![]() имеют
общих узлов. Кроме того,
имеет
дополнительных узлов и новые веса
имеют
общих узлов. Кроме того,
имеет
дополнительных узлов и новые веса
![]() .
Два правила (
,
)
называют парой
Гаусса-Кронрода.
.
Два правила (
,
)
называют парой
Гаусса-Кронрода.
Таблица весов для пары Гаусса-Кронрода (7,15) для отрезка .
-
Узлы
7-точечтого правила Гаусса
Веса


-
Узлы
15-точечтого правила Крондора
Веса

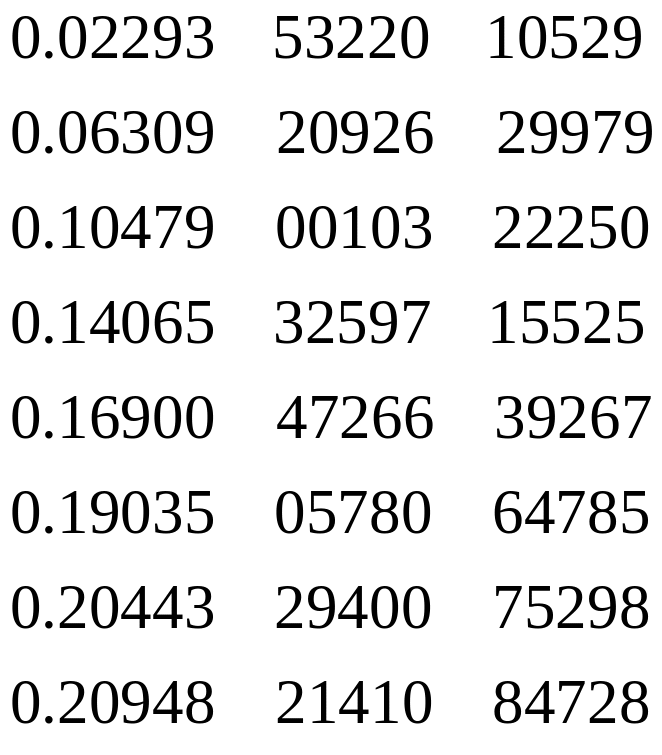
Оценка погрешности правила Гаусса-Кронрода
![]() .
.
Пара Гаусса-Кронрода
вместе с приведенной оценкой погрешности
сейчас представляет собой один из самых
эффективных методов вычисления интегралов
общего вида. Пара (![]() ,
,![]() )
является стандартной.
)
является стандартной.
