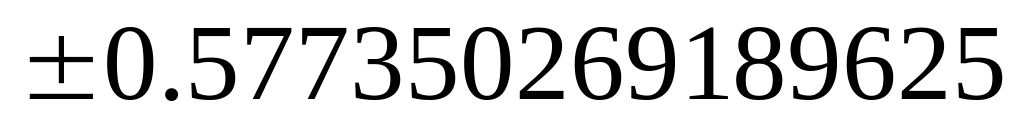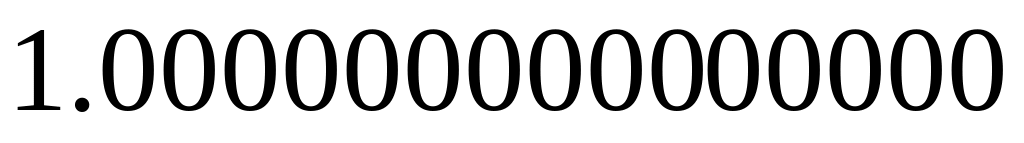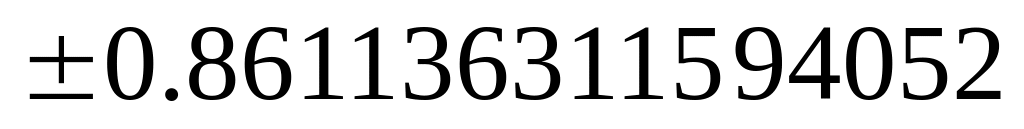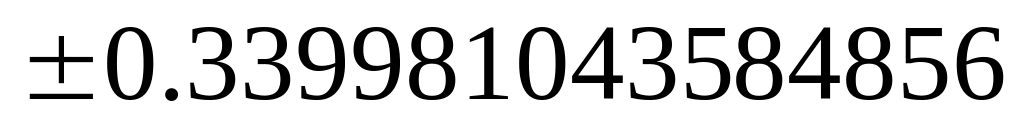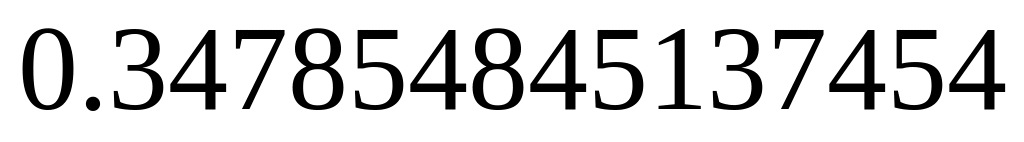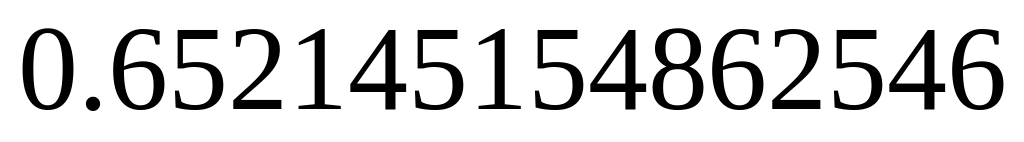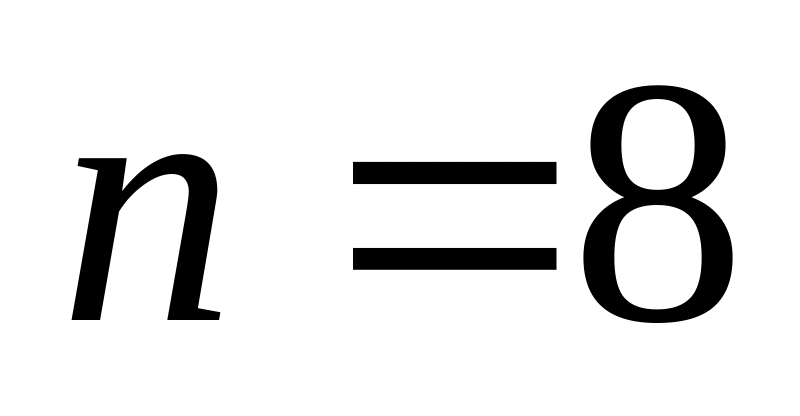If Odd(k) then {Проверка k на нечетность}

I:= I + 4.0 * Fun(A+k*h)

else

I:= I + 2.0 * Fun(A+k*h);

Simpson:= (I + Fun(B)) * h / 3.0

End; {Simpson}

{Головная программа}

BEGIN

ClrScr;{Очищает экран, модуль Crt}

WriteLn (' ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА МЕТОДОМ СИМПСОНА');

WriteLn;

WriteLn (' ИСХОДНОЕ УРАВНЕНИЕ: y = Cos(x*x)');

WriteLn('Введите исходные данные:');

Write('Начало интервала интегрирования A= '); ReadLn(A);

Write('Конец интервала интегрирования B= '); ReadLn(B);

Write('Количество интервалов разбиения N= '); ReadLn(N);

WriteLn;

Int:= Simpson(Fun, A, B, N);

WriteLn (' **************** РЕЗУЛЬТАТ ****************');

WriteLn(' Значение интеграла: ',Int:12:10);

WriteLn;

WriteLn(' ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ ЛЮБУЮ КЛАВИШУ!!!');

Repeat Until KeyPressed; {Ожидает нажатия любой клавиши, модуль Crt}

ClrScr;{Очищает экран, модуль Crt}

END.

4.7. Формула Ньютона-Котесса при n=4 (формула Бодэ)

Численное интегрирование методом Ньютона-Котеса при (формула Боде):

4.8. Формула Уэддля (Веддля)

Метод Уэддля (Веддля) базируется на применении к каждому из отрезков разбиения формулы

Метод применяют в частном случае, когда . Это метод пятого порядка для шести точек.

4.9. Формула Ньютона-Котесса (n=6)

Формула с повышенной точностью (в сравнении с формулой Уэддля) для

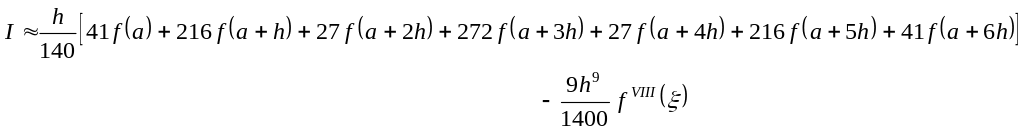
метод седьмого порядка для шести точек.

4.10. Метод Чебышева

Метод основан на вычислении определенного интеграла по формуле

Этот интеграл приводится к виду

подстановкой

.

Выбор значений производится из условия, что формула интегрирования будет точной для вида, , т. е. для полиномом вплоть до -й степени.

Для ,

для

Формула точна для полинома степени .

4.11. Метод Гаусса

Говорят, что -точечное квадратурное правило имеет алгебраическую степень точности , если его остаток равен нулю для любого полинома степени , но не равен нулю для некоторого полинома степени .

Алгебраическая степень точности правил трапеций и прямоугольников равна 1 . Алгебраическая степень точности правила Симпсона равна 3.

Квадратурные правила редко используются для интегрирования полиномов, но разумно предположить, что чем больше алгебраическая степень точности квадратурного правила, тем оно лучше. Поэтому правилам высокой алгебраической степени точности отдается предпочтение, хотя на практике часто более важным являются особенности стратегии применения правила, а не оно само.

Если проинтегрировать лагранжев интерполяционный полином , проходящий через точки , то придём к правилу

, где .

Правила такого типа называются интерполяционными. Наиболее известные квадратурные правила получаются, если выбрать точки равноотстоящими на отрезке интегрирования; такие правила называются правилами Ньютона-Котеса. Правила трапеций и Симпсона представляют собой правила Ньютона-Котеса невысоких алгебраических степеней точности. Правила же Ньютона-Котеса, алгебраическая степень точности которых высока, обладают, к сожалению, тем свойством, что среди их весов имеются отрицательные. Обычно это не желательный эффект, поскольку интегрирование положительной функции может привести к искажению результата из-за катастрофической потери значащих разрядов.

Получим квадратурную формулу Гаусса на произвольное число узлов

,

в которой ни ни заранее не предписаны, а выбираются таким образом, чтобы правило было точным для полиномов наиболее высокой степени. Для любого существует единственная квадратурная формула Гаусса. Её алгебраическая степень точности равна , причём -точечной формулы большей алгебраической степени точности не существует. В этом смысле формула Гаусса является наилучшей.

Если имеет непрерывных производных на , то

.

Относительно известно лишь, что .

Правила Гаусса принадлежат к наиболее часто применяемым правилам на практике.

Перечислим их свойства.

1. За небольшим исключением, веса и узлы правил Гаусса иррациональны. При , веса 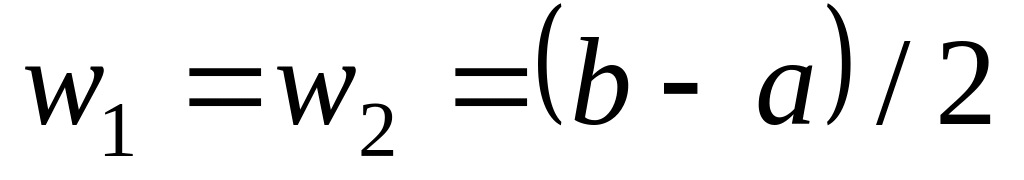. Кроме того, если нечётно, то один из узлов совпадает с серединой отрезка интегрирования .

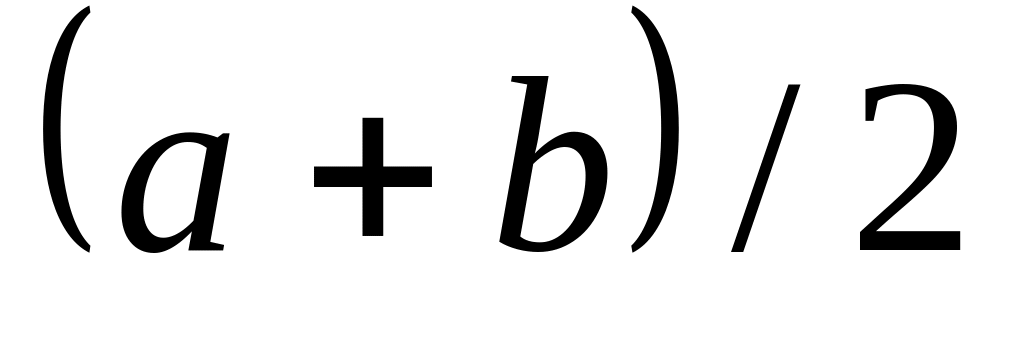2. Правила Гаусса относятся к правилам открытого типа. Это означает, что ни один из узлов не совпадает ни с одним из концов отрезка интегрирования 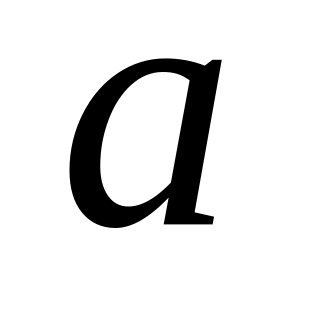или .

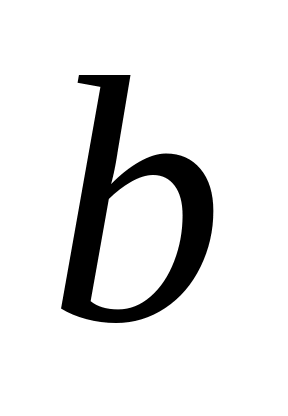3. Множества узлов двух правил Гаусса почти не пересекаются. Иными словами, узлы -точечного правила отличается от узлов 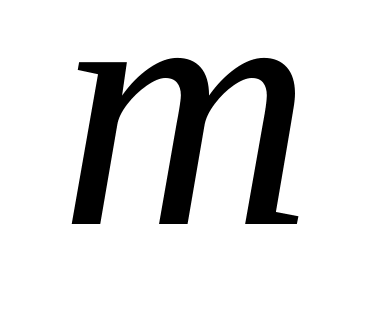-точечного правила. Исключение состоит в том, что если нечётно, то один из узлов совпадает с серединой отрезка интегрирования.

4. Вывод правил Гаусса позволяет предположить, что если подынтегральная функция близка к полиному, то правило Гаусса наиболее пригодно для вычисления интеграла от такой функции.

5. Правила Гаусса являются интерполяционными. Это означает, что если мы возьмём узлов -точечной формулы Гаусса и соответствующих значений 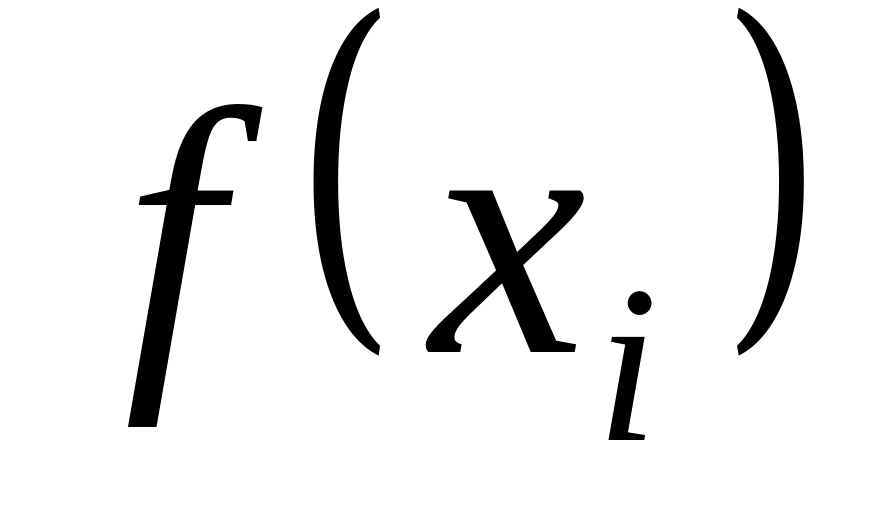и построим тот единственный полином степени 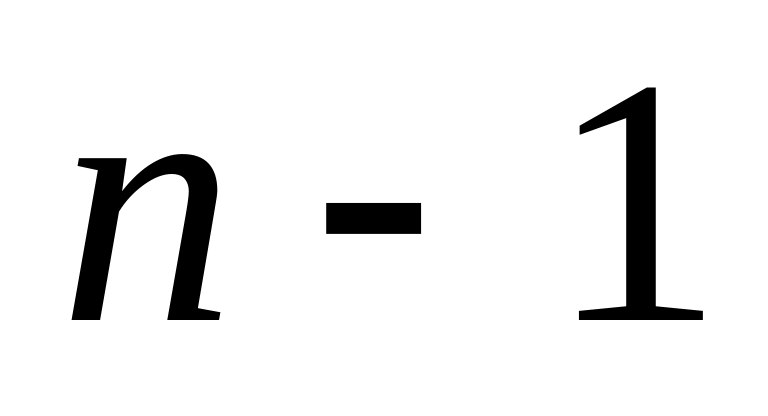, который интерполирует эти данные, то интегрирование по отрезку построенного полинома даст нам тот же результат, что и применение к формулы Гаусса.

6. Существует тесная связь между квадратурами Гаусса и ортогональными полиномами. Узлы -точечного правила Гаусса являются нулями полинома Лежандра степени . Из-за этого эти квадратуры часто называют также квадратурами Гаусса-Лежандра.

Некоторые квадратуры Гаусса для интеграла

Узлы	Веса