- •Содержание
- •3. Интерполялия, экстрополяция, аппроксимация, сглаживание 5
- •3. Интерполялия, экстрополяция, аппроксимация, сглаживание
- •3.1. Введение
- •3.2. Интерполяция
- •3.2.1. Полиномиальная интерполяция
- •Аппроксимационная теорема Вейерштрасса.
- •3.2.2. Вычисление значений многочлена. Схема Горнера
- •3.2.3. Линейная интерполяция
- •3.2.4. Квадратичная интерполяция
- •3.2.5. Построение других базисных функций
- •3.2.6. Многочлены Тейлора
- •3.2.7. Лагранжева интерполяция
- •I, j, n : Integer;
- •3.2.8. Ошибки полиномиальной интерполяции
- •3.2.9. Кусочно-линейная интерполяция
- •Var X,y : Array[0..N] of Real;
- •I,j : Integer;
- •Var f:Real;
- •3.2.10. Кусочно-кубическая интерполяция
- •3.2.11. Эрмитов кубический интерполянт
- •3.2.12. Кубические сплайны
- •Var r, s, l : Vect;
- •Var l, I, j : Integer;
- •1 : Begin
- •0 : Begin
- •Var XX:RealType;
- •3.2.13. Кривые Безье. Сплайны
- •3.2.14. Итерационный способ вычисления интерполяционного полинома (способ Эйткена)
- •3.2.15. Интерполяционный многочлен Ньютона
- •3.2.16. Интерполяционный многочлен Гаусса
- •3.2.17. Интерполяционный многочлен Стирлинга
- •3.2.18. Интерполяционный многочлен Эверетта
- •3.3. Аппроксимация данных методом наименьших квадратов
- •3.3.1. Аппроксимация данных методом наименьших квадратов
- •3.3.2. Аппроксимация данных с другими нормами
- •3.3.3. Аппроксимация данных многочленом заданной степени
- •Var X,y:array[1..Nmax] of real;
- •I,n:integer;
- •Литература
- •Простейшие способы интерполяции
- •Интерполяционные полиномы
- •Сплайн-интерполяция
- •Тригонометрическая интерполяция
- •Неклассические методы интерполяции
- •Реконструкция функций
- •Всюду гладкая интерполяция
3.2.14. Итерационный способ вычисления интерполяционного полинома (способ Эйткена)
Для линейного интерполирования имеем
![]() (*)
(*)
В случае, когда точность линейной интерполяции недостаточна, необходимо повышать степень интерполяционного многочлена, привлекая большее число значений .
В частности, интерполяционный многочлен
второй степени, проходящий через точки
![]() ,
может быть вычислен по формуле
,
может быть вычислен по формуле
![]() ,
(**)
,
(**)
где
![]() и
и
![]() определены по (*).
определены по (*).
Многочлен третьей степени, проходящий
через точки
![]() ,
определяется аналогичной формулой
,
определяется аналогичной формулой
![]() .
(***)
.
(***)
Интерполяционный многочлен
й
степени, принимающий в точках
![]() соответственно табличные значения
соответственно табличные значения
![]() ,
определяется формулой
,
определяется формулой
![]() .
(****)
.
(****)
Это и есть итерационный способ Эйткена.
3.2.15. Интерполяционный многочлен Ньютона
Интерполяционный многочлен Ньютона для неравномерных промежутков может быть представлен в виде
![]() ,
(*)
,
(*)
где
![]() .
.
Величина
![]() носит название разделённой разности
носит название разделённой разности
![]() го
порядка.
го
порядка.
В случае равных промежутков формула
(*) упрощается, сделаем замену переменной
![]() ,
получим
,
получим
![]() ,
(**)
,
(**)
где
![]() ,
,
![]() - конечные разности первого порядка,
- конечные разности первого порядка,
![]() - конечные разности второго порядка
и т. д.
- конечные разности второго порядка
и т. д.
Формула (**) носит название интерполирования вперёд.
Сделаем замену
![]() ,
получим формулу для интерполирования
назад
,
получим формулу для интерполирования
назад
![]() .
(***)
.
(***)
Здесь
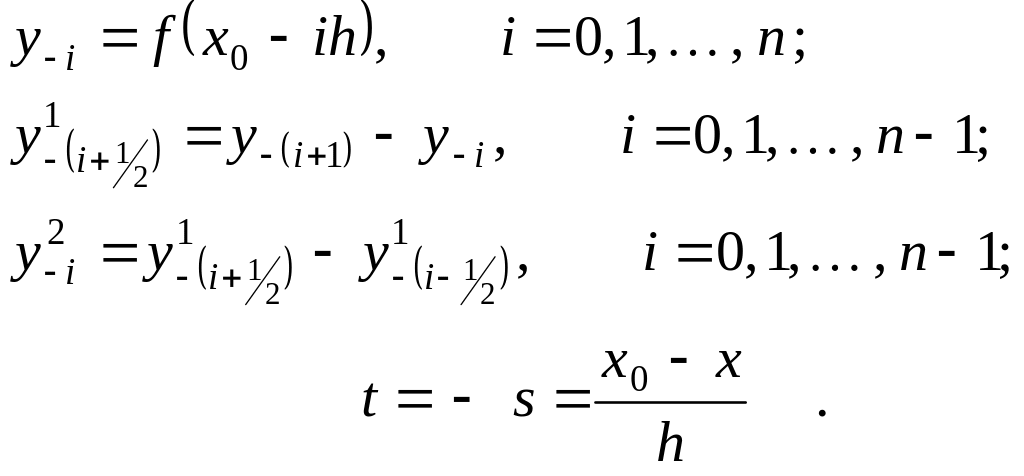
Остаточные члены для (**) и (***) выражаются соответственно
![]() и
и
![]() .
.
3.2.16. Интерполяционный многочлен Гаусса
Интерполяционные формулы с центральными
разностями. Рассмотрим в качестве узлов
![]() точки
точки
![]() ,
получим интерполяционную формулу
Гаусса для интерполяции вперёд
,
получим интерполяционную формулу
Гаусса для интерполяции вперёд
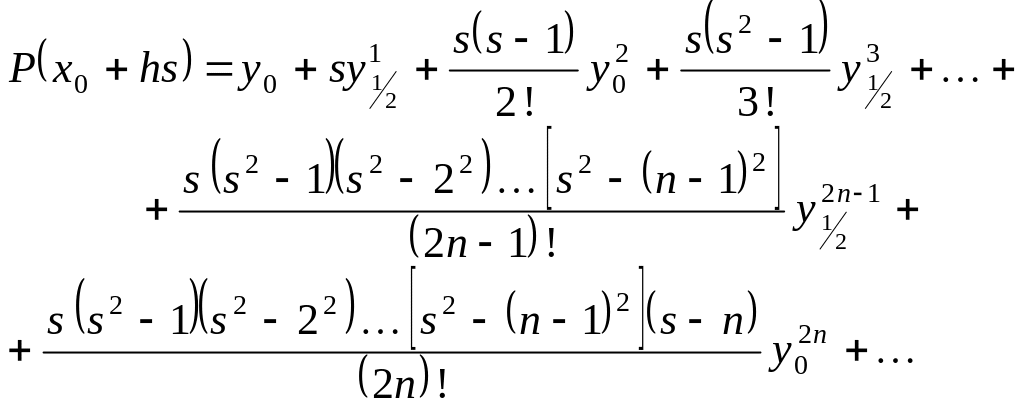 (G*)
(G*)
Если взять в качестве узлов
![]() ,
то получим интерполяционную формулу
Гаусса для интерполяции назад
,
то получим интерполяционную формулу
Гаусса для интерполяции назад
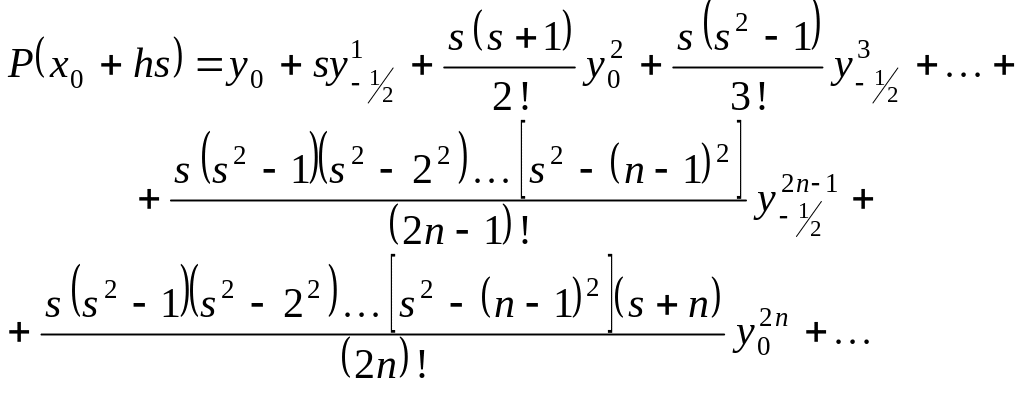 (G**)
(G**)
3.2.17. Интерполяционный многочлен Стирлинга
Полусумма (G*) и (G**) даёт формулу Стирлинга
 (S)
(S)
Здесь используются разности чётного
порядка с индексом
![]() и полусуммы разностей нечётного порядка
с индексами
и полусуммы разностей нечётного порядка
с индексами
![]() и
и
![]() :
:
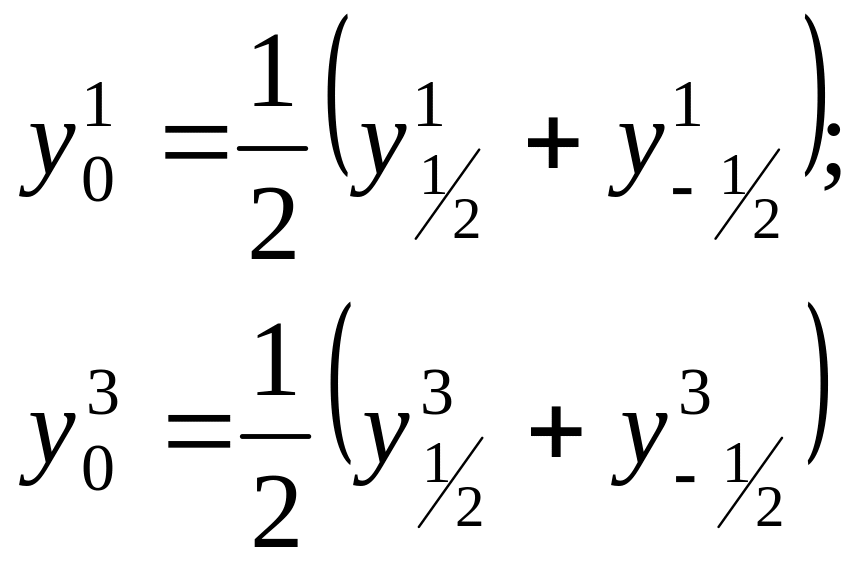 .
.
3.2.18. Интерполяционный многочлен Эверетта
Исключив из интерполяционной формулы (G*) разности нечётного порядка, получим важную формулу Эверетта:
![]() ,
(E)
,
(E)
где
![]() ,
а разности, используемые в формуле,
подчёркнуты в таблице
,
а разности, используемые в формуле,
подчёркнуты в таблице
3.2.19. Интерполяционный многочлен Бесселя
Приведём формулу Бесселя
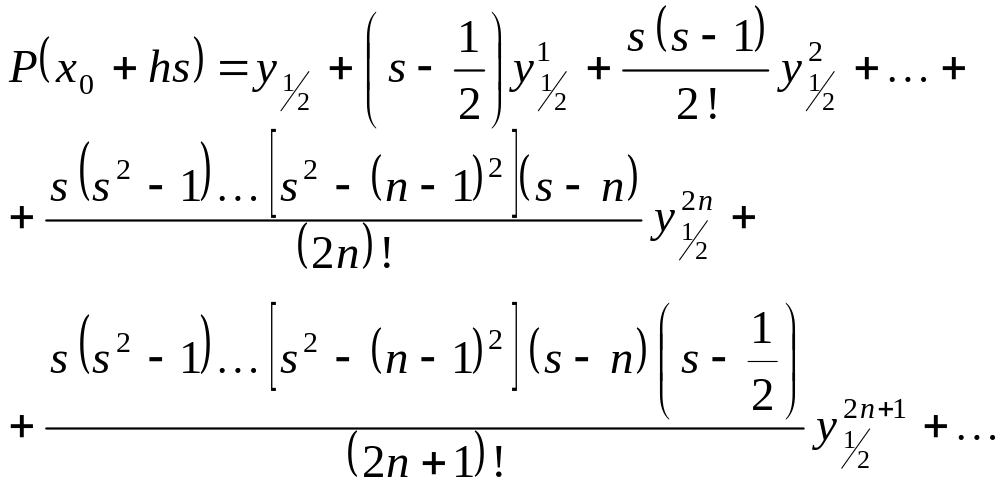
Здесь
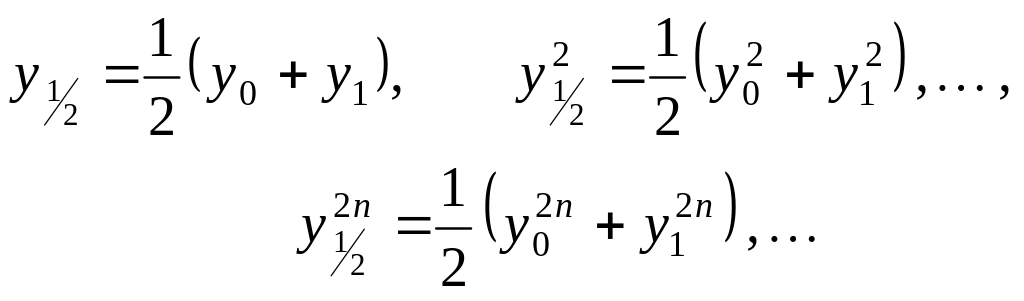
3.2.20. Тригонометрическое интерполирование
Периодические функции интерполируют тригонометрическими многочленами вида:
![]()
Общее решение интерполяционной задачи даёт многочлен
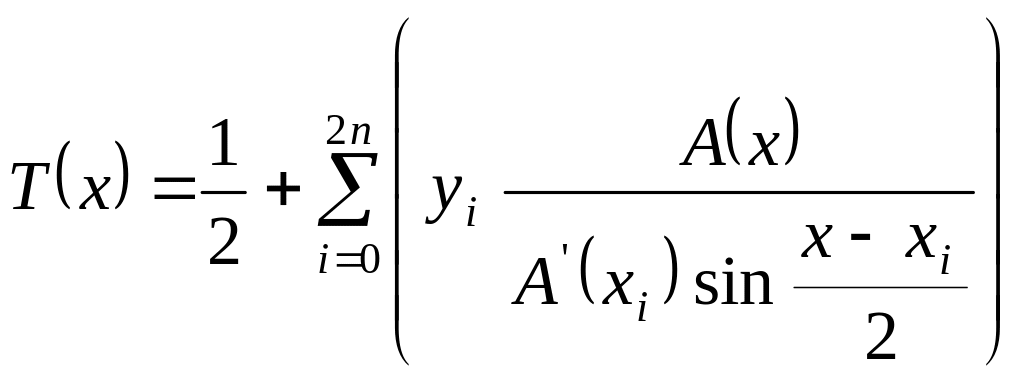 ,
,
где
![]() .
.
Выражение существенно упрощается в случае равноотстоящих узлов
![]() .
.
Именно:
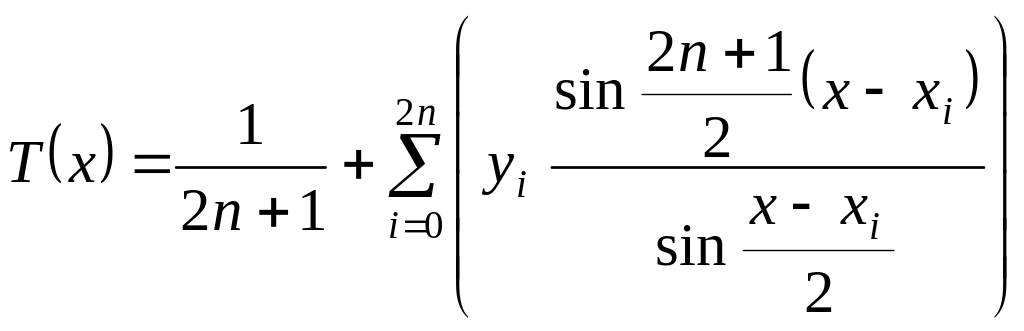 .
.
Для чётных
![]() периодических
функций интерполяционный многочлен
имеет вид
периодических
функций интерполяционный многочлен
имеет вид
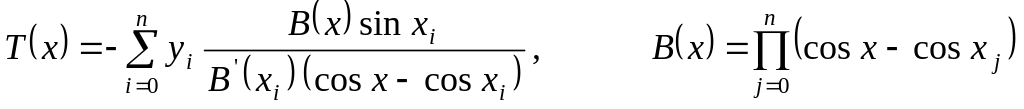 .
.
Для нечётных периодических функций интерполяционный многочлен имеет вид
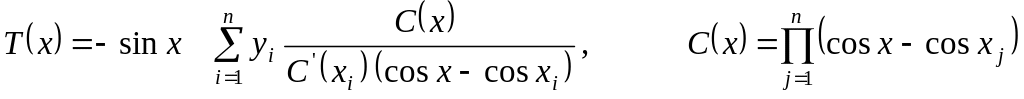 .
.
3.2.21. Ортогональные многочлены
Свойство ортогональности многочленов
![]() .
.
Если, кроме того,
![]() ,
,
то говорят, что многочлены
![]() образуют отро-нормированную систему.
образуют отро-нормированную систему.
Ортогональные многочлены являются специальными решениями линейных однородных дифференциальных уравнений второго порядка.
3.2.22. Вычисление коэффициентов ортогонального многочлена Лагерра
Коэффициенты ортогонального многочлена Лагерра вычисляются по формуле
![]() .
.
Вычисление значений многочлена Лагерра
![]() по рекуррентной формуле
по рекуррентной формуле
![]() .
.
Многочлены Лагерра. Примеры:
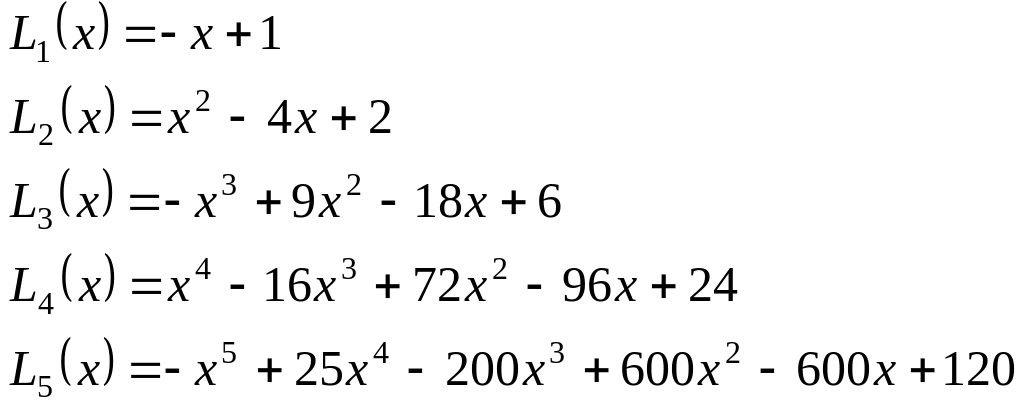
3.2.23. Вычисление коэффициентов ортогонального многочлена Лежандра
Коэффициенты ортогонального многочлена Лежандра вычисляются по формуле
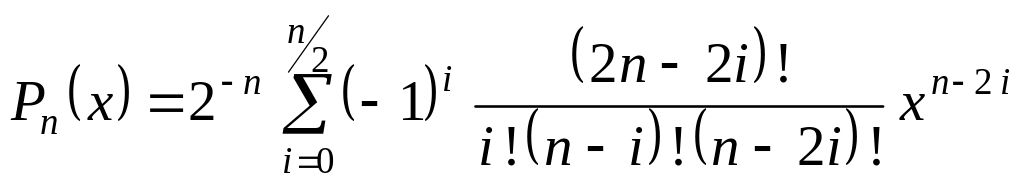 .
.
Пример.
![]() .
.
Вычисление значений многочлена Лежандра
![]() по рекуррентной формуле
по рекуррентной формуле
![]() .
.
Многочлены Лежандра. Примеры:
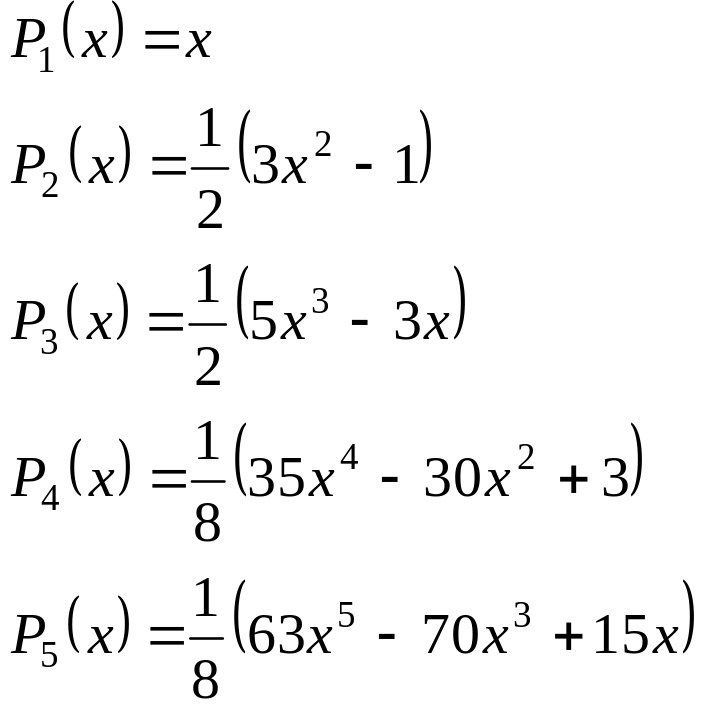
3.2.24. Вычисление коэффициентов ортогональных многочленов Эрмита
Коэффициенты ортогонального многочлена Эрмита вычисляются по формуле
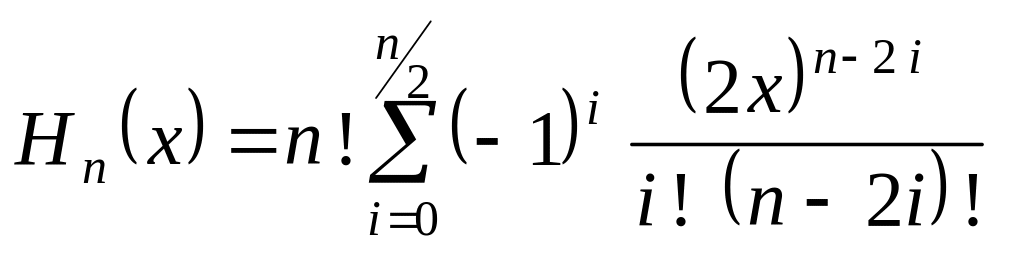 .
.
Пример.
![]() .
.
Вычисление значений многочлена Эрмита
![]() по рекуррентной формуле
по рекуррентной формуле
![]() .
.
Многочлены Эрмита. Примеры:
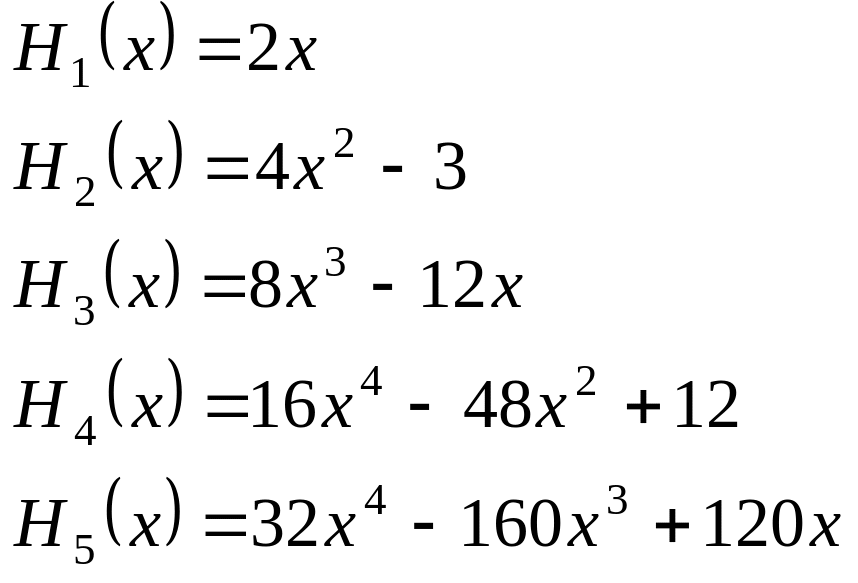
3.2.25. Вычисление коэффициентов ортогональных многочленов Чебышева
Коэффициенты ортогонального многочлена
Чебышева при
![]() вычисляются
по формуле
вычисляются
по формуле
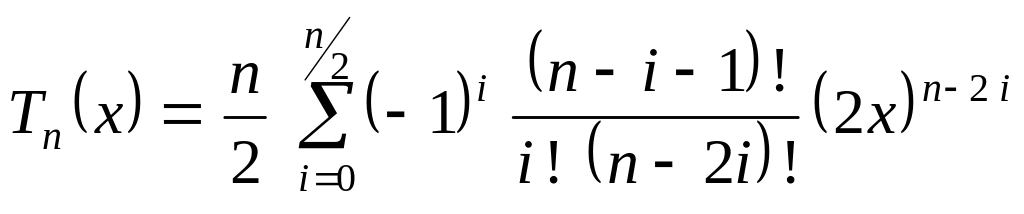 .
.
Пример.
![]() (коэффициенты округляются до целых
чисел).
(коэффициенты округляются до целых
чисел).
Многочлены Чебышева первого рода
![]() и второго рода
и второго рода
![]() вычисляются непосредственно по этим
формулам или по рекуррентным соотношениям
(последние дают меньшую погрешность).
вычисляются непосредственно по этим
формулам или по рекуррентным соотношениям
(последние дают меньшую погрешность).
Вычисление значений многочлена Чебышева
![]() по рекуррентной формуле
по рекуррентной формуле
![]() .
.
Свойства многочленов Чебышева.
При четном (нечетном) многочлен содержит только четные (нечетные) степени .
Старший коэффициент многочлена при
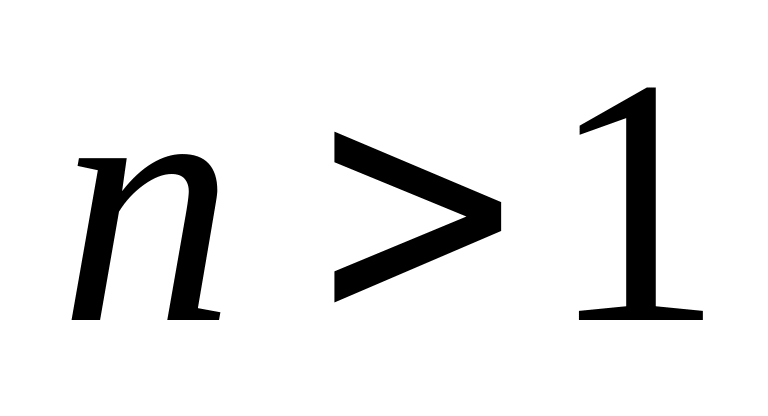 равен
равен
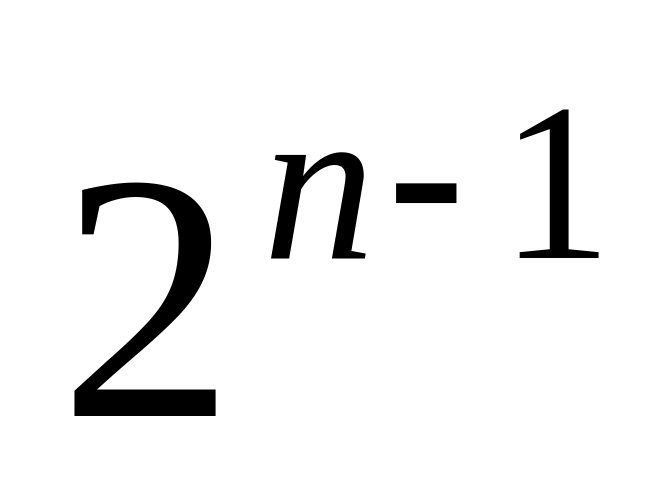 .
.имеет действительных корней в интервале
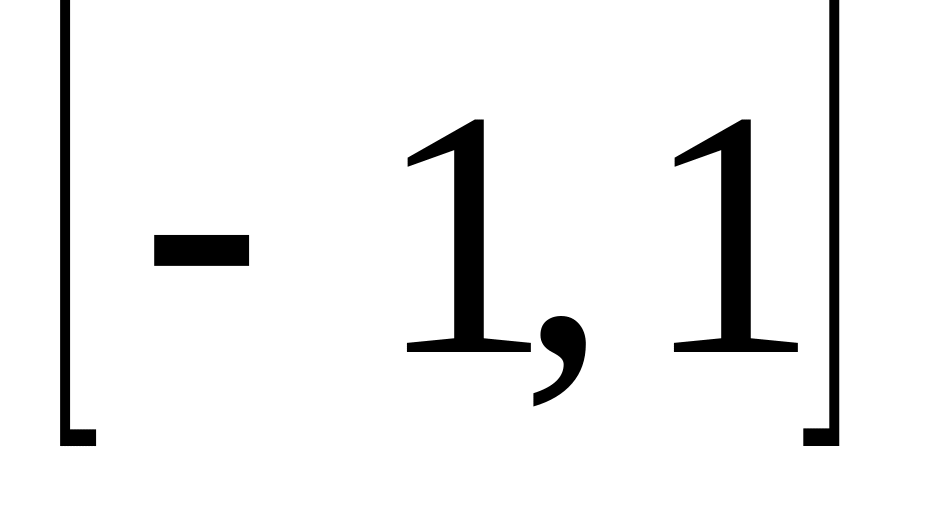 ,
выражаемых формулой
,
выражаемых формулой
![]() .
.
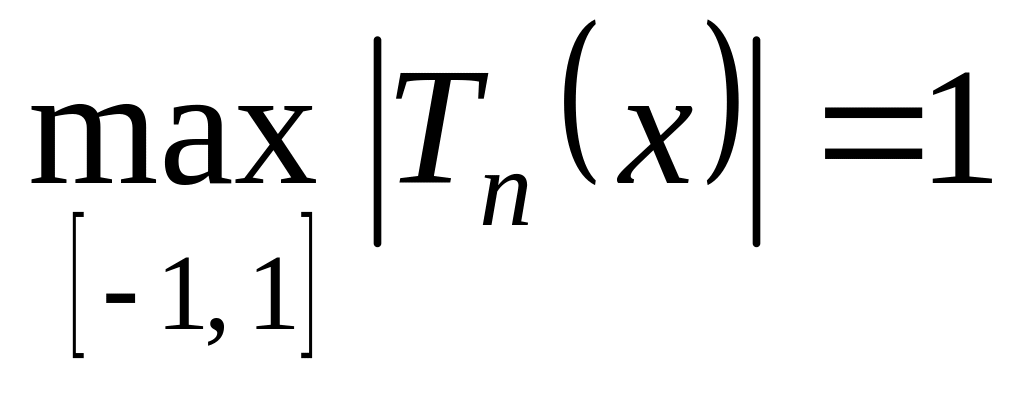 ,
причем
,
причем
![]() ,
,
где
![]() .
.
Многочлен
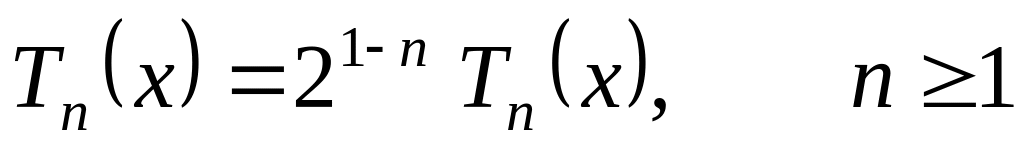 ,
,
среди всех многочленов й степени со старшим коэффициентом, равным единице, имеет на отрезке наименьшее значение максимума модуля, т.е. не существует такого многочлена й степени со старшим коэффициентом, равным единице, что
![]()
Многочлены Чебышева. Примеры: