Экзаменационные вопросы по дисциплине «Теория вероятностей и математическая статистика»

1. Понятия: «случайное испытание», «достоверное событие», «невозможное событие», «случайное событие».

Случайное испытание - это выполнение некоторого комплекса E условий поведения исследования какого - либо случайного явления.

Достоверное событие- событие, которое неизбежно происходит при каждом осущ-нии комплекса условий проведения исследования, и обозначается символом U.

Невозможное событие - событие не может произойти при реализации комплекса E условий провидения условий, и обозначается символом V.

Случайное событие - событие, которое при осущ - нии комплекса условий, может произойти, а может и не произойти.

2. Понятия: «влечение одного события другим событием», «равносильность событий». Свойство транзитивности отношений между событиями.

Влечение одного события другим событием - если при каждой реализации комплекса Е условий проведения исследования всякий раз, когда происходит событие А, наступает и событие В, то говорят что в данном испытании событие А влечет событие В (событие А яв-ся частным случаем событием В).

Равносильность событий - если в некотором испытании событие А влечет событие В, и вместе с тем событие В влечет событие А, т.е. если при каждой реализации заданного комплекса Е условий проведения исследования оба события или наступают или оба не наступают. Обозначается: А=В, читается "А равносильно В".

Транзитивность отношений между событиями - из формулировок введенных понятий следует, что указанные отношения обладают св-вом переходности: если "А влечет В", "В влечет С", то "А влечет С". Ели "А равносильно В", "В равносильно С", то "А равносильно С".

3. Определения действий над событиями. Понятия: «несовместимые события», «полная группа попарно несовместимых событий».

Несовместимые события - события А,В наз-ся несовместимыми, если наступление одного из этих событий исключает появление в том же испытаний другого события. Очевидно что любые два события, противоположные друг другу, несовместимы.

Полная группа попарно несовместимых событий - события S1,S2,...,Sn образуют по отношению к испытанию полную группу попарно несовместимых событий, если исходом данного испытания всякий раз может быть одно и только одно из этих событий. Кому нужно (При одноразовом бросании класс-кой игральной кости события S1, S2, S3, S4, S5, S6, каждое из которых происходит лишь в случае появления соответствующей грани, составляют полную группу попарно несовместимых событий.)

4. Геометрическая интерпретация действий над событиями с помощью диаграмм Эйлера – Вьенна.

Одним из наглядных представлений случайных событий и операций над ними

являются так называемые диаграммы Виена. Пусть внутри квадрата, изображенного

на рис. 1.1. наудачу выбирается точка, не лежащая ни на одной из нарисованных

окружностей. Обозначим через A и B соответствующий выбор точки в левом и

правом кругах. Области, заштрихованные на рис. 1.1. изображают соответственно

4события A, A, B, B, A + B, AB. По диаграммам Виена легко проверяются правила

сложения и умножения событий.

5. Свойства действий над событиями.

1.А+В=В+А, АВ=ВА – переместительное свойство

2.(А+В)?С=А?С+В?С, А?С+В=(А+В) ?(А+С) – распределительное свойство

3.(А+В)+С = А+(В+С), (АВ) ?С=А?(ВС) – сочетательное свойство

4.А+А=А, А?А=А

Правило двойственности (теорема де Моргана)

Для всякого сложного события, выраженного через сумму и произведение (даже счетного количества) событий, противоположное событие может быть получено путем замены событий им противоположными и замены знака произведения на знак суммы, а знака суммы на знак произведения, при оставлении порядка операций неизменным

6. Понятие «равновозможные события». Классическое определение вероятности, свойства классической вероятности.

В классическом определении вероятности мы находимся в рамках схемы случаев в том смысле, что элементарные события равновозможны, т.е. представляют собой случаи.

Определение. Вероятность P(A) события A равняется отношению числа возможных случаев, благоприпятствующих событию A, к числу всех возможных случав, то есть

P (A)=m\n

Из определения вероятности следует, что для вычисления P(A) требуется прежде всего выяснить, какие события в условиях данной задачи, являются возможными случаями, затем подсчитать число возможных случаев, благоприятствующих событию A, число всех возможных случаев и найти отношение числа благоприятствующих случаев к числу всех возможных.

Рассмотрим некоторые свойства вероятностей, вытекающие из классического

определения.

1. Вероятность достоверного события равна единице. Достоверное событие U

обязательно происходит при испытании, поэтому все возможные случаи являются

для него благоприятствующими и

P (U) = n\n=1

2. Вероятность невозможного события равна нулю. Число

благоприятствующих случаев для невозможного события равна нулю (М=0),

поэтому P (V) = 0\n=0

3. Вероятность события есть число, заключенное между нулем и единицей.

7. Комбинаторный метод установления количеств исходов при классическом определении вероятности.

Формулы комбинаторики позволяют найти общее число неодинаковых результатов случайного испытания, состоящего в выборе наудачу к элементов из S различных элементов исходного множества {е1,е2,...,еs}. Исход такого испытания наз-ся выборкой объема из генеральной сов-ти объема S. Испытание вкл. в себя:

• правило, определяющее положение отобранного элемента по отношению к множеству - источнику (безвозвратная схема)

• правило, позволяющее различать возможные исходы ипытания (возвратная схема).

8. Условная классическая вероятность, свойства условной классической вероятности.

Св-ва класс-кой вероятности:

1. Вероятность любого события А неотрицательная: Р(А)≥0

2. Вероятность достоверного события равна единице: Р(U)=1

3. Теорема сложения вероятностей: вероятность суммы двух событий А, В равна разности суммы вероятностей этих событий и вероятности их произведения: Р(А+В)=Р(А)+Р(В)-Р(АВ) (кому нужно: вероятность А+В равносильно вероятности А + вероятности В - вероятность АВ)

4. Вероятность Р(Ā) события Ā, противоположного события А,и равна 1- Р(А)

5. Вероятность невозможного события равна нулю: Р(V)=0

9. Теорема умножения классических вероятностей для произвольного конечного числа событий.

Теорема умножения вероятностей зависимых событий. Вероятность

совместного наступления двух зависимых событий равна вероятности одного

события, умноженной на условную вероятность другого события при условии, что

первое произошло:

P( A⋅ B) = P(A)⋅ P(B / A) = P(B)⋅ P(A/ B)

Говорят, что событие А независимо от события В, если имеет место

равенство Р(А/В)=Р(А).

Следствие 1. Вероятность совместного наступления двух независимых

событий равна произведению вероятностей этих событий (теорема умножения для

независимых событий):

m(A*e)=m(A)*m(e)

Следствие 2. Вероятность суммы двух событий равна сумме вероятностей

этих событий без вероятности совместного их наступления (теорема сложения для

любых событий), т.е. если А и В - любые события, совместимые или несовместимые,

то

Р (A + В )= Р(А) + Р(В) − Р(А ⋅В)

Следствие 3. Пусть производится n одинаковых независимых испытаний, при

каждом из которых событие А появляется с вероятностью р. Тогда вероятность

появления события А хотя бы один раз при этих испытаниях равна 1-(1-р)ⁿ

10. Понятия: «стохастическая независимость одного случайного события от другого», «стохастическая независимость случайных событий в совокупности».

События А и В называются стохастически независимыми между собой, если вероятность произведения данных событий равна произведению их вероятностей Р(АВ)=Р(А)*Р(В), в противном случае события А,В называются стохастически независимыми

11. Формула полной вероятности. Формула Бейеса.

Рассмотрим полную группу n попарно несовместимых событий A1,A2,...,An,

то есть

12. Статистическое определение вероятности, предпосылки статистического метода расчета вероятности, свойства статистической вероятности.

Следует отметить, что классическое определение вероятности имеет

существенный недостаток, заключающийся в том, что в практических задачах не

всегда можно найти разумный способ выделения “равносильных случаев”.

Из-за указанного недостатка наряду с классическим пользуются

статистическим определением вероятности, опирающимся на понятие частоты (или

частости).

Если классическое определение вероятности исходит из соображений

равновозможности событий при некоторых испытаниях, то статистически

вероятность определяется из опыта, наблюдения результатов испытания.

Назовем число m появления события А при n испытаниях частотой, а

Отношение m\n - частостью (относительной частотой) события.

Определение 1.9. Статистической вероятностью события считают его относительную частоту или число, близкое к ней.

Замечание 1. Из формулы (1.2) следует, что свойства вероятности, доказанные для ее классического определения, справедливы и для статистического определения вероят-ности.

Замечание 2. Для существования статистической вероятности события А требуется:

1)      возможность производить неограниченное число испытаний;

2)      устойчивость относительных частот появления А в различных сериях достаточно большого числа опытов.

К недостаткам статистического определения вероятности следует отнести то,

что оно носит описательный, а не формально-математический характер; кроме того,

такое определение не показывает реальных условий, при которых наблюдается

устойчивость частот.

13. Понятие «последовательность независимых повторных испытаний». Вероятностная схема Бернулли. Формула Бернулли. Наиболее вероятное число появлений наблюдаемого события.

При решении вероятностных задач часто приходится сталкиваться с

ситуациями, в которых одно и тоже испытание (опыт) испытания повторяется

многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли..

Поставим задачу общем виде. Пусть в результате испытания возможны два

исхода: либо появится событие А, либо противоположное ему событие A. Проведем

n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность

появления события А в каждом отдельно взятом или единичном испытании

постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в

одинаковых условиях). Обозначим вероятность Р(А) появления события А

единичном испытании буквой р, т.е. Р(А) = р, а вероятность Р(A) - буквой q, т.е.

Р(A) = 1- P (A ) = 1-p = q.

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

(формула)

14. Локальная теорема Муавра-Лапласа. Локальная асимптотическая формула Муавра-Лапласа.

Пусть производится n одинаковых независимых испытаний с вероятностью

появления события в каждом испытании, равной p. Тогда вероятность частоты m

наступления события А определяется, как было показано ранее по формуле

Бернулли:

Вычисление по этой формуле трудно практически осуществить при n>20.

Муавром и Лапласом была получена асимптотическая формула, позволяющая

найти указанную вероятность. Теорема, выражающая эту формулу, носит название

локальной теоремы Муавра-Лапласа .

Эта теорема дает приближение биномиального закона распределения к

нормальному при n → ∞ и p, значительно отличающемся от нуля и единицы. Для

практических расчетов удобнее представлять полученную формулу в виде

15. Интегральная теорема Муавра-Лапласа. Интегральная асимптотическая формула Муавра-Лапласа. Свойства функции Лапласа.

Для вычисления вероятности того, что частота m, подчиненная

биномиальному закону распределения, заключена между данными значениями m1 и

m2, применяют интегральную теорему Лапласа, выраженную асимптотической

формулой

16. Закон больших чисел. Теорема Бернулли.

Следовательно одной из основных задач теории вероятностей является

установление закономерностей, происходящих с вероятностями близкими к единице.

Эти закономерности должны учитывать совместное влияние большого числа

независимо (или слабо зависимо) действующих факторов. При этом каждый фактор

в отдельности характеризуется незначительным воздействием. Всякое предложение,

устанавливающее отмеченные выше закономерности, называется законом больших

чисел. Законом больших чисел, по определению проф. А.Я.Хиничина, следует

назвать общий принцип, в силу которого совокупное действие большого числа

факторов приводит при некоторых весьма общих условиях к результату, почти не

зависящему от случая.

Теорема Бернулли. Пусть производится n независимых испытаний, в

каждом из которых вероятность появления события постоянна и равна р. Тогда

каково бы ни было ε>0,

()

17. Теорема Пуассона. Асимптотическая формула Пуассона.

Теорема Пуассона. Если в последовательности независимых испытаний

появление события А в К-ом испытании равна рк, то

()

где m есть случайная величина, равная числу появлений событя А в первых n

испытаниях.

18. Понятие «случайная величина». Интегральная функция распределения случайной величины, свойства интегральной функции распределения.

 Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента - случайноесобытие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина.Случайная величина является одним из центральных понятий теории вероятностей.

Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело сдискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямойI=[100, 3000]).

Каждая случайная величина полностью определяется своей функцией распределения.  Интегральной функцией распределения называют функцию F(x), определяющую для каждого значения x случайной величиныX вероятность того, что величина X примет значение, меньшее x, то есть F(x) = P(X < x).

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.

Функция распределения любой случайной величины обладает следующими свойствами:

• F(x) определена на всей числовой прямой R;

• F(x) не убывает, т.е. если x₁ x₂, то F(x₁)  F(x₂);

• F(- )=0, F(+ )=1, т.е.

• F(x) непрерывна справа, т.е.

19. Дискретная случайная величина. Ряд распределения, функция распределения дискретной случайной величины.

Случайная величина называется дискретной, если она принимает конечное

или счетное число значений. Дискретная случайная величина задается с помощью

ряда распределения - функции, ставящей в соответствие каждому возможному

значению случайной величины определенную вероятность. Таким образом, ряд

распределения - это конечное или счетное множество пар элементов:

{xi, pi }, i=1,2, ... ; pi=P(X= xi) .

Ряд распределения удобно изображать в виде таблицы:

?x ...? x2 ... xi X =? 1 ?, ? p1 p2 ... pi ...?

в верхней строке которой указаны возможные значения xi дискретной случайной

величины X , а в нижней - соответственно вероятности того, что X примет значение

xi

20. Плотность распределения случайной величины, свойства плотности распределения. Понятие «непрерывная случайная величина».

Перейдем теперь к понятию непрерывной случайной величины.

Непрерывная случайная величина принимает возможные значения,

заполняющие сплошь заданный интервал, причем для любого x из этого интервала

существует предел:

()

Функция p(x) /иногда обозначаемая через f(x) / называется плотностью

распределения /дифференциальным законом распределения/. Из приведенного

определения вытекают следующие свойства плотности распределения:

1. p( х) ≥ 0

2. 2. При любых x1 и x2, входящих в заданный интервал, удовлетворяет равенству

()

3. 

Заметим, что для удобства изучения непрерывных случайных величин

плотность распределения определяют не на конечном интервале возможных

значений случайной величины, а на всей действительной числовой прямой, полагая,

естественно, p(x) тождественно равной нулю для x , лежащих вне интервала

возможных значений случайной величины.

21. Математическое ожидание случайной величины, свойства математического ожидания.

 Математическим ожиданием случайной величины Х называется число

т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям соответствующих элементарных событий.

 Пусть случайная величина Х принимает значения х₁, х₂,…, х_m. Тогда справедливо равенство

т.е. математическое ожидание случайной величины – это взвешенная сумма значений случайной величины с весами, равными вероятностям того, что случайная величина принимает определенные значения.

Основные свойства математического ожидания:

1. математическое ожидание константы равно этой константе, Mc=c ;

2. математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин  ,  и произвольных постоянных a и bсправедливо: M(a + b ) = a M( )+ b M( );

3. математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(  ) = M( )M( ).

22. Дисперсия случайной величины, свойства дисперсии. Среднее квадратическое отклонение случайной величины.

Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.

Если случайная величина  имеет математическое ожидание M , то дисперсией случайной величины  называется величина D = M( - M )².

Легко показать, что D = M( - M )²= M ² - M( )².

Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина M ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

Для определения меры разброса значений случайной величины часто используетсясреднеквадратичное отклонение  , связанное с дисперсией  соотношением 

Основные свойства дисперсии:

1. дисперсия любой случайной величины неотрицательна, D   0;

2. дисперсия константы равна нулю, Dc=0;

3. для произвольной константы D(c ) = c²D( );

4. дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(  ) = D( ) + D ( ).

23. Начальные и центральные моменты случайной величины. Формулы для расчетов начальных и центральных моментов дискретных и непрерывных случайных величин.

В теории вероятностей и математической статистике, помимо математического ожидания и дисперсии, используются и другие числовые характеристики случайных величин. В первую очередь это начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины  называется математическое ожидание k-й степени случайной величины  , т.е.  _k = M ^k.

Центральным моментом k-го порядка случайной величины  называется величина  _k, определяемая формулой  _k = M( - M )^k.

Заметим, что математическое ожидание случайной величины - начальный момент первого порядка,  ₁ = M , а дисперсия - центральный момент второго порядка,

 ₂ = M ² = M( - M )² = D .

Существуют формулы, позволяющие выразить центральные моменты случайной величины через ее начальные моменты, например:

 ₂= ₂- ₁²,  ₃ =  ₃ - 3 _2 1 + 2 ₁³.

Если плотность распределения вероятностей непрерывной случайной величины симметрична относительно прямой x = M , то все ее центральные моменты нечетного порядка равны нулю.

24. Характеристики формы кривой распределения случайной величины: коэффициент асимметрии, эксцесс.

если кривая распределения p(x) непрерывной

случайной величины X симметрично расположена относительно оси, проходящей

через M(X), то все центральные моменты нечетного порядка равны нулю. То же

самое заключение можно сделать по поводу дискретной случайной величины X,

если ее полигон симметричен относительно оси, проходящей через среднее значение

случайной величины.

Нормальное распределение наиболее часто используется в теории вероятностей и в математической статистике, поэтому график плотности вероятностей нормального распределения стал своего рода эталоном, с которым сравнивают другие распределения. Одним из параметров, определяющих отличие распределения случайной величины  , от нормального распределения, является эксцесс.

Эксцесс  случайной величины  определяется равенством  .

У нормального распределения, естественно,  = 0. Если  ( ) > 0, то это означает, что график плотности вероятностей p_ (x) сильнее “заострен”, чем у нормального распределения, если же ( ) < 0, то “заостренность” графика p_ (x) меньше, чем у нормального распределения.

Асимметрия

В теории вероятностей и в математической статистике в качестве меры асимметрии распределения является коэффициент асимметрии, который определяется формулой  ,

где  ₃ - центральный момент третьего порядка,  - среднеквадратичное отклонение.

25. Биномиальное распределение, числовые характеристики распределения.

Биноминальное распределение представляет собой распределение

вероятностей возможных чисел появления события А при n независимых испытаний,

в каждом из которых событие А может осуществиться с одной и той же

вероятностью P(A) = p = const. Кроме события A может произойти также

противоположное событие A , вероятность которого P( A ) = 1-p = q.

Числовые характеристики биноминального распределения:

M(m)=np - математическое ожидание частоты появлений события A при n

независимых испытаниях;

D(m)=npq - дисперсия частоты появления события A;

σ(m ) = под корнем n p q - среднее квадратическое отклонение частоты.

26. Распределение Пуассона, числовые характеристики распределения.

Теперь рассмотрим, как изменится биномиальный закон в случае, когда p ≠ q, то есть p –> 0. В этом случае применить гипотезу о нормальности распределения нельзя, и биномиальное распределение переходит в распределение Пуассона.

Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и приp –> 0 (редкие события)).

Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:

где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию.

Одной из основных числовых характеристик СВ X, распределенной по закону Пуассона, является математическое ожидание:

После некоторых преобразовании [3]  получим:  mx = а. Таким образом, параметр апредставляет собой не что иное, как математическое ожидание СВ X.

Другая числовая характеристика – дисперсия, которая тоже равна параметру а, т. е. Дх = а.

Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а:

mx =Дх = a 

27. Равномерное распределение, числовые характеристики распределения.

Говорят, что случайная величина   имеет равномерноераспределение на отрезке [a,b], если она непрерывна, принимает значения только на отрезке [a,b], а плотность ее распределения постоянна на отрезке [a,b], и равна 0 вне этого отрезка.

Если переменная х лежит между нижним пределом а и верхним пределом b, при равномерном распределении частота распределения задается формулой f(x)=1/(b–а) для а ≤ х ≤ b и для f(x)=0 для х<а и x>b.

28. Нормальное распределение. Свойства распределения. Правило трёх сигм. Примеры полезных статистик, имеющих нормальное распределение.

Нормальное распределение - наиболее часто встречающийся вид

распределения. С ним приходится сталкиваться при анализе погрешностей

измерений, контроле технологических процессов и режимов, а также при анализе и

прогнозировании различных явлений в в экономике, социологии, демографии и

других областях знаний.

Наиболее важным условием возникновения нормального распределения

является формирование признака как суммы большого числа взаимно независимых

слагаемых, ни одно из которых не характеризуется исключительно большой по

сравнению с другими дисперсией. В производственных условиях такие предпосылки

в основном соблюдаются.

Главная особенность нормального распределения состоит в том, что оно

является предельным, к которому приближаются другие распределения.

Легко показать, что функция Ф(х) (интеграл вероятностей) обладает следующими свойствами.     1°. Ф(0)=0     2°.  ; при   величина   практически равна 1/2     3°. Ф(-x)=-Ф(х), т.е. интеграл вероятностей является нечетной функцией. 

Правило трёх сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале  . Более строго — не менее чем с 99,7 % достоверностью значение нормально распределенной случайной величины лежит в указанном интервале (при условии, что величина   истинная, а не полученная в результате обработки выборки).

Если же истинная величина   неизвестна, то следует пользоваться не  , а s. Таким образом, правило трёх сигм преобразуется в правило трёх s.

Разнообразные статистические данные с хорошей степенью точности можно считать реализациями случайной величины, имеющей нормальное распределение. 

29. Понятие «многомерная случайная величина». Интегральная функция распределения многомерной случайной величины, свойства многомерной функции распределения (на примере двумерной случайной величины).

Многомерной случайной величиной называется величина, которая при проведении опыта принимает в качестве своего значения не число, а целый набор чисел, заранее не известно каких. Эти наборы, которые случайная величина может принять, образуют множество ее возможных значений. Таким образом, хотя конкретный набор не предугадаешь, он будет из множества возможных наборов (часто это множество хорошо известно).

Свойства совместной функции распределения двумерной случайной величины

1. Значения совместной функции распределения удовлетворяют двойному неравенству:

.

2.   – неубывающая функция по каждому аргументу, т.е.

, если  ;

, если  .

3. Совместная функция распределения имеет следующие предельные значения:

;

;

;

.

4. При   совместная функция распределения системы становится функцией распределения составляющей  :

;

при   совместная функция распределения системы становится функцией распределения составляющей  :

.

30. Плотность распределения многомерной случайной величины, свойства многомерной плотности распределения (на примере двумерной случайной величины).

Плотность распределения, плотность вероятности , плотность распределения вероятности втеории вероятностей — производная абсолютно непрерывной функции распределения.

Пусть ξ — случайная величина с функцией распределения F(x); пусть существует неотрицательная функцияf(x) такая, что для любых 

тогда   называется плотностью распределения случайной величины ξ.

Для любого борелевского множества 

Любая неотрицательная интегрируемая функция f(x), удовлетворяющая условию номировки

является плотностью распределения некоторой случайной величины ξ.

Плотность многомерного распределения случайного вектора   определяется как функция многих переменных   такая, что

где F — абсолютно непрерывная функция многомерного распределения случайного вектора ξ.

Свойства: (фотка)

http://alexandr4784.narod.ru/B16/b16_5_53.pdf

31. Условные числовые характеристики случайной величины.

Условные числовые характеристики

 

Рассмотрим условные числовые характеристикизависимых случайных величин.  Условное математическое ожидание:

.

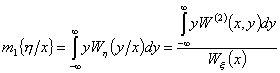Условная дисперсия:

 

Так, для нормальных величин   и    имеем:

 

 

Очевидно, что при   условные моменты совпадают с безусловными:

 

Однако при                    

32. Понятие «стохастическая независимость случайных величин в совокупности».

Стохастической связью между случайными величинами называется такая связь, при которой с изменением одной величины меняется распределение другой. Функциональной зависимостью называется такая связь между случайными величинами, при которой при известном значении одной из величин можно точно указать значение другой.

В отличие от функциональной связи при стохастической связи с изменением величины Х величина Y имеет лишь тенденцию изменяться. По мере увеличения тесноты стохастической зависимости она все более приближается к функциональной, а в пределе ей соответствует. Крайняя противоположность функциональной связи — полная независимость случайных величин.

Если случайные величины независимы, то согласно теореме умножения (7.10–7.11) получаем

         и  ,        (7.14)

        .        (7.15)

Условие (7.15) можно использовать в качестве необходимого и достаточного критерия независимости двух случайных величин, если известны плотности распределения системы и случайных величин, в нее входящих.

33. Ковариация случайных величин, свойства ковариации.

Если между случайными величинами  и  существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( ,  ). Ковариацию вычисляют по формулам cov( ,  )=M[( - M )( - M )]  M( ) - M M .

Если случайные величины  и  независимы, то cov( , )=0.

Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.

Свойства ковариации:

cov( ,  ) = D ;

 

;

;

,

где C₁ и C₂ - произвольные константы.

Ковариационной матрицей случайного вектора ( , ) называется матрица вида

.

Эта матрица симметрична и положительно определена. Ее определитель называетсяобобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( , ).

Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий:  . Если же случайные величины зависимы, то  .

34. Коэффициент корреляции случайных величин, свойства коэффициента корреляции.

Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции  .

Этот коэффициент обладает следующими свойствами:

он безразмерен;

его модуль не превосходит единицы, т.е.  ;

если x и h независимы, то k(x ,h )=0 (обратное неверно!);

если  , то случайные величины x и h связаны функциональной зависимостью вида

h = ax +b,

где a и b- некоторые числовые коэффициенты;

;

Корреляционной матрицей случайного вектора называется матрица

.

Если   и  , то ковариационная и корреляционная матрицы случайного вектора (x ,h ) связаны соотношением  , где  .

35. Неравенство Маркова, неравенство Чебышёва.

Формулировка неравенства Маркова

Если среди значений случайной величины Х нет отрицательных, то вероятность того, что она примет какое-нибудь значение, превосходящее положительное число А, не больше дроби  , т.е.

,                                    

а вероятность того, что она примет какое-нибудь значение, не превосходящее положительного числа А, не меньше  , т.е.

.      

Чебышева.

Вероятность того, что отклонение случайной величины Х от ее

математического ожидания по абсолютной величине меньше положительного числа

ε, не меньше, чем   , т.е.

.                                 

36. Закон больших чисел. Теорема Чебышёва.

Формулировка теоремы Чебышева

Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а₁, а₂, …, а_n не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.

Следствие.

Если независимые случайные величины имеют одинаковые, равные , математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е.

При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:

,          

.        

Из теоремы Чебышева следует утверждение, заключающиеся в том, что

среднее арифметическое достаточно большого числа независимых случайных

величин, имеющих ограниченные дисперсии, утрачивает случайный характер и

становится детерминированной величиной.

37. Центральная предельная теорема. Теорема Ляпунова.

Теорема Ляпунова. Рассмотрим n независимых случайных величин Х1,

Х2,…,Хn, удовлетворяющих условиям:

1) все величины имеют определенные математические ожидания и конечные

дисперсии;

2) ни одна из величин не выделяется резко от остальных по своим значениям.

Тогда при неограниченном возрастании n распределение случайной величины () приближается к нормальному закону

()

38. Понятия: «генеральная совокупность», «выборочная совокупность». Сущность выборочного метода.

Генеральная совокупность:

Множество всех возможных как реально существующих так и домысливаемых объектов, обусловленных комплексом условий наблюдений над значениями одного или нескольких признаков объектов.

Выборочная совокупность:

Часть(подмножество) объектов генеральной совокупности, отобранных для изучения

Сущность выборочного метода состоит в вынесении научно-обоснованного суждения об объективных свойствах генеральной совокупности по выборочной совокупности.

39. Выборка. Вариационный ряд. Выборочные характеристики распределения.

Выборка (Выборочная совокупность) Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на всю генеральную совокупность, выборка должна обладать свойством репрезентативности, т.е. правильно отражать пропорции

генеральной совокупности. Это достигается случайностью отбора, когда все объекты

генеральной совокупности имеют одинаковую вероятность быть отобранными.

Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы  ', а вторая - их частоты   (относительные частоты  .

Кроме эмпирической функции распределения, для описания данных используют и другие статистические характеристики. В качестве выборочных средних величин постоянно используют выборочное среднее арифметическое, т.е. сумму значений рассматриваемой величины, полученных по результатам испытания выборки, деленную на ее объем:

где n – объем выборки, x_i – результат измерения (испытания) i-ого элемента выборки.

Кроме перечисленных выше статистических характеристик, в качестве выборочного показателя рассеивания используют размах R – разность между n-й и первой порядковыми статистиками в выборке объема n, т.е. разность между наибольшим и наименьшим значениями в выборке: R = x(n) –x(1).

40. Эмпирическая функция распределения, свойства данной функции.

Пусть известно статистическое распределение частот количественного признака X. Введем обозначения:

 – число наблюдений, при которых наблюдалось значение признака, меньшее  ;

 – общее число наблюдений (объем выборки).

Ясно, что относительная частота события   равна  .

Если   будет изменяться, то будет изменяться и относительная частота, то есть относительная частота  есть функция от  .

Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию  , определяющую для каждого значения   относительную частоту события  .

Итак, по определению  , где   – число вариант, меньших  ,   – объем выборки.

Из определения функции  вытекают следующие ее свойства:

1) значения эмпирической функции принадлежат отрезку 

;

2)   – неубывающая функция;

3) если   – наименьшая варианта, то  , при  ;

 если   – наибольшая варианта, то   при  .

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

41. Точечная оценка неизвестного параметра (или числовой характеристики) распределения. Понятия состоятельности и несмещенности точечной оценки.

Точечной оценкой называют некоторую функцию результатов наблюдения

θn(x1, x2, ... , xn), значение которой принимается за наиболее приближенное в данных

условиях к значению параметра θ генеральной совокупности.

Примером точечных оценок являются X , S2, S и др., т.е. оценки параметров

одним числом.

Из точечных оценок в приложениях математической статистики часто

используют начальные

()

И центр-е

()

моменты до четвертого порядка включительно, т.е. k=1,2,3,4

Точечную оценку называют несмещенной, если ее математическое

ожидание равно оцениваемому параметру:

()

Выполнение требования несмещенности оценки гарантирует отсутствие

ошибок в оценке параметра одного знака.

Точечная оценка параметра θ называется состоятельной, если при n → ∞

оценка сходится по вероятности к оцениваемому параметру, т.е. выполняется

условие

()

Следует отметить, что при состоятельности оценки оправдывается увеличение

объема наблюдений, так как при этом становится маловероятным допущение

значительных ошибок при оценивании.

42. Сравнение точечных оценок. Понятие эффективной точечной оценки.

Основная проблема точечной оценки заключается в выборе возможно лучшей

оценки, отвечающей требованиям несмещенности, эффективности и

состоятельности.

Эффективной называют несмещенную выборочную оценку, обладающую

наименьшей дисперсией среди всех возможных несмещенных оценок параметра θ

для данного объема выборки n и функции распределения вероятности F(X,θ)

генеральной совокупности.

43. Методы определения точечных оценок параметров распределения: метод моментов Пирсона, метод максимального правдоподобия Фишера.

Метод предложен Р. Фишером в 1912 г. Метод основан на исследовании вероятности получения выборки наблюдений (x1, x2, …, xn). Эта вероятность равнаf(х1, T) f(х2, T) … f(хп, T) dx1 dx2 … dxn.

Совместная плотность вероятности

L(х1, х2 …, хn ; T) = f(х1, T) f(х2, T) … f(хn, T),

рассматриваемая как функция параметра T, называется функцией правдоподобия.

Итак, нахождение оценок максимального правдоподобия включает следующие этапы: построение функции правдоподобия (ее натурального логарифма); дифференцирование функции по искомым параметрам и составление системы уравнений; решение системы уравнений для нахождения оценок; определение второй производной функции, проверку ее знака в точке оптимума первой производной и формирование выводов.

Метод максимального правдоподобия позволяет получить состоятельные, эффективные (если таковые существуют, то полученное решение даст эффективные оценки), достаточные, асимптотически нормально распределенные оценки. Этот метод может давать как смещенные, так и несмещенные оценки. Смещение удается устранить введением поправок. Метод особенно полезен при малых выборках. Оценка инвариантна относительно преобразования параметра, т.е. оценка некоторой функции  (Т) от параметра Т является эта же функция от оценки  ( ). Если функция максимального правдоподобия имеет несколько максимумов, то из них выбирают глобальный.

Метод предложен К. Пирсоном в 1894 г. Сущность метода:

выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения. Желательно применять моменты младших порядков, так как погрешности вычисления оценок резко возрастают с увеличением порядка момента;

вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам;

параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение этой системы дает оценки параметров распределения генеральной совокупности.

Метод моментов позволяет получить состоятельные, достаточные оценки, они при довольно общих условиях распределены асимптотически нормально. Смещение удается устранить введением поправок. Эффективность оценок невысокая, т.е. даже при больших объемах выборок дисперсия оценок относительно велика (за исключением нормального распределения, для которого метод моментов дает эффективные оценки). В реализации метод моментов проще метода максимального правдоподобия. Напомним, что метод целесообразно применять для оценки не более чем четырех параметров, так как точность выборочных моментов резко падает с увеличением их порядка.

44. χ²-распределение (Пирсона), числовые характеристики этого распределения.

Распределение Пирсона   (хи - квадрат) – распределение случайной величины

где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных

45. Распределение Стьюдента, числовые характеристики этого распределения.

Распределение t Стьюдента – это распределение случайной величины

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. английским статистиком В. Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В. Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В. Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.

В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.

46. Распределение Фишера-Снедекора, числовые характеристики этого распределения.

Распределение Фишера – это распределение случайной величины

где случайные величины Х₁ и Х₂ независимы и имеют распределения хи – квадрат с числом степеней свободы k₁ и k₂ соответственно. При этом пара (k₁, k₂) – пара «чисел степеней свободы» распределения Фишера, а именно, k₁ – число степеней свободы числителя, а k₂ – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.

Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики

47. Основные таблицы математической статистики.

Статистическая таблица — система строк и столбцов, в которой в определенной последовательности излагается статистическая информация о социально-экономических явлениях.

Стандартный нормальный закон

Квантили хи-квадрат распределения

Квантили распределения Стьюдента

В книгу известных ученых включены широко распространенные таблицы (статистика Колмогорова-Смирнова, функция мощности F-критерия и др.), а также таблицы, мало известные советскому читателю (статистика Манна-Уитни, Крускала-Уоллиса и др.), позволяющие использовать непараметрические методы статистики.

Виды статистических таблиц весьма многообразны, что объясняется многообразием массовых явлений и процессов, которые изучает статистика. Таблицы различаются по построению подлежащего, разработке сказуемого и по целям исследования. В зависимости от построения подлежащего статистические таблицы подразделяются на три вида: простые, групповые, и комбинированные. А) Простыми называются такие статистические таблицы, в подлежащих которых имеется только перечень показателей, раскрывающих содержание подлежащего и нет группировок их. Иногда такие таблицы называются перечневыми, или простыми Б) Групповыми называются такие статистические таблицы, в которых изучаемый объект разделен в подлежащем на группы по тому или иному признаку. В) Комбинационной таблицей называется такая таблица, в которой в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации( изучаемый объект разбит на группы), а внутри групп на подгруппы. Например, студенты ВУЗа по факультетам, группам, специальностям). Простые таблицы имеют относительный характер, групповые и комбинационные позволяют передать глубокий анализ изучаемой совокупности. Групповые таблицы дают возможность изучить влияние одного признака на изменение другого признака, а комбинационные на влияние определенного фактора на признаки сказуемого.

48. Понятие «доверительный интервал».

Доверительным интервалом называется интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью α.

Для оценки математического ожидания   случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении   служит доверительный интервал

где   - точность оценки,   - объем выборки,   - выборочное среднее,   - аргумент функции Лапласа, при котором 

49. Доверительный интервал для математического ожидания (генеральной средней) нормального распределения при известной и неизвестной дисперсии.

Существуют два основных метода построения доверительных интервалов: байесовский метод и метод доверительных интервалов, предложенный Нейманом. Рассмотрим примеры построения доверительных интервалов в ряде случаев.