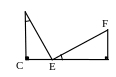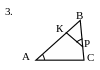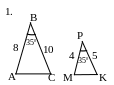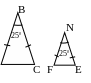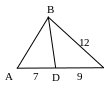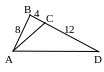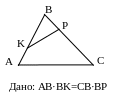4 . Способы получения подобных треугольников

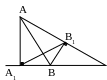
4.1. А₁С₁׀׀АС: ∆А₁ВС₁~∆АВС. 4.2. ∆АВС – остроугольный,

АА₁ ВС, СС₁ АВ: ∆А₁ВС₁~∆АВС с коэффициентом подобия k=cosB.

I.2. Доказательства утверждений теоретической карты №1

Доказательства признаков подобия треугольников приводятся в учебнике [4, стр. 137-138], в учебнике [9, cтр. 176-180]. Докажем утверждения 3.1–3.7.

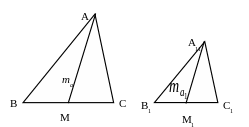
3.1.

Рис. 4

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: длины медиан ∆А₁В₁С₁и ∆АВС.

Доказательство

∆А₁В₁М₁~∆АВМ по второму признаку, так как из подобия треугольников ∆А₁В₁С₁ и ∆АВС следует, что и . Тогда , то есть

3 .2.

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: где - длины высот ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁В₁H₁~∆АВН по первому признаку, так как из подобия треугольников ∆А₁В₁С₁ и ∆АВС следует, что , а Тогда

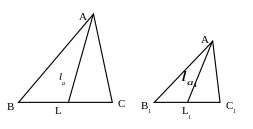3 .3.

Рис. 6

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: где – длины биссектрис ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁В₁L₁~∆АВL по первому признаку, так как из подобия треугольников А₁В₁С₁ и АВС следует, что , а по определению биссектрисы, что Тогда

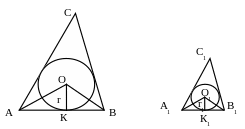3 .4.

Рис. 7

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: где r₁, r – длины радиусов окружностей, вписанных в ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁О₁В₁~∆АОВ по первому признаку, так как из подобия треугольников А₁В₁С₁ и АВС следует, что , а А₁О₁, АО и В₁О₁, ВО – биссектрисы углов А₁ и А, В₁ и В соответственно (центры О₁ и О окружностей, вписанных в ∆А₁В₁С₁ и ∆АВС, - точки пересечения биссектрис). Тогда согласно пункту 3.2

3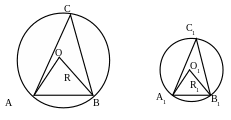 .5.

Рис. 8

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: , где R₁, R длины радиусов окружностей, описанных около ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁О₁В₁~∆АОВ по первому признаку, так как из подобия ∆А₁В₁С₁ и ∆АВС следует, что Треугольники ∆А₁О₁В₁ и ∆АОВ – равнобедренные (А₁О₁=О₁В₁=R₁, АО=ОВ=R), следовательно, Тогда

3.6.

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: , где Р₁ и Р – периметры ∆А₁О₁В₁ и ∆АОВ.

Доказательство

∆А₁В₁С₁~∆АВС с коэффициентом подобия k, следовательно, А₁В₁=k∙АВ, В₁С₁=k∙ВС, А₁С₁=k∙АС. Р₁= А₁В₁+ В₁С₁+ А₁С₁= k∙АВ + k∙ВС + k∙АС=

=k∙(АВ+ВС+АС)=Р. Таким образом,

3.7. Доказательство данного равенства приводится в учебниках [4, стр. 134] и [9, стр.222].

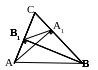
Доказательство того, что в случае 4.1 получается треугольник, подобный данному, тривиально и мы его не приводим. Докажем подобие треугольников в случае 4.2.

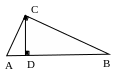
Д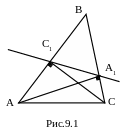 ано: ∆АВС – остроугольный,

АА₁ ВС, СС₁ АВ, А₁С₁ – прямая.

Доказать: ∆А₁ВС₁~∆АВС с коэффициентом подобия k=cosB.

Доказательство

Треугольники АА₁В и СС₁В – прямоугольные, угол В у них общий, следовательно, они подобны по первому признаку. Тогда их стороны

пропорциональны, то есть . В треугольниках А₁ВС₁ и АВС угол В – общий, стороны пропорциональны, следовательно, они подобны по второму признаку. Их коэффициент пропорциональности равен . В прямоугольном треугольнике АА₁В отношение равно косинусу угла В. Таким образом, k = сosB.

Замечание. В процессе доказательства был рассмотрен ещё один способ получения подобных треугольников: проведение двух высот в остроугольном треугольнике. Они «отсекают» подобные треугольники.

АВА₁СВС₁

Задачи к теоретической карте № 1

№1. Найти подобные треугольники и доказать их подобие.

A	К 2. А
B 4. 360 Дано: AB=BC D A C	А D B E C 5.	A C B E D 6.
В 7. 7. АВСD – трапеция.	8.	M F 9.
C 10. В K D A F Дано: ABCD – параллелограмм	A B 11.	12.
13.	A B C D 14. 15.	A B C

Рис. 10

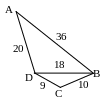
№2. Найти подобные треугольники и доказать их подобие.

	A 2.	N 5 3.
4.	C 5.	6.
B 7. 8. 16 18 12 A C D 24		9.
Д 12. оказать, что ∆A1B1C ~∆ABC и найти коэффициенты подобия.
10.	11.	C

Рис. 11

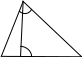
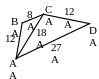
№3. Точка К лежит на стороне АВ треугольника АВО и делит сторону АВ на отрезки ВК=12 и АК=4. Углы ВОК и ВАО равны. Найти площадь треугольника ВОК, если .

П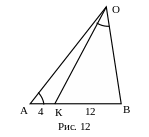 лан решения.

1. ∆ВОК~∆ВАО.

2. ОВ.

3. sin

4. S_∆вок. Ответ: 48.

Используемые факты из теоретической карты: 1; 2.

№4. В треугольнике CEH угол С равен 45⁰, точка Т делит сторону СЕ на отрезки СТ=2, ЕТ=14. Углы CHT и СЕН равны. Найти площадь треугольника СНТ.

Ответ: 4.

№5. В треугольнике АВС АВ=8, ВС=12, АС=16. Точка D делит АС на отрезки AD=7 и DC=9. Найти BD.

П лан решения.

1. ∆ BCD~∆ АСВ.

2. BD.

Ответ: 6.

Используемые факты из теоретической карты: 1; 2; 3.

№6. В треугольнике АВС на медиане ВМ выбрана точка К так, что ÐМКС=ÐВСМ. Доказать, что ÐАКМ=ÐВАМ.

П лан доказательства.

1. ∆МСВ~∆МКС .

2. ; .

3. ∆ABM~∆KAM.

4.

Используемые факты теоретической карты:1; 2.1; 2.2.

№7. В равнобедренном треугольнике с боковой стороной, равной b, проведены биссектрисы углов при основании. Длина отрезка прямой между точками пересечения биссектрис с боковыми сторонами равна m. Определить основание треугольника.

П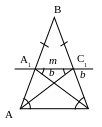 лан решения.

1. А₁С₁|| АС.

2. ∆АС₁А₁: АА₁=А₁С₁=m и

∆ С₁А₁С: А₁С₁=С₁С=m.

3. ∆ С₁ВА₁~∆АВС.

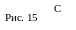4. АС.

Ответ:

Используемые факты теоретической карты: 4.1; 1

№ 8. Основание равнобедренного треугольника равно 8, а боковая сторона 12. Найти длину отрезка, соединяющего точки пересечения биссектрис углов при основании с боковыми сторонами треугольника.

Ответ: 4,8.

№ 9. Дан равнобедренный треугольник с основанием 18 см и высотой 12 см. Отрезок какой длины нужно отложить от вершины треугольника на его боковых сторонах, чтобы соединив их концы, получить трапецию с периметром, равным 40 см?

П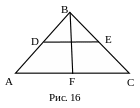 лан решения.

1. АF.

2. AB.

3. Выразить AD через BD.

4. Выразить Р_ADEC через BD и DE.

5. Выразить DE через BD.

6. ∆DBE~∆АВС.

7. BD. Ответ: 10 см.

Используемые факты теоретической карты: 4.1; 1.

№ 10. Доказать, что если между сторонами а, b, и с треугольника АВС существует зависимость а²=b²+bc, то углы А и В, противолежащие сторонам а и b, удовлетворяют равенству ÐА=2 В.

План доказательства.

1.

2. Построить треугольник со сторонами

в+с, а (∆ ВСD).

3. ∆ АВС~∆ ВDC.

4.

5.

Используемые факты теоретической карты: 2.2; 1.

№11. Доказать, что отрезок прямой, лежащий внутри трапеции и проходящий через точку пересечения ее диагоналей параллельно основаниям, делится этой точкой пополам.

П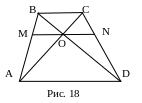 лан доказательства.

1. . 2. . 3. 4. 5. MO=ON.

Используемые факты из теоретической карты: 4.1; 1.

№ 12. В трапеции АВСD проведены диагонали АС и ВD, пересекающиеся в точке F. Из вершины С проведена прямая СК, параллельная боковой стороне AD и пересекающая диагональ DB в точке L, а основание АВ в точке К так, что DF=BL. Найти отношение AB к CD.

П лан решения.

1.

2. 3.

4. 5.

Рис. 19 6. Решить уравнение , где .

Используемые факты из теоретической карты: 2.1; Ответ:

№13. Основания ОК и МР трапеции ОКМР равны 8 и 4 соответственно. Диагонали пересекаются в точке С, а площадь треугольника СМР равна 20. Найти площадь трапеции.

П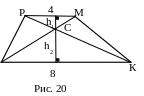 лан решения.

1. h₁. 2. 3. h₂. 4. h₁+h₂.

O

5. S_OKMP. Ответ: 180.

Используемые факты из теоретической карты: 3.2.

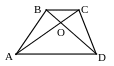
№14. Большее основание трапеции в два раза длиннее ее меньшего основания. Через точку пересечения диагоналей трапеции проведена прямая, параллельная основанию. Найти отношение высот каждой из двух образовавшихся трапеций к высоте данной трапеции.

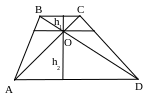План решения.

Пусть высота данной трапеции h.

1. ∆AOD~∆COB.

2. Найти коэффициент подобия.

3. .

Рис. 21 4. и .

Ответ: 1: 3; 2: 3.

Используемые факты из теоретической карты: 3.2; 1.

1 5. В четырехугольнике ABCD сторона АВ равна стороне ВС, диагональ АС равна стороне CD, а угол АВС равен углу АCD. Радиусы окружностей, вписанных в треугольники АВС и ACD, относятся как 3:4. Найти отношение площадей этих треугольников.

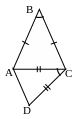План решения.

1. ∆АВС~∆ACD.

2. Найти коэффициент подобия треугольников.

3.

Ответ:

Рис. 22 Используемые факты из теоретической карты: 2.1; 3.7.

№16. В треугольник со сторонами 10 см, 17 см и 21 см вписан прямоугольник с периметром 24 см так, что одна из его сторон лежит на большей стороне треугольника. Найти стороны прямоугольника.

П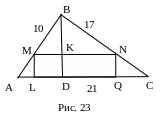 лан решения.

1. Найти высоту треугольника BD.

2. Пусть ML=x. Выразить MN, BK через х.

3. ∆MBN~ ∆ABС.

4. .

5. Найти х.

Ответ: см, см.

Используемые факты из теоретической карты: 4.1; 3.2.

№17. Высота остроугольного треугольника равна 25 см. На каком расстоянии от вершины нужно провести прямую, перпендикулярную этой высоте, чтобы площадь треугольника разделилась пополам?

План решения.

1. ∆А₁ВС₁~∆АВС.

2.Найти коэффициент подобия.

3.ВН₁.

Ответ: см.

Используемые факты из теоретической карты: 4.1; 3.7; 3.2.

№18. Доказать, что радиус окружности, проходящей через середины сторон треугольника, равен половине радиуса окружности, описанной около этого треугольника.

П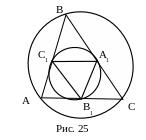 лан доказательства.

1. ∆А₁ВС₁ ~ ∆СВА.

2. Найти коэффициент подобия треугольников.

3. 

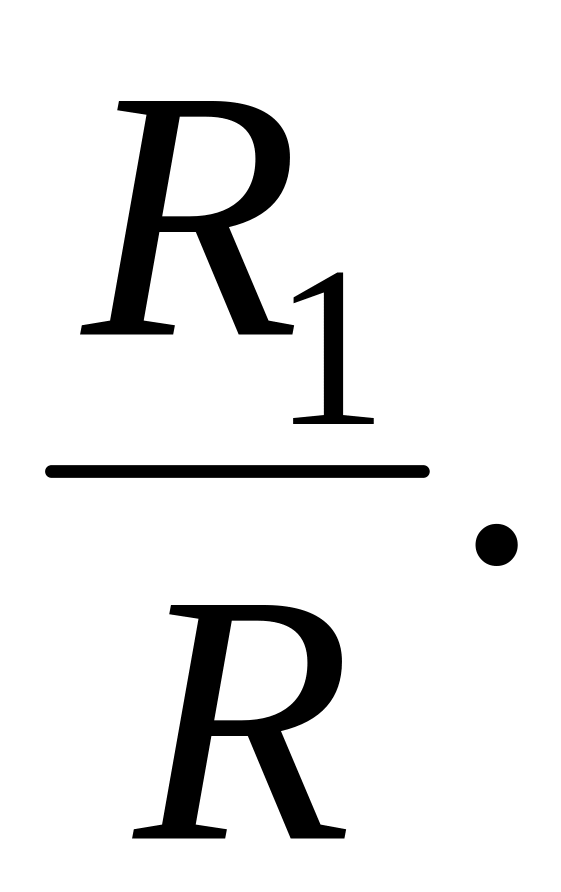
Используемые факты из теоретической карты: 4.1; 3.5.

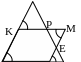
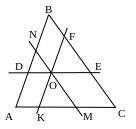№ 19. Внутри треугольника АВС взята произвольная точка О и через нее проведены три прямые, параллельные сторонам треугольника. Эти прямые делят треугольник АВС на шесть частей, три из которых – треугольники. Радиусы окружностей, вписанных в эти треугольники равны , , , радиус окружности, вписанной в треугольник АВС равен . Доказать, что

План доказательства.

1. ∆DNO ~ ∆АВС,

∆OFE ~ ∆АВС,

∆KOM ~ ∆АВС.

2. , , .

3. Сложить равенства (2).

Используемые факты из теоретической

Рис. 26 карты: 4.1; 3.4.

№ 20. В треугольнике АВС на стороне АС как на диаметре построена окружность, пересекающая стороны АВ и АС в точках С₁ и А₁ соответственно. Угол ВАС треугольника АСВ равен 40⁰. Найти угол ВА₁С₁.

План решения.

1. АА₁, СС₁ – высоты ∆АВС.

2. ∆А₁ВС₁ ~ ∆АВС.

3. ÐВА₁С₁.

Ответ: 40⁰.

Используемые факты из теоретической карты: 4.2; 1.

№21. Отрезок АВ есть диаметр круга, а точка С лежит вне этого круга. Отрезки АС и ВС пересекаются с окружностью в точках D и Е соответственно. Найти угол CBD, если площади треугольников DCE и ABC относятся как 1:4.

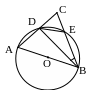План решения.

1. Коэффициент подобия ∆ECD и ∆АСВ.

2. .

3.

Ответ: 30⁰.

Используемые факты из теоретической карты: 4.2; 1.

Рис. 28

№22. В остроугольном треугольнике АВС проведены высоты АА₁ и СС₁, пересекающиеся в точке Н. Вокруг треугольника ВНА₁ описана окружность. Мера дуги ВА₁ равна 60⁰. Найти меру угла АСВ треугольника АВС.

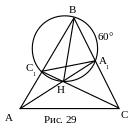
План решения.

1. Центр данной окружность принадлежит ВН.

2. Точка С₁ лежит на данной окружности.

3. ∆ А₁ВС₁ ~ ∆ АВС.

4.

5.

Ответ: 30⁰.

Используемые факты из теоретической карты: 4.2.

№23. Длина основания равнобедренного треугольника равна 12 см, а боковой стороны 18 см. К боковым сторонам треугольника проведены высоты. Вычислить длину отрезка, концы которого совпадают с основаниями высот.

П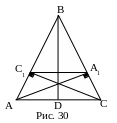 лан решения.

1. ∆А₁ВС₁ ~ ∆АВС

2. .

3. А₁С₁.

Ответ: .

Используемые факты из теоретической карты: 4.2.

№24. Доказать, что высоты остроугольного треугольника являются биссектрисами его ортоцентрического треугольника. (Ортоцентрическим называется треугольник, вершинами которого являются основания высот данного треугольника).

План решения.

1. ∆А₁В С₁~ ∆АВС

2.

3. ∆А₁В₁С ~ ∆АВС

4.

5.

Используемые факты из теоретической карты: 4.2;1.

№25. В остроугольном треугольнике АВС из вершин А и С на стороны ВС и АВ опущены высоты АР и CQ. Вычислить длину стороны АС, если известно, что периметр треугольника АВС равен 15, периметр треугольника BPQ равен 9, а радиус окружности, описанной около треугольника BPQ равен .

П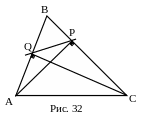 лан решения.

1. ∆PBQ ~ ∆АВС.

2. Коэффициент подобия.

B

3. Радиус окружности,

описанной около ∆АВС.

4. cosB, sinB.

5. AC.

Ответ: 4,8.

Используемые факты из теоретической карты: 4.2; 3.5; 3.6

№26. Стороны треугольника равны 28 см, 32 см, 36 см. Определить периметр ортоцентрического треугольника.

П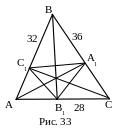 лан решения.

1. cos В, cos C, cos A.

2. А₁В₁, В₁С₁, А₁С₁.

3. Р . Ответ: 45 см.

Используемые факты из теоретической

карты: 4.2; 3.6.

№27. В треугольнике ABC на средней линии DE, параллельной AB, как на диаметре построена окружность, пересекающая стороны AC и BC в точках M и N. Найти MN, если BC=a, AC=b, AB=c.

П

С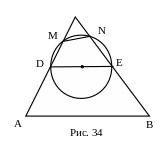

лан решения.

1. ∆ NMC ~ ∆ АВС.

2. Коэффициент подобия, равный соsС.

3. MN.

Ответ:

Используемые факты из теоретической карты: 4.2.